Latent space analysis and generalization to out-of-distribution data

Understanding the relationships between data points in the latent decision space derived by the deep learning system is critical to evaluating and interpreting the performance of the system on real world data. Detecting \textit{out-of-distribution} (OOD) data for deep learning systems continues to be an active research topic. We investigate the connection between latent space OOD detection and classification accuracy of the model. Using open source simulated and measured Synthetic Aperture RADAR (SAR) datasets, we empirically demonstrate that the OOD detection cannot be used as a proxy measure for model performance. We hope to inspire additional research into the geometric properties of the latent space that may yield future insights into deep learning robustness and generalizability.

Out-of-Distribution Learning with Human Feedback

Out-of-distribution (OOD) learning often relies heavily on statistical approaches or predefined assumptions about OOD data distributions, hindering their efficacy in addressing multifaceted challenges of OOD generalization and OOD detection in real-world deployment environments. This paper presents a novel framework for OOD learning with human feedback, which can provide invaluable insights into the nature of OOD shifts and guide effective model adaptation. Our framework capitalizes on the freely available unlabeled data in the wild that captures the environmental test-time OOD distributions under both covariate and semantic shifts. To harness such data, our key idea is to selectively provide human feedback and label a small number of informative samples from the wild data distribution, which are then used to train a multi-class classifier and an OOD detector. By exploiting human feedback, we enhance the robustness and reliability of machine learning models, equipping them with the capability to handle OOD scenarios with greater precision. We provide theoretical insights on the generalization error bounds to justify our algorithm. Extensive experiments show the superiority of our method, outperforming the current state-of-the-art by a significant margin.

Characterizing Inter-Layer Functional Mappings of Deep Learning Models

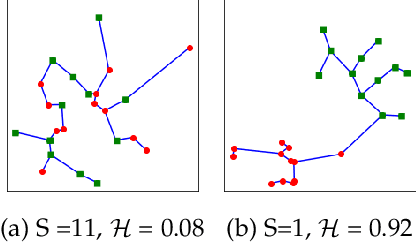
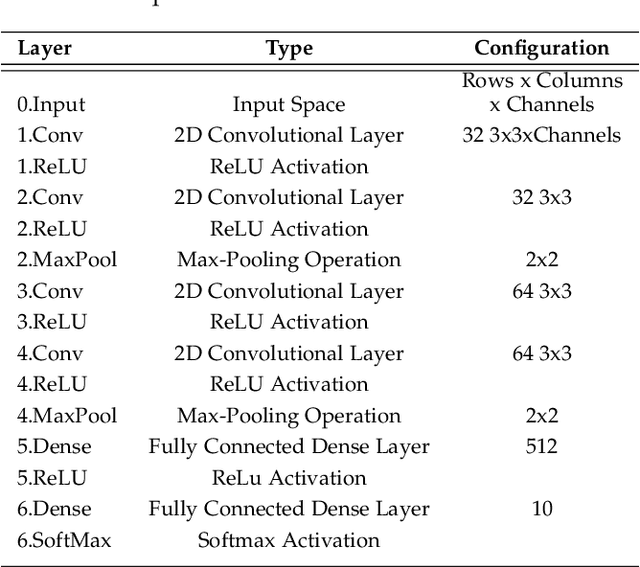
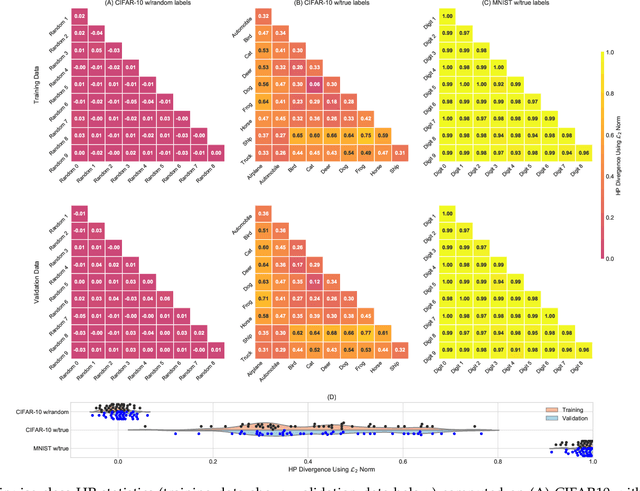
Deep learning architectures have demonstrated state-of-the-art performance for object classification and have become ubiquitous in commercial products. These methods are often applied without understanding (a) the difficulty of a classification task given the input data, and (b) how a specific deep learning architecture transforms that data. To answer (a) and (b), we illustrate the utility of a multivariate nonparametric estimator of class separation, the Henze-Penrose (HP) statistic, in the original as well as layer-induced representations. Given an $N$-class problem, our contribution defines the $C(N,2)$ combinations of HP statistics as a sample from a distribution of class-pair separations. This allows us to characterize the distributional change to class separation induced at each layer of the model. Fisher permutation tests are used to detect statistically significant changes within a model. By comparing the HP statistic distributions between layers, one can statistically characterize: layer adaptation during training, the contribution of each layer to the classification task, and the presence or absence of consistency between training and validation data. This is demonstrated for a simple deep neural network using CIFAR10 with random-labels, CIFAR10, and MNIST datasets.