Latent space analysis and generalization to out-of-distribution data

Understanding the relationships between data points in the latent decision space derived by the deep learning system is critical to evaluating and interpreting the performance of the system on real world data. Detecting \textit{out-of-distribution} (OOD) data for deep learning systems continues to be an active research topic. We investigate the connection between latent space OOD detection and classification accuracy of the model. Using open source simulated and measured Synthetic Aperture RADAR (SAR) datasets, we empirically demonstrate that the OOD detection cannot be used as a proxy measure for model performance. We hope to inspire additional research into the geometric properties of the latent space that may yield future insights into deep learning robustness and generalizability.

Characterizing Inter-Layer Functional Mappings of Deep Learning Models

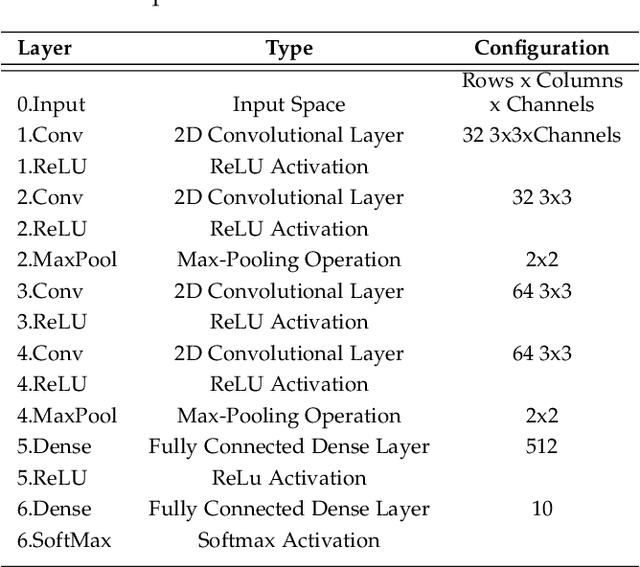
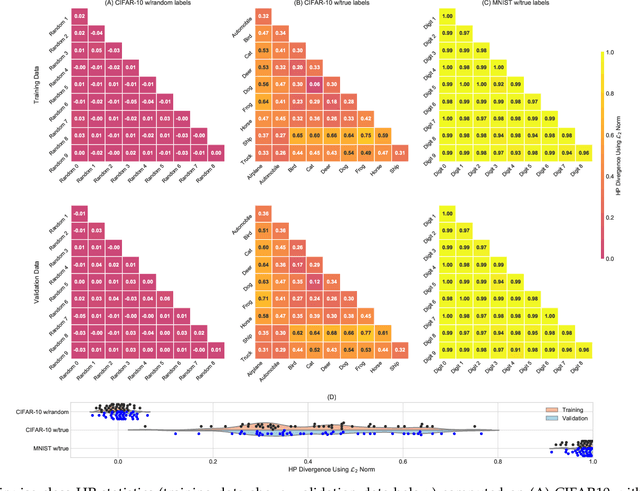
Deep learning architectures have demonstrated state-of-the-art performance for object classification and have become ubiquitous in commercial products. These methods are often applied without understanding (a) the difficulty of a classification task given the input data, and (b) how a specific deep learning architecture transforms that data. To answer (a) and (b), we illustrate the utility of a multivariate nonparametric estimator of class separation, the Henze-Penrose (HP) statistic, in the original as well as layer-induced representations. Given an $N$-class problem, our contribution defines the $C(N,2)$ combinations of HP statistics as a sample from a distribution of class-pair separations. This allows us to characterize the distributional change to class separation induced at each layer of the model. Fisher permutation tests are used to detect statistically significant changes within a model. By comparing the HP statistic distributions between layers, one can statistically characterize: layer adaptation during training, the contribution of each layer to the classification task, and the presence or absence of consistency between training and validation data. This is demonstrated for a simple deep neural network using CIFAR10 with random-labels, CIFAR10, and MNIST datasets.

A formally verified proof of the prime number theorem

The prime number theorem, established by Hadamard and de la Vall'ee Poussin independently in 1896, asserts that the density of primes in the positive integers is asymptotic to 1 / ln x. Whereas their proofs made serious use of the methods of complex analysis, elementary proofs were provided by Selberg and Erd"os in 1948. We describe a formally verified version of Selberg's proof, obtained using the Isabelle proof assistant.