On the symmetries in the dynamics of wide two-layer neural networks

We consider the idealized setting of gradient flow on the population risk for infinitely wide two-layer ReLU neural networks (without bias), and study the effect of symmetries on the learned parameters and predictors. We first describe a general class of symmetries which, when satisfied by the target function $f^*$ and the input distribution, are preserved by the dynamics. We then study more specific cases. When $f^*$ is odd, we show that the dynamics of the predictor reduces to that of a (non-linearly parameterized) linear predictor, and its exponential convergence can be guaranteed. When $f^*$ has a low-dimensional structure, we prove that the gradient flow PDE reduces to a lower-dimensional PDE. Furthermore, we present informal and numerical arguments that suggest that the input neurons align with the lower-dimensional structure of the problem.

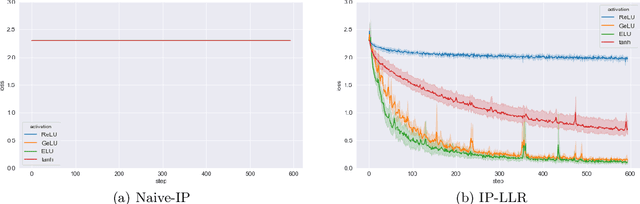
Training Integrable Parameterizations of Deep Neural Networks in the Infinite-Width Limit

To theoretically understand the behavior of trained deep neural networks, it is necessary to study the dynamics induced by gradient methods from a random initialization. However, the nonlinear and compositional structure of these models make these dynamics difficult to analyze. To overcome these challenges, large-width asymptotics have recently emerged as a fruitful viewpoint and led to practical insights on real-world deep networks. For two-layer neural networks, it has been understood via these asymptotics that the nature of the trained model radically changes depending on the scale of the initial random weights, ranging from a kernel regime (for large initial variance) to a feature learning regime (for small initial variance). For deeper networks more regimes are possible, and in this paper we study in detail a specific choice of "small" initialization corresponding to ''mean-field'' limits of neural networks, which we call integrable parameterizations (IPs). First, we show that under standard i.i.d. zero-mean initialization, integrable parameterizations of neural networks with more than four layers start at a stationary point in the infinite-width limit and no learning occurs. We then propose various methods to avoid this trivial behavior and analyze in detail the resulting dynamics. In particular, one of these methods consists in using large initial learning rates, and we show that it is equivalent to a modification of the recently proposed maximal update parameterization $\mu$P. We confirm our results with numerical experiments on image classification tasks, which additionally show a strong difference in behavior between various choices of activation functions that is not yet captured by theory.

SizeFlags: Reducing Size and Fit Related Returns in Fashion E-Commerce

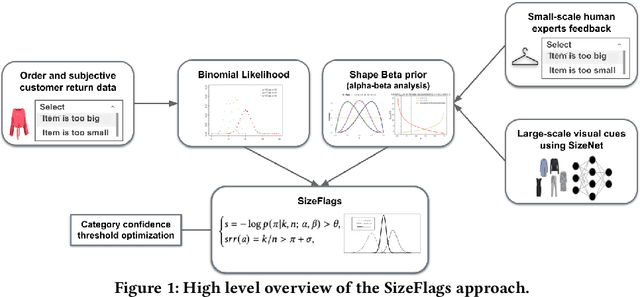
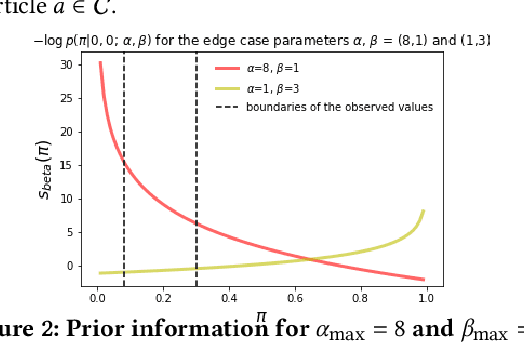
E-commerce is growing at an unprecedented rate and the fashion industry has recently witnessed a noticeable shift in customers' order behaviour towards stronger online shopping. However, fashion articles ordered online do not always find their way to a customer's wardrobe. In fact, a large share of them end up being returned. Finding clothes that fit online is very challenging and accounts for one of the main drivers of increased return rates in fashion e-commerce. Size and fit related returns severely impact 1. the customers experience and their dissatisfaction with online shopping, 2. the environment through an increased carbon footprint, and 3. the profitability of online fashion platforms. Due to poor fit, customers often end up returning articles that they like but do not fit them, which they have to re-order in a different size. To tackle this issue we introduce SizeFlags, a probabilistic Bayesian model based on weakly annotated large-scale data from customers. Leveraging the advantages of the Bayesian framework, we extend our model to successfully integrate rich priors from human experts feedback and computer vision intelligence. Through extensive experimentation, large-scale A/B testing and continuous evaluation of the model in production, we demonstrate the strong impact of the proposed approach in robustly reducing size-related returns in online fashion over 14 countries.

Ranked Reward: Enabling Self-Play Reinforcement Learning for Combinatorial Optimization

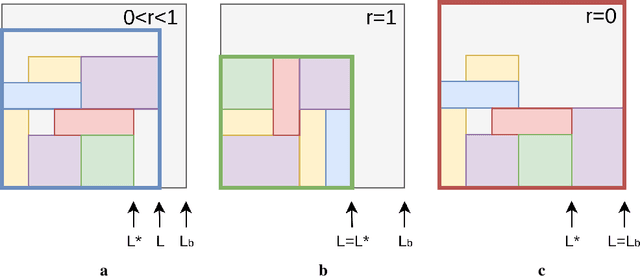
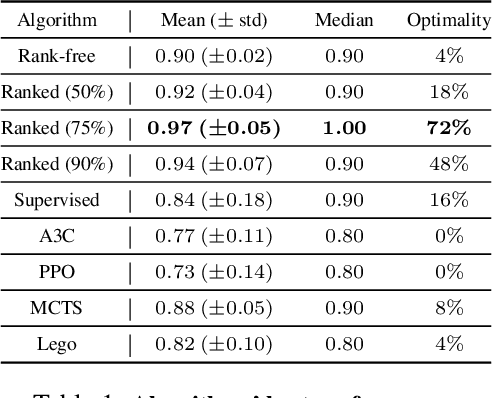
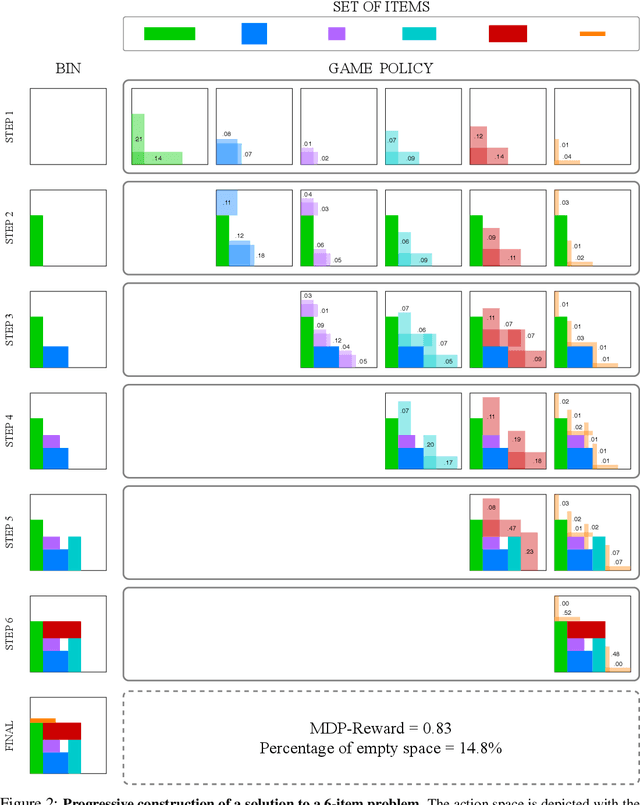
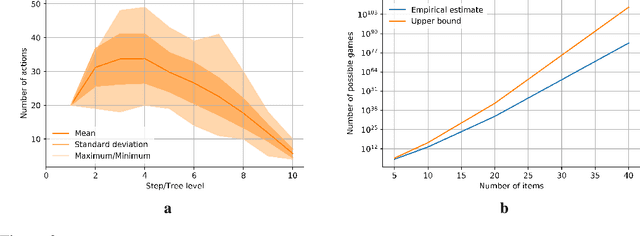
Adversarial self-play in two-player games has delivered impressive results when used with reinforcement learning algorithms that combine deep neural networks and tree search. Algorithms like AlphaZero and Expert Iteration learn tabula-rasa, producing highly informative training data on the fly. However, the self-play training strategy is not directly applicable to single-player games. Recently, several practically important combinatorial optimization problems, such as the traveling salesman problem and the bin packing problem, have been reformulated as reinforcement learning problems, increasing the importance of enabling the benefits of self-play beyond two-player games. We present the Ranked Reward (R2) algorithm which accomplishes this by ranking the rewards obtained by a single agent over multiple games to create a relative performance metric. Results from applying the R2 algorithm to instances of a two-dimensional bin packing problem show that it outperforms generic Monte Carlo tree search, heuristic algorithms and reinforcement learning algorithms not using ranked rewards.