Composable Function-preserving Expansions for Transformer Architectures

Training state-of-the-art neural networks requires a high cost in terms of compute and time. Model scale is recognized to be a critical factor to achieve and improve the state-of-the-art. Increasing the scale of a neural network normally requires restarting from scratch by randomly initializing all the parameters of the model, as this implies a change of architecture's parameters that does not allow for a straightforward transfer of knowledge from smaller size models. In this work, we propose six composable transformations to incrementally increase the size of transformer-based neural networks while preserving functionality, allowing to expand the capacity of the model as needed. We provide proof of exact function preservation under minimal initialization constraints for each transformation. The proposed methods may enable efficient training pipelines for larger and more powerful models by progressively expanding the architecture throughout training.

Architectural Optimization over Subgroups for Equivariant Neural Networks

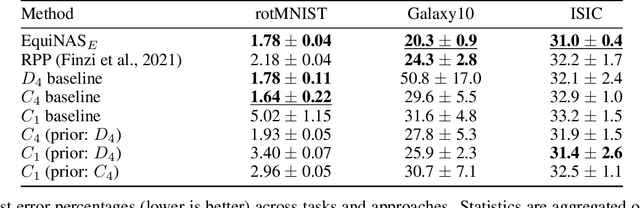
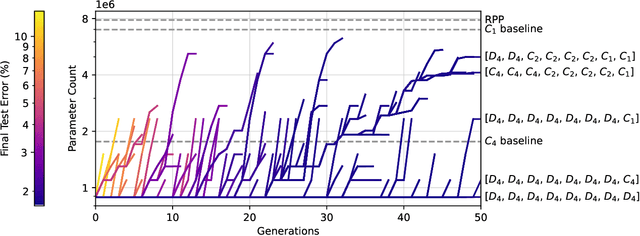
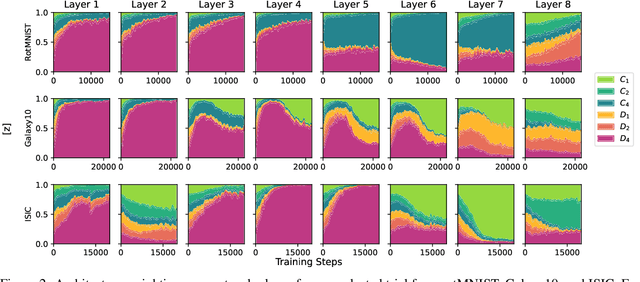
Incorporating equivariance to symmetry groups as a constraint during neural network training can improve performance and generalization for tasks exhibiting those symmetries, but such symmetries are often not perfectly nor explicitly present. This motivates algorithmically optimizing the architectural constraints imposed by equivariance. We propose the equivariance relaxation morphism, which preserves functionality while reparameterizing a group equivariant layer to operate with equivariance constraints on a subgroup, as well as the $[G]$-mixed equivariant layer, which mixes layers constrained to different groups to enable within-layer equivariance optimization. We further present evolutionary and differentiable neural architecture search (NAS) algorithms that utilize these mechanisms respectively for equivariance-aware architectural optimization. Experiments across a variety of datasets show the benefit of dynamically constrained equivariance to find effective architectures with approximate equivariance.

When, where, and how to add new neurons to ANNs

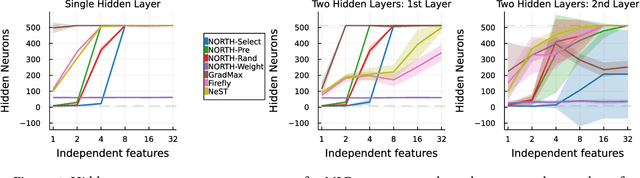
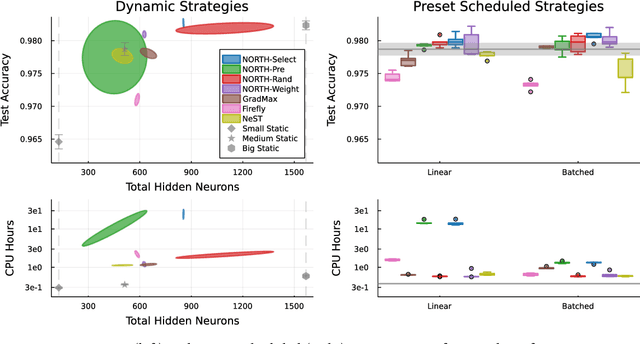
Neurogenesis in ANNs is an understudied and difficult problem, even compared to other forms of structural learning like pruning. By decomposing it into triggers and initializations, we introduce a framework for studying the various facets of neurogenesis: when, where, and how to add neurons during the learning process. We present the Neural Orthogonality (NORTH*) suite of neurogenesis strategies, combining layer-wise triggers and initializations based on the orthogonality of activations or weights to dynamically grow performant networks that converge to an efficient size. We evaluate our contributions against other recent neurogenesis works with MLPs.

On Constrained Optimization in Differentiable Neural Architecture Search

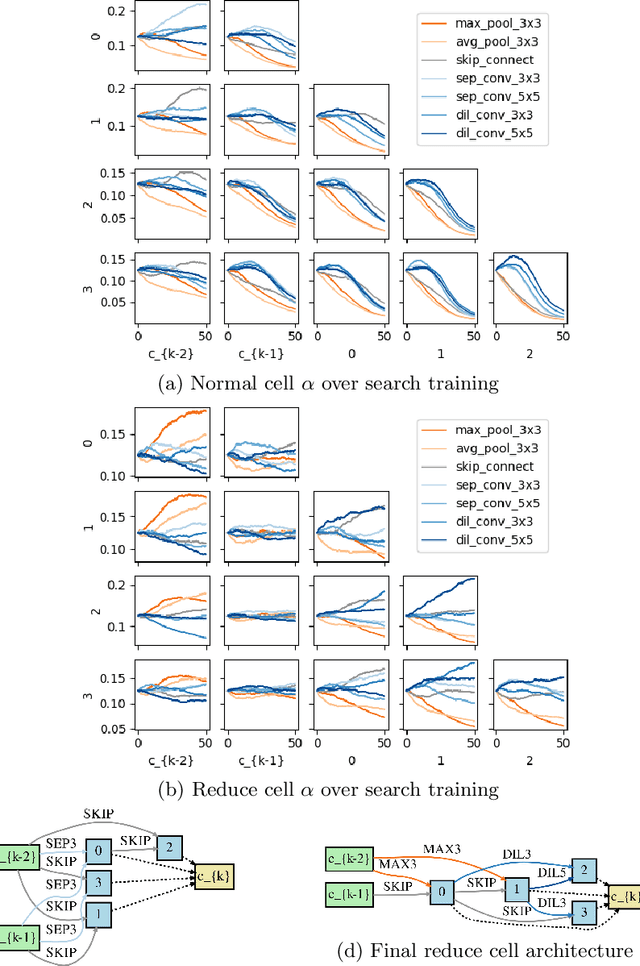
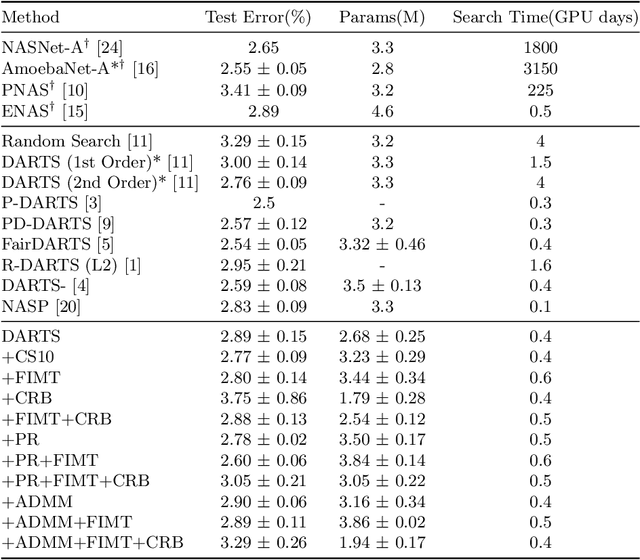
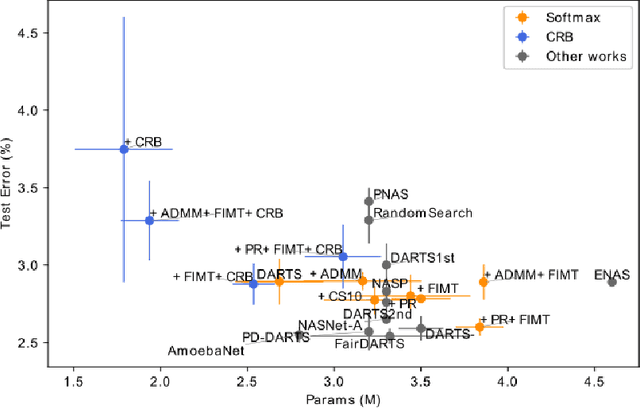
Differentiable Architecture Search (DARTS) is a recently proposed neural architecture search (NAS) method based on a differentiable relaxation. Due to its success, numerous variants analyzing and improving parts of the DARTS framework have recently been proposed. By considering the problem as a constrained bilevel optimization, we propose and analyze three improvements to architectural weight competition, update scheduling, and regularization towards discretization. First, we introduce a new approach to the activation of architecture weights, which prevents confounding competition within an edge and allows for fair comparison across edges to aid in discretization. Next, we propose a dynamic schedule based on per-minibatch network information to make architecture updates more informed. Finally, we consider two regularizations, based on proximity to discretization and the Alternating Directions Method of Multipliers (ADMM) algorithm, to promote early discretization. Our results show that this new activation scheme reduces final architecture size and the regularizations improve reliability in search results while maintaining comparable performance to state-of-the-art in NAS, especially when used with our new dynamic informed schedule.