Architectural Optimization over Subgroups for Equivariant Neural Networks

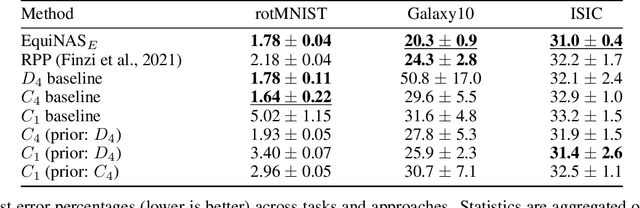
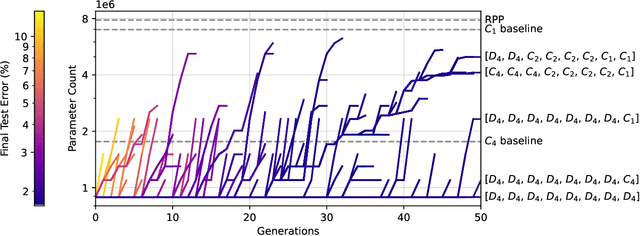
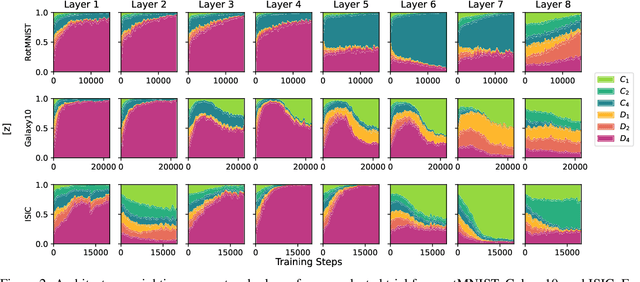
Incorporating equivariance to symmetry groups as a constraint during neural network training can improve performance and generalization for tasks exhibiting those symmetries, but such symmetries are often not perfectly nor explicitly present. This motivates algorithmically optimizing the architectural constraints imposed by equivariance. We propose the equivariance relaxation morphism, which preserves functionality while reparameterizing a group equivariant layer to operate with equivariance constraints on a subgroup, as well as the $[G]$-mixed equivariant layer, which mixes layers constrained to different groups to enable within-layer equivariance optimization. We further present evolutionary and differentiable neural architecture search (NAS) algorithms that utilize these mechanisms respectively for equivariance-aware architectural optimization. Experiments across a variety of datasets show the benefit of dynamically constrained equivariance to find effective architectures with approximate equivariance.