Neural Functional Transformers

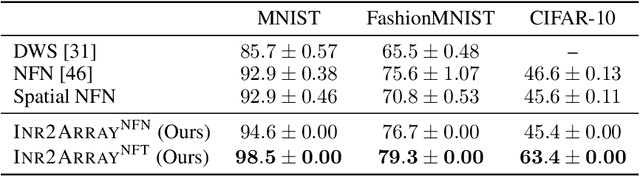
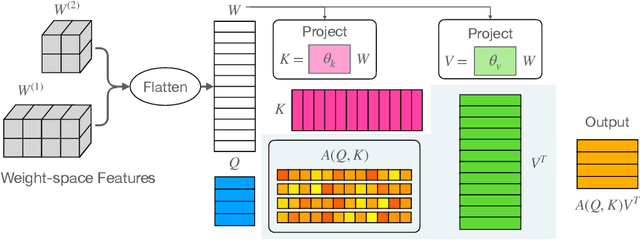
The recent success of neural networks as implicit representation of data has driven growing interest in neural functionals: models that can process other neural networks as input by operating directly over their weight spaces. Nevertheless, constructing expressive and efficient neural functional architectures that can handle high-dimensional weight-space objects remains challenging. This paper uses the attention mechanism to define a novel set of permutation equivariant weight-space layers and composes them into deep equivariant models called neural functional Transformers (NFTs). NFTs respect weight-space permutation symmetries while incorporating the advantages of attention, which have exhibited remarkable success across multiple domains. In experiments processing the weights of feedforward MLPs and CNNs, we find that NFTs match or exceed the performance of prior weight-space methods. We also leverage NFTs to develop Inr2Array, a novel method for computing permutation invariant latent representations from the weights of implicit neural representations (INRs). Our proposed method improves INR classification accuracy by up to $+17\%$ over existing methods. We provide an implementation of our layers at https://github.com/AllanYangZhou/nfn.

Permutation Equivariant Neural Functionals

This work studies the design of neural networks that can process the weights or gradients of other neural networks, which we refer to as neural functional networks (NFNs). Despite a wide range of potential applications, including learned optimization, processing implicit neural representations, network editing, and policy evaluation, there are few unifying principles for designing effective architectures that process the weights of other networks. We approach the design of neural functionals through the lens of symmetry, in particular by focusing on the permutation symmetries that arise in the weights of deep feedforward networks because hidden layer neurons have no inherent order. We introduce a framework for building permutation equivariant neural functionals, whose architectures encode these symmetries as an inductive bias. The key building blocks of this framework are NF-Layers (neural functional layers) that we constrain to be permutation equivariant through an appropriate parameter sharing scheme. In our experiments, we find that permutation equivariant neural functionals are effective on a diverse set of tasks that require processing the weights of MLPs and CNNs, such as predicting classifier generalization, producing "winning ticket" sparsity masks for initializations, and editing the weights of implicit neural representations (INRs). In addition, we provide code for our models and experiments at https://github.com/AllanYangZhou/nfn.