Refining Targeted Syntactic Evaluation of Language Models

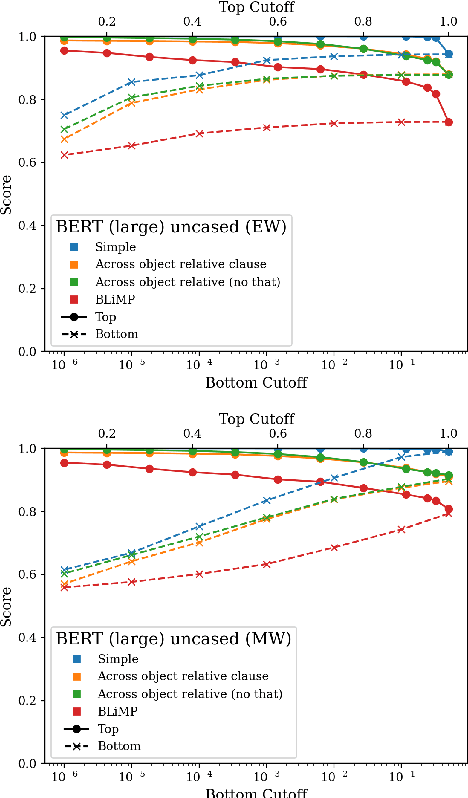
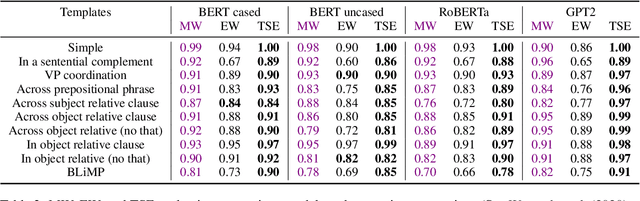
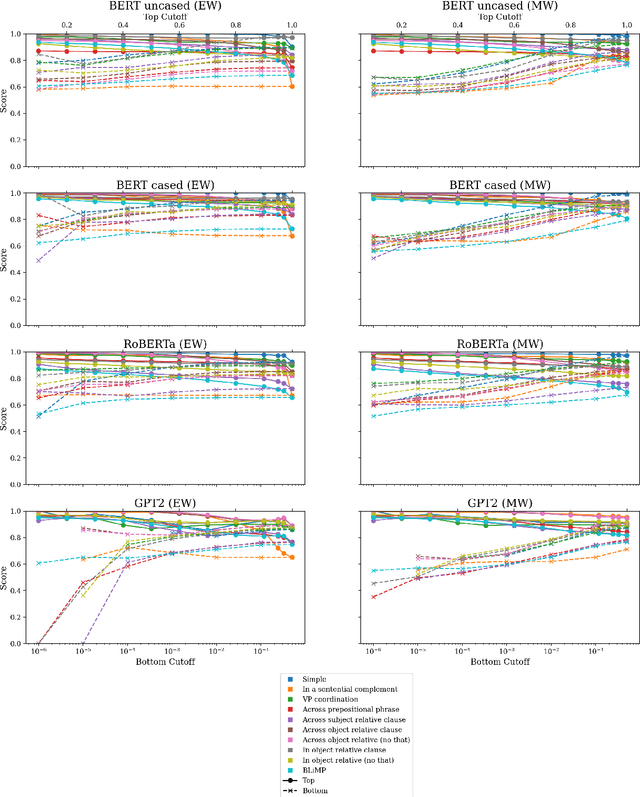
Targeted syntactic evaluation of subject-verb number agreement in English (TSE) evaluates language models' syntactic knowledge using hand-crafted minimal pairs of sentences that differ only in the main verb's conjugation. The method evaluates whether language models rate each grammatical sentence as more likely than its ungrammatical counterpart. We identify two distinct goals for TSE. First, evaluating the systematicity of a language model's syntactic knowledge: given a sentence, can it conjugate arbitrary verbs correctly? Second, evaluating a model's likely behavior: given a sentence, does the model concentrate its probability mass on correctly conjugated verbs, even if only on a subset of the possible verbs? We argue that current implementations of TSE do not directly capture either of these goals, and propose new metrics to capture each goal separately. Under our metrics, we find that TSE overestimates systematicity of language models, but that models score up to 40% better on verbs that they predict are likely in context.

On the Accuracy of Influence Functions for Measuring Group Effects

Influence functions estimate the effect of removing particular training points on a model without needing to retrain it. They are based on a first-order approximation that is accurate for small changes in the model, and so are commonly used for studying the effect of individual points in large datasets. However, we often want to study the effects of large groups of training points, e.g., to diagnose batch effect or apportion credit between different data sources. Removing such large groups can result in significant changes to the model. Are influence functions still accurate in this setting? In this paper, we find that across many different types of groups and in a range of real-world datasets, the influence of a group correlates surprisingly well with its actual effect, even if the absolute and relative error can be large. Our theoretical analysis shows that such correlation arises under certain settings but need not hold in general, indicating that real-world datasets have particular properties that keep the influence approximation well-behaved.