Self-Improving Multilingual Long Reasoning via Translation-Reasoning Integrated Training

Long reasoning models often struggle in multilingual settings: they tend to reason in English for non-English questions; when constrained to reasoning in the question language, accuracies drop substantially. The struggle is caused by the limited abilities for both multilingual question understanding and multilingual reasoning. To address both problems, we propose TRIT (Translation-Reasoning Integrated Training), a self-improving framework that integrates the training of translation into multilingual reasoning. Without external feedback or additional multilingual data, our method jointly enhances multilingual question understanding and response generation. On MMATH, our method outperforms multiple baselines by an average of 7 percentage points, improving both answer correctness and language consistency. Further analysis reveals that integrating translation training improves cross-lingual question alignment by over 10 percentage points and enhances translation quality for both mathematical questions and general-domain text, with gains up to 8.4 COMET points on FLORES-200.

PATS: Process-Level Adaptive Thinking Mode Switching

Current large-language models (LLMs) typically adopt a fixed reasoning strategy, either simple or complex, for all questions, regardless of their difficulty. This neglect of variation in task and reasoning process complexity leads to an imbalance between performance and efficiency. Existing methods attempt to implement training-free fast-slow thinking system switching to handle problems of varying difficulty, but are limited by coarse-grained solution-level strategy adjustments. To address this issue, we propose a novel reasoning paradigm: Process-Level Adaptive Thinking Mode Switching (PATS), which enables LLMs to dynamically adjust their reasoning strategy based on the difficulty of each step, optimizing the balance between accuracy and computational efficiency. Our approach integrates Process Reward Models (PRMs) with Beam Search, incorporating progressive mode switching and bad-step penalty mechanisms. Experiments on diverse mathematical benchmarks demonstrate that our methodology achieves high accuracy while maintaining moderate token usage. This study emphasizes the significance of process-level, difficulty-aware reasoning strategy adaptation, offering valuable insights into efficient inference for LLMs.

R-PRM: Reasoning-Driven Process Reward Modeling

Large language models (LLMs) inevitably make mistakes when performing step-by-step mathematical reasoning. Process Reward Models (PRMs) have emerged as a promising solution by evaluating each reasoning step. However, existing PRMs typically output evaluation scores directly, limiting both learning efficiency and evaluation accuracy, which is further exacerbated by the scarcity of annotated data. To address these issues, we propose Reasoning-Driven Process Reward Modeling (R-PRM). First, we leverage stronger LLMs to generate seed data from limited annotations, effectively bootstrapping our model's reasoning capabilities and enabling comprehensive step-by-step evaluation. Second, we further enhance performance through preference optimization, without requiring additional annotated data. Third, we introduce inference-time scaling to fully harness the model's reasoning potential. Extensive experiments demonstrate R-PRM's effectiveness: on ProcessBench and PRMBench, it surpasses strong baselines by 11.9 and 8.5 points in F1 scores, respectively. When applied to guide mathematical reasoning, R-PRM achieves consistent accuracy improvements of over 8.5 points across six challenging datasets. Further analysis reveals that R-PRM exhibits more comprehensive evaluation and stronger generalization capabilities, thereby highlighting its significant potential.

Process-based Self-Rewarding Language Models

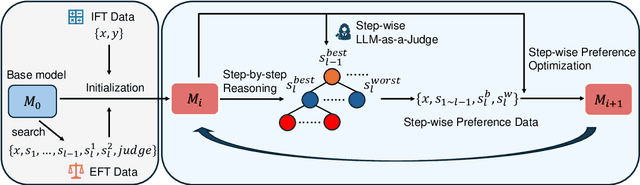
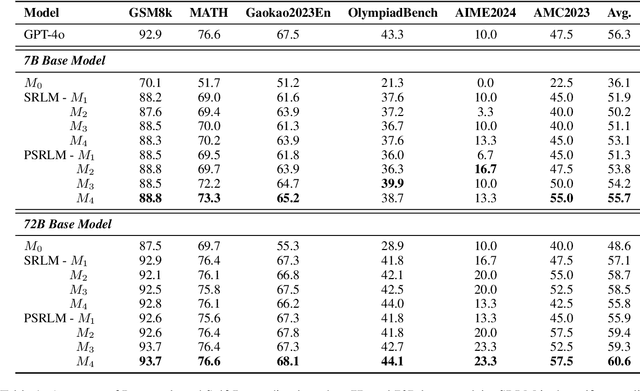
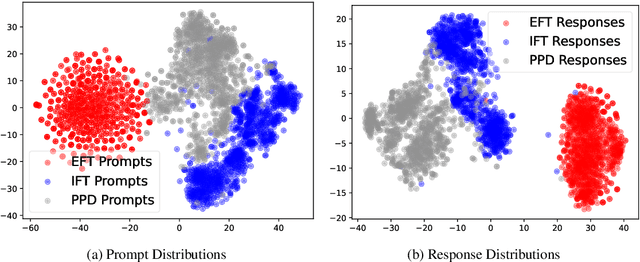
Large Language Models have demonstrated outstanding performance across various downstream tasks and have been widely applied in multiple scenarios. Human-annotated preference data is used for training to further improve LLMs' performance, which is constrained by the upper limit of human performance. Therefore, Self-Rewarding method has been proposed, where LLMs generate training data by rewarding their own outputs. However, the existing self-rewarding paradigm is not effective in mathematical reasoning scenarios and may even lead to a decline in performance. In this work, we propose the Process-based Self-Rewarding pipeline for language models, which introduces long-thought reasoning, step-wise LLM-as-a-Judge, and step-wise preference optimization within the self-rewarding paradigm. Our new paradigm successfully enhances the performance of LLMs on multiple mathematical reasoning benchmarks through iterative Process-based Self-Rewarding, demonstrating the immense potential of self-rewarding to achieve LLM reasoning that may surpass human capabilities.