An optimization-based equilibrium measure describes non-equilibrium steady state dynamics: application to edge of chaos

Understanding neural dynamics is a central topic in machine learning, non-linear physics and neuroscience. However, the dynamics is non-linear, stochastic and particularly non-gradient, i.e., the driving force can not be written as gradient of a potential. These features make analytic studies very challenging. The common tool is to use path integral approach or dynamical mean-field theory, but the drawback is one has to solve the integro-differential or dynamical mean-field equations, which is computationally expensive and has no closed form solutions in general. From the aspect of associated Fokker-Planck equation, the steady state solution is generally unknown. Here, we treat searching for the steady state as an optimization problem, and construct an approximate potential closely related to the speed of the dynamics, and find that searching for the ground state of this potential is equivalent to running a stochastic gradient dynamics. The resultant stationary state follows exactly the canonical Boltzmann measure. Within this framework, the quenched disorder intrinsic in the neural networks can be averaged out by applying the replica method. Our theory reproduces the well-known result of edge-of-chaos, and further the order parameters characterizing the continuous transition are derived, and different scaling behavior with respect to inverse temperature in both sides of the transition is also revealed. Our method opens the door to analytically study the steady state landscape of the deterministic or stochastic high dimensional dynamics.

Meta predictive learning model of natural languages

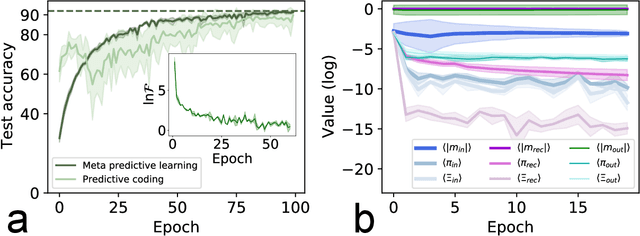
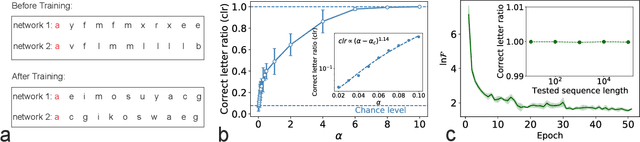
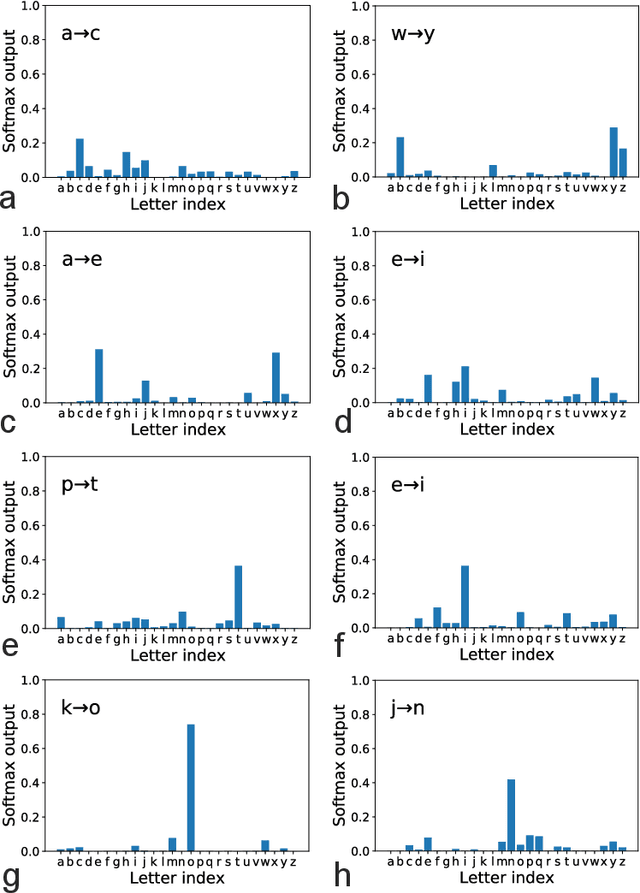
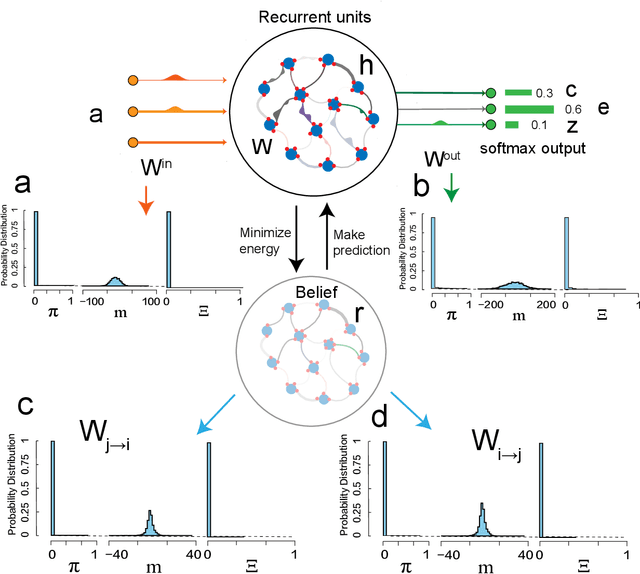
Large language models based on self-attention mechanisms have achieved astonishing performances not only in natural language itself, but also in a variety of tasks of different nature. However, regarding processing language, our human brain may not operate using the same principle. Then, a debate is established on the connection between brain computation and artificial self-supervision adopted in large language models. One of most influential hypothesis in brain computation is the predictive coding framework, which proposes to minimize the prediction error by local learning. However, the role of predictive coding and the associated credit assignment in language processing remains unknown. Here, we propose a mean-field learning model within the predictive coding framework, assuming that the synaptic weight of each connection follows a spike and slab distribution, and only the distribution is trained. This meta predictive learning is successfully validated on classifying handwritten digits where pixels are input to the network in sequence, and on the toy and real language corpus. Our model reveals that most of the connections become deterministic after learning, while the output connections have a higher level of variability. The performance of the resulting network ensemble changes continuously with data load, further improving with more training data, in analogy with the emergent behavior of large language models. Therefore, our model provides a starting point to investigate the physics and biology correspondences of the language processing and the unexpected general intelligence.

Equivalence between algorithmic instability and transition to replica symmetry breaking in perceptron learning systems

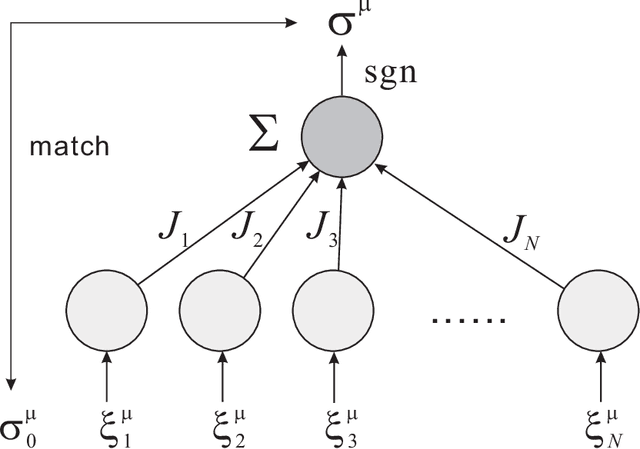
Binary perceptron is a fundamental model of supervised learning for the non-convex optimization, which is a root of the popular deep learning. Binary perceptron is able to achieve a classification of random high-dimensional data by computing the marginal probabilities of binary synapses. The relationship between the algorithmic instability and the equilibrium analysis of the model remains elusive. Here, we establish the relationship by showing that the instability condition around the algorithmic fixed point is identical to the instability for breaking the replica symmetric saddle point solution of the free energy function. Therefore, our analysis provides insights towards bridging the gap between non-convex learning dynamics and statistical mechanics properties of more complex neural networks.