Equivalence between algorithmic instability and transition to replica symmetry breaking in perceptron learning systems
Paper and Code
Nov 26, 2021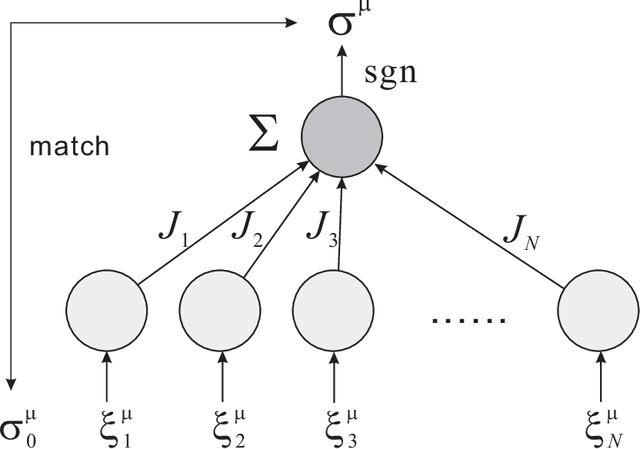
Binary perceptron is a fundamental model of supervised learning for the non-convex optimization, which is a root of the popular deep learning. Binary perceptron is able to achieve a classification of random high-dimensional data by computing the marginal probabilities of binary synapses. The relationship between the algorithmic instability and the equilibrium analysis of the model remains elusive. Here, we establish the relationship by showing that the instability condition around the algorithmic fixed point is identical to the instability for breaking the replica symmetric saddle point solution of the free energy function. Therefore, our analysis provides insights towards bridging the gap between non-convex learning dynamics and statistical mechanics properties of more complex neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge