Performance of orthogonal delay-doppler division multiplexing modulation with imperfect channel estimation

The orthogonal delay-Doppler division multiplexing (ODDM) modulation is a recently proposed multi-carrier modulation that features a realizable pulse orthogonal with respect to the delay-Doppler (DD) plane's fine resolutions. In this paper, we investigate the performance of ODDM systems with imperfect channel estimation considering three detectors, namely the message passing algorithm (MPA) detector, iterative maximum-ratio combining (MRC) detector, and successive interference cancellation with minimum mean square error (SIC-MMSE) detector. We derive the post-equalization signal-to-interference-plus-noise ratio (SINR) for MRC and SIC-MMSE and analyze their bit error rate (BER) performance. Based on this analysis, we propose the MRC with subtractive dither (MRC-SD) and soft SIC-MMSE initialized MRC (SSMI-MRC) detector to improve the BER of iterative MRC. Our results demonstrate that soft SIC-MMSE consistently outperforms the other detectors in BER performance under perfect and imperfect CSI. While MRC exhibits a BER floor above $10^{-5}$, MRC-SD effectively lowers the BER with a negligible increase in detection complexity. SSMI-MRC achieves better BER than hard SIC-MMSE with the same detection complexity order. Additionally, we show that MPA has an error floor and is sensitive to imperfect CSI.

Cross-Validated Tuning of Shrinkage Factors for MVDR Beamforming Based on Regularized Covariance Matrix Estimation

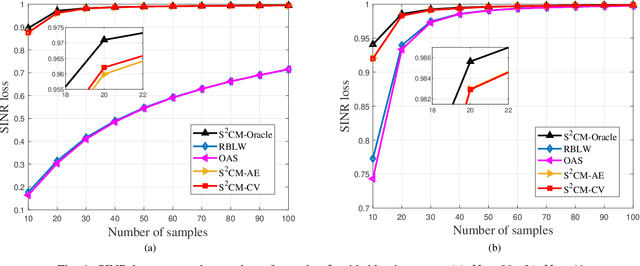
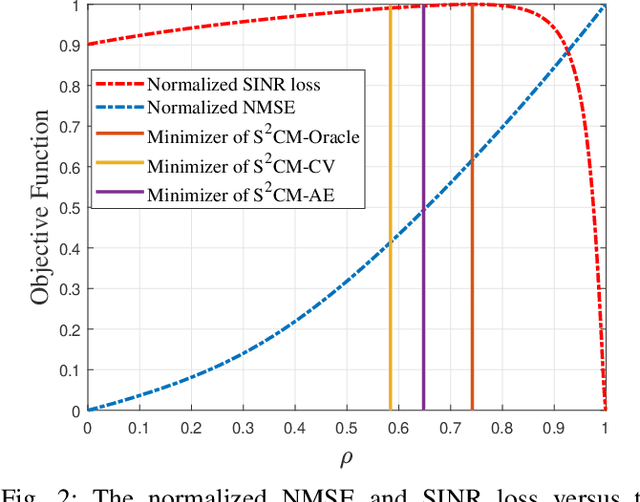
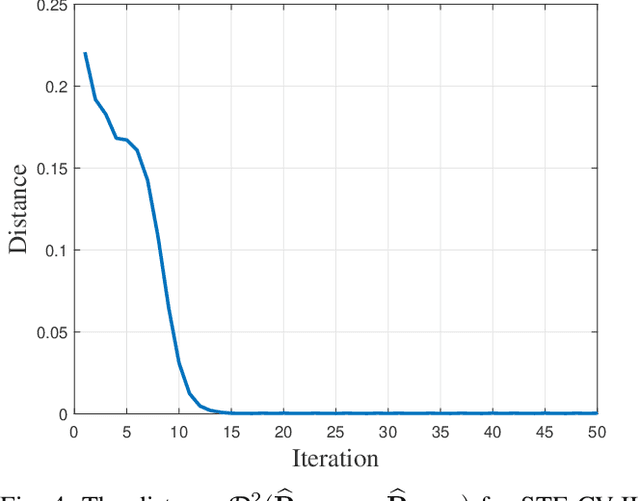
This paper considers the regularized estimation of covariance matrices (CM) of high-dimensional (compound) Gaussian data for minimum variance distortionless response (MVDR) beamforming. Linear shrinkage is applied to improve the accuracy and condition number of the CM estimate for low-sample-support cases. We focus on data-driven techniques that automatically choose the linear shrinkage factors for shrinkage sample covariance matrix ($\text{S}^2$CM) and shrinkage Tyler's estimator (STE) by exploiting cross validation (CV). We propose leave-one-out cross-validation (LOOCV) choices for the shrinkage factors to optimize the beamforming performance, referred to as $\text{S}^2$CM-CV and STE-CV. The (weighted) out-of-sample output power of the beamfomer is chosen as a proxy of the beamformer performance and concise expressions of the LOOCV cost function are derived to allow fast optimization. For the large system regime, asymptotic approximations of the LOOCV cost functions are derived, yielding the $\text{S}^2$CM-AE and STE-AE. In general, the proposed algorithms are able to achieve near-oracle performance in choosing the linear shrinkage factors for MVDR beamforming. Simulation results are provided for validating the proposed methods.

Regularized Estimation of Kronecker-Structured Covariance Matrix

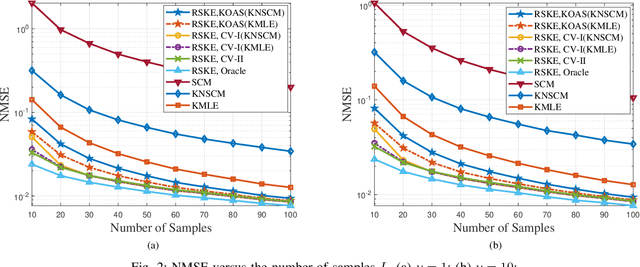
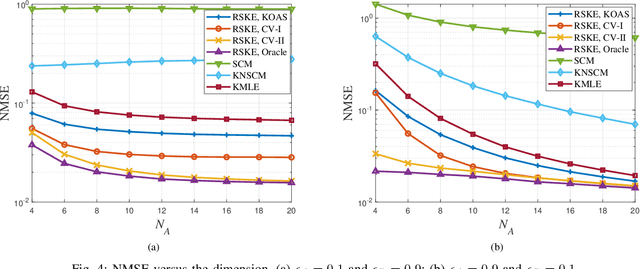
This paper investigates regularized estimation of Kronecker-structured covariance matrices (CM) for complex elliptically symmetric (CES) data. To obtain a well-conditioned estimate of the CM, we add penalty terms of Kullback-Leibler divergence to the negative log-likelihood function of the associated complex angular Gaussian (CAG) distribution. This is shown to be equivalent to regularizing Tyler's fixed-point equations by shrinkage. A sufficient condition that the solution exists is discussed. An iterative algorithm is applied to solve the resulting fixed-point iterations and its convergence is proved. In order to solve the critical problem of tuning the shrinkage factors, we then introduce three methods by exploiting oracle approximating shrinkage (OAS) and cross-validation (CV). When the training samples are limited, the proposed estimator, referred to as the robust shrinkage Kronecker estimator (RSKE), has better performance compared with several existing methods. Simulations are conducted for validating the proposed estimator and demonstrating its high performance.