Manifold Optimization Methods for Hybrid beamforming in mmWave Dual-Function Radar-Communication System

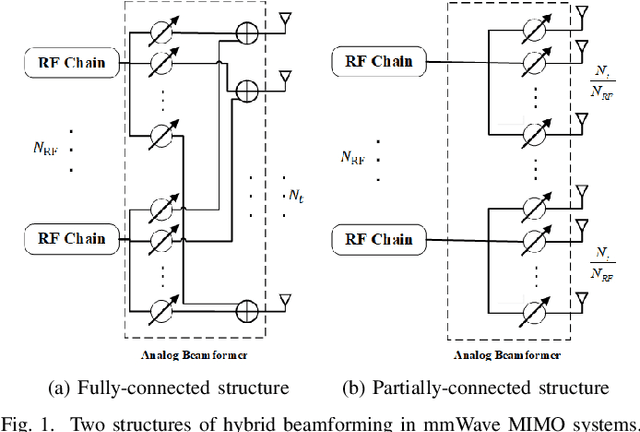
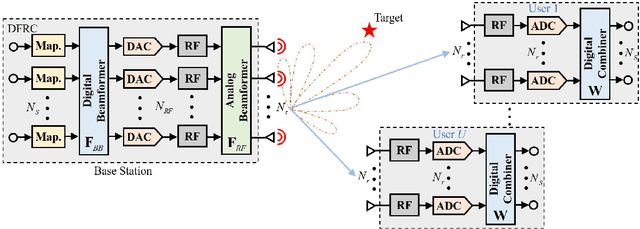
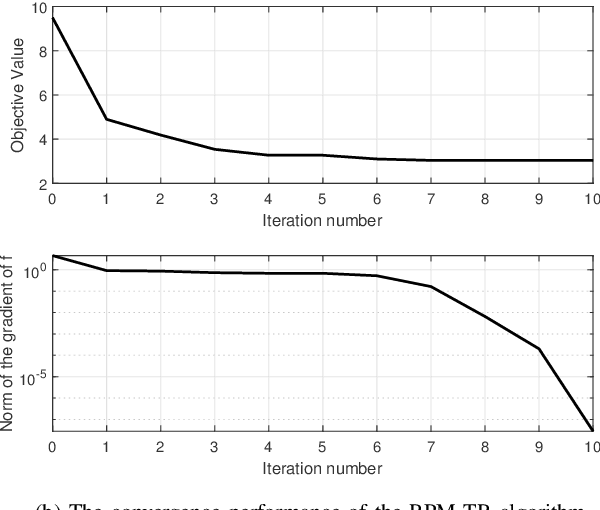
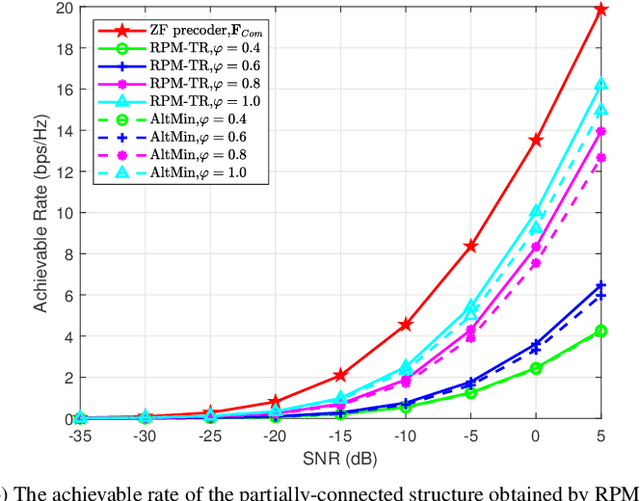
As a cost-effective alternative, hybrid analog and digital beamforming architecture is a promising scheme for millimeter wave (mmWave) system. This paper considers two hybrid beamforming architectures, i.e. the partially-connected and fully-connected structures, for mmWave dual-function radar communication (DFRC) system, where the transmitter communicates with the downlink users and detects radar targets simultaneously. The optimization problems are formulated by minimizing a weighted summation of radar and communication performance, subject to constant modulus and power constraints. To tackle the non-convexities caused by the two resultant problems, effective Riemannian optimization algorithms are proposed. Specifically, for the fully-connected structure, a manifold algorithm based on the alternating direction method of multipliers (ADMM) is developed. While for the partially-connected structure, a low-complexity Riemannian product manifold trust region (RPM-TR) algorithm is proposed to approach the near-optional solution. Numerical simulations are provided to demonstrate the effectiveness of the proposed methods.

Joint Design of Transmit Waveform and Receive Filter for MIMO Radar with One-Bit DACs/ADCs

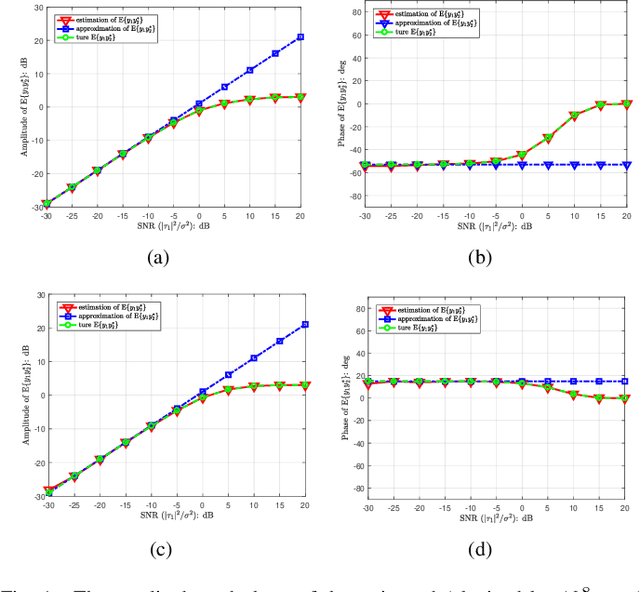
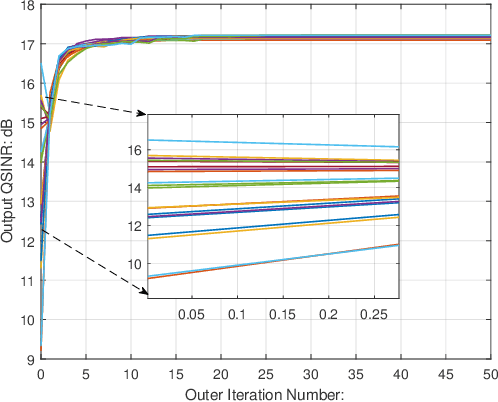
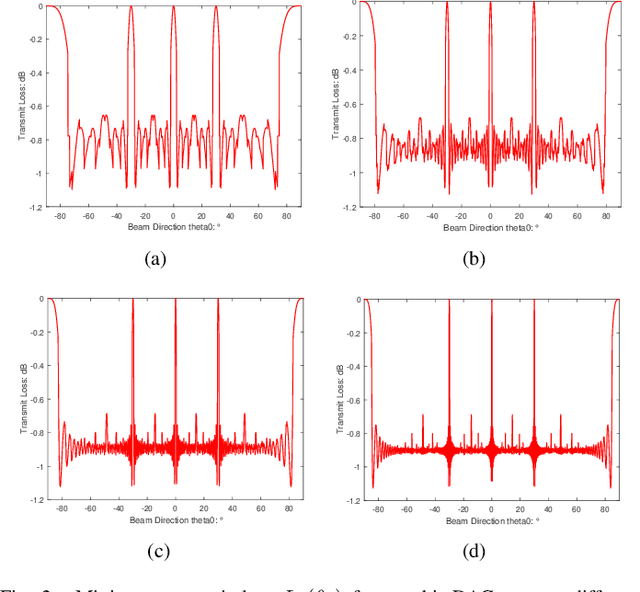
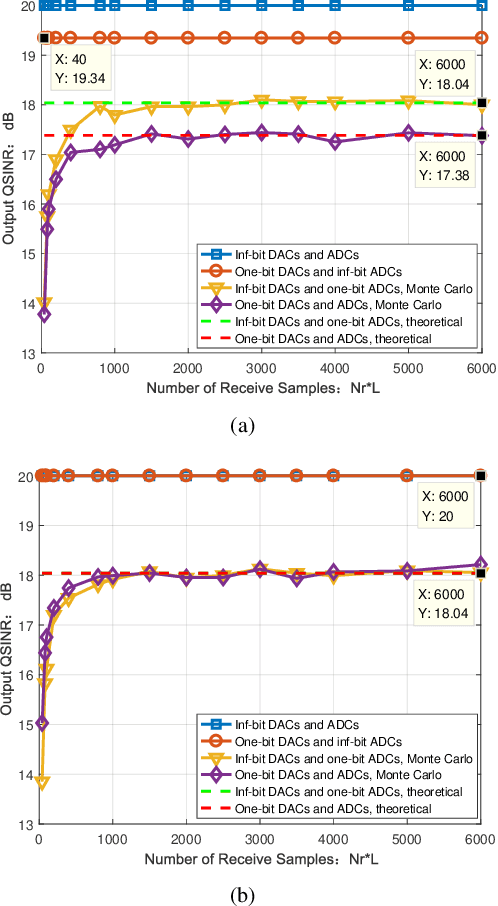
Adopting extremely low-resolution (e.g. one-bit) analog-to-digital converters (ADCs) and digital-to-analog converters (DACs) is able to bring a remarkable saving of low-cost and circuit power for multiple-input multiple-output (MIMO) radar.In this paper, the problem of joint design of transmit waveform and receive filter for collocated MIMO radar with a architecture of one-bit ADCs and DACs is investigated. Under this architecture, we derive the output quantized signal-to-interference-plus-noise ratio (QSINR), which is relative to the detection performance of target, in the presence of signal-dependent interference. The optimization problem is formulated by maximizing the QSINR with a binary waveform constraint. Due to the nonconvex objective and binary constraint, the resulting problem is hard to be directly solved. To this end, we propose an alternating minimization algorithm. More concretely, at each iteration, the closed-form solution of the receive filter is attained by exploiting the minimum variance distortionless response (MVDR) method, and then the one-bit waveform is optimized with the aid of the alternating direction method of multipliers (ADMM) algorithm. In addition, the performance gap between the one-bit MIMO radar and infinite-bit MIMO radar is theoretically analyzed under the noise-only case. Several numerical simulations are provided to demonstrate the effectiveness of the proposed methods.

Cross-Validated Tuning of Shrinkage Factors for MVDR Beamforming Based on Regularized Covariance Matrix Estimation

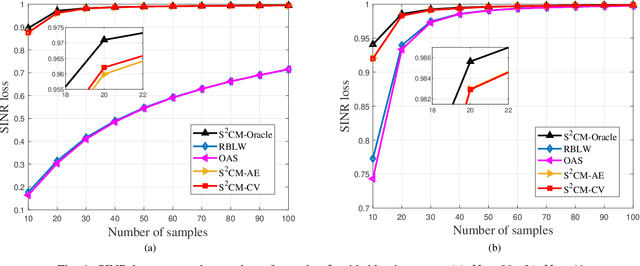
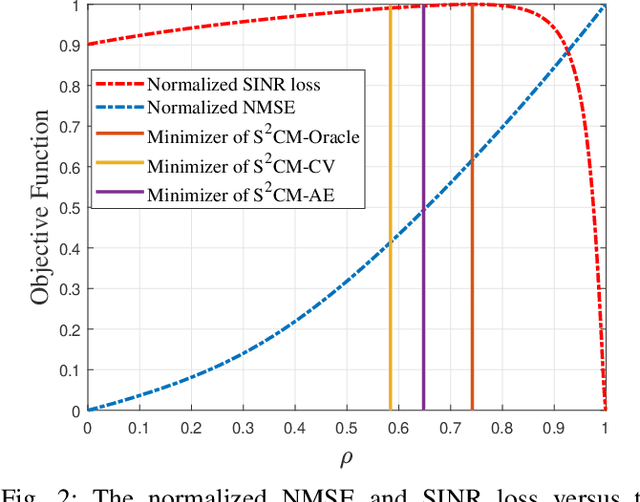
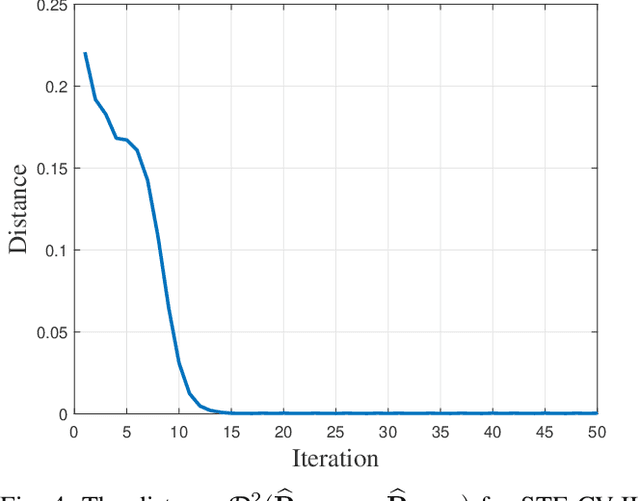
This paper considers the regularized estimation of covariance matrices (CM) of high-dimensional (compound) Gaussian data for minimum variance distortionless response (MVDR) beamforming. Linear shrinkage is applied to improve the accuracy and condition number of the CM estimate for low-sample-support cases. We focus on data-driven techniques that automatically choose the linear shrinkage factors for shrinkage sample covariance matrix ($\text{S}^2$CM) and shrinkage Tyler's estimator (STE) by exploiting cross validation (CV). We propose leave-one-out cross-validation (LOOCV) choices for the shrinkage factors to optimize the beamforming performance, referred to as $\text{S}^2$CM-CV and STE-CV. The (weighted) out-of-sample output power of the beamfomer is chosen as a proxy of the beamformer performance and concise expressions of the LOOCV cost function are derived to allow fast optimization. For the large system regime, asymptotic approximations of the LOOCV cost functions are derived, yielding the $\text{S}^2$CM-AE and STE-AE. In general, the proposed algorithms are able to achieve near-oracle performance in choosing the linear shrinkage factors for MVDR beamforming. Simulation results are provided for validating the proposed methods.

Regularized Estimation of Kronecker-Structured Covariance Matrix

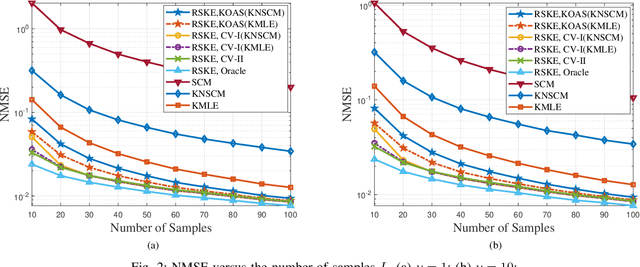
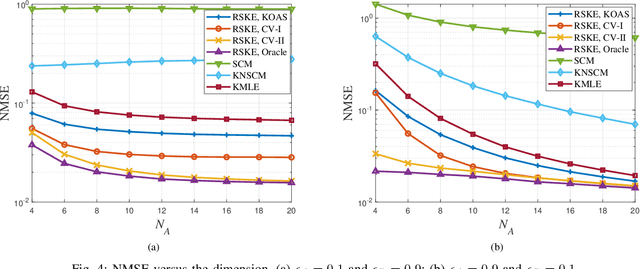
This paper investigates regularized estimation of Kronecker-structured covariance matrices (CM) for complex elliptically symmetric (CES) data. To obtain a well-conditioned estimate of the CM, we add penalty terms of Kullback-Leibler divergence to the negative log-likelihood function of the associated complex angular Gaussian (CAG) distribution. This is shown to be equivalent to regularizing Tyler's fixed-point equations by shrinkage. A sufficient condition that the solution exists is discussed. An iterative algorithm is applied to solve the resulting fixed-point iterations and its convergence is proved. In order to solve the critical problem of tuning the shrinkage factors, we then introduce three methods by exploiting oracle approximating shrinkage (OAS) and cross-validation (CV). When the training samples are limited, the proposed estimator, referred to as the robust shrinkage Kronecker estimator (RSKE), has better performance compared with several existing methods. Simulations are conducted for validating the proposed estimator and demonstrating its high performance.