Cross-Validated Tuning of Shrinkage Factors for MVDR Beamforming Based on Regularized Covariance Matrix Estimation

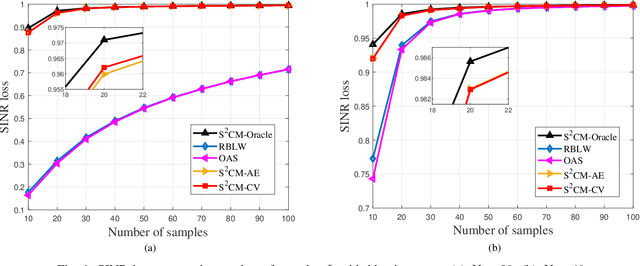
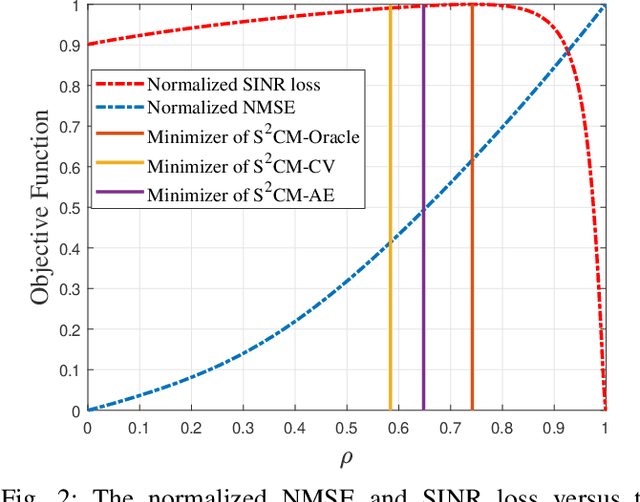
This paper considers the regularized estimation of covariance matrices (CM) of high-dimensional (compound) Gaussian data for minimum variance distortionless response (MVDR) beamforming. Linear shrinkage is applied to improve the accuracy and condition number of the CM estimate for low-sample-support cases. We focus on data-driven techniques that automatically choose the linear shrinkage factors for shrinkage sample covariance matrix ($\text{S}^2$CM) and shrinkage Tyler's estimator (STE) by exploiting cross validation (CV). We propose leave-one-out cross-validation (LOOCV) choices for the shrinkage factors to optimize the beamforming performance, referred to as $\text{S}^2$CM-CV and STE-CV. The (weighted) out-of-sample output power of the beamfomer is chosen as a proxy of the beamformer performance and concise expressions of the LOOCV cost function are derived to allow fast optimization. For the large system regime, asymptotic approximations of the LOOCV cost functions are derived, yielding the $\text{S}^2$CM-AE and STE-AE. In general, the proposed algorithms are able to achieve near-oracle performance in choosing the linear shrinkage factors for MVDR beamforming. Simulation results are provided for validating the proposed methods.

Regularized Estimation of Kronecker-Structured Covariance Matrix

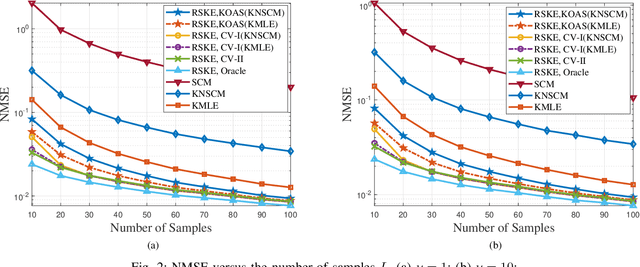
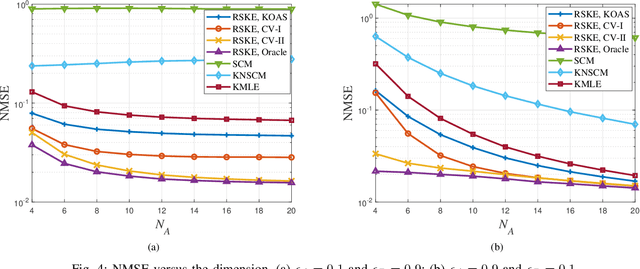
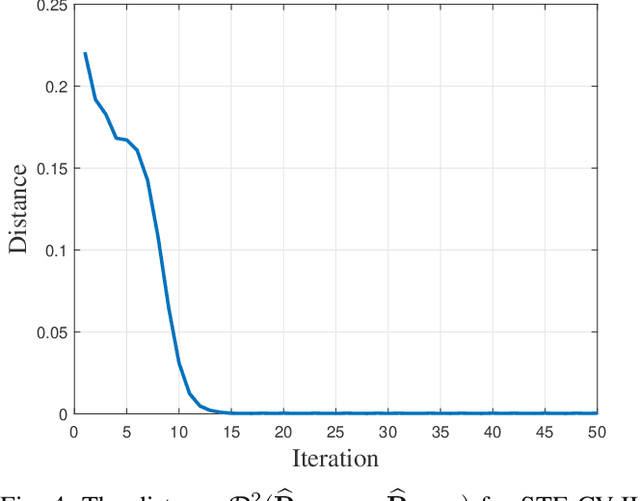
This paper investigates regularized estimation of Kronecker-structured covariance matrices (CM) for complex elliptically symmetric (CES) data. To obtain a well-conditioned estimate of the CM, we add penalty terms of Kullback-Leibler divergence to the negative log-likelihood function of the associated complex angular Gaussian (CAG) distribution. This is shown to be equivalent to regularizing Tyler's fixed-point equations by shrinkage. A sufficient condition that the solution exists is discussed. An iterative algorithm is applied to solve the resulting fixed-point iterations and its convergence is proved. In order to solve the critical problem of tuning the shrinkage factors, we then introduce three methods by exploiting oracle approximating shrinkage (OAS) and cross-validation (CV). When the training samples are limited, the proposed estimator, referred to as the robust shrinkage Kronecker estimator (RSKE), has better performance compared with several existing methods. Simulations are conducted for validating the proposed estimator and demonstrating its high performance.