Rational kernel-based interpolation for complex-valued frequency response functions

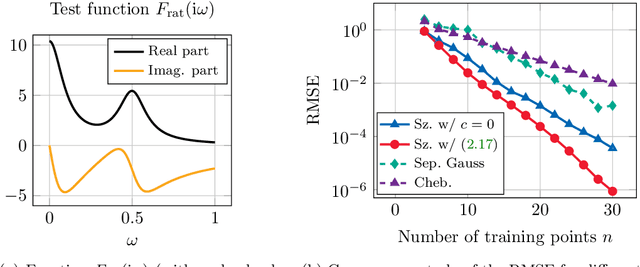
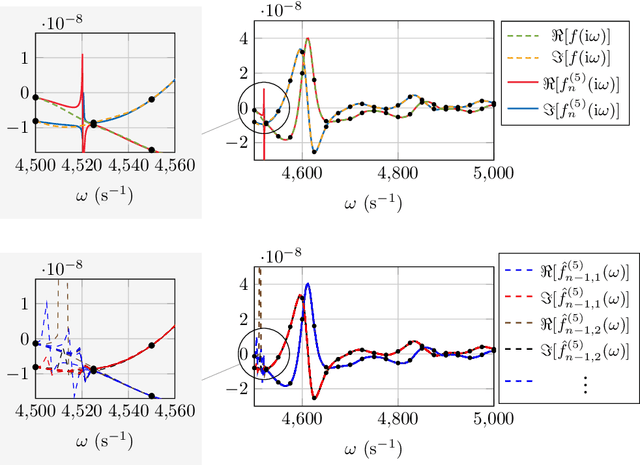
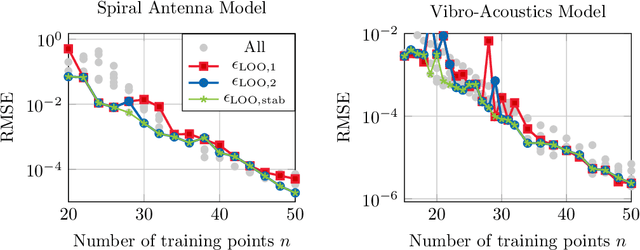
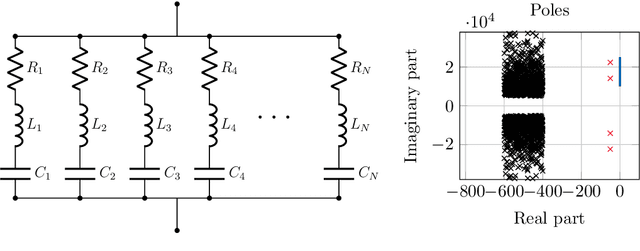
This work is concerned with the kernel-based approximation of a complex-valued function from data, where the frequency response function of a partial differential equation in the frequency domain is of particular interest. In this setting, kernel methods are employed more and more frequently, however, standard kernels do not perform well. Moreover, the role and mathematical implications of the underlying pair of kernels, which arises naturally in the complex-valued case, remain to be addressed. We introduce new reproducing kernel Hilbert spaces of complex-valued functions, and formulate the problem of complex-valued interpolation with a kernel pair as minimum norm interpolation in these spaces. Moreover, we combine the interpolant with a low-order rational function, where the order is adaptively selected based on a new model selection criterion. Numerical results on examples from different fields, including electromagnetics and acoustic examples, illustrate the performance of the method, also in comparison to available rational approximation methods.

Bayesian sequential design of computer experiments to estimate reliable sets

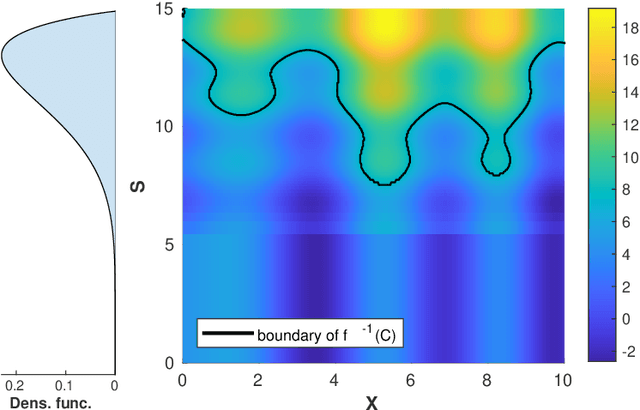
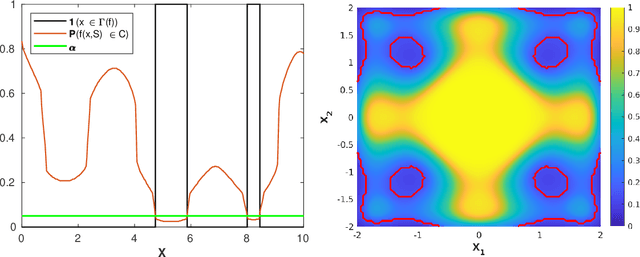
We consider an unknown multivariate function representing a system-such as a complex numerical simulator-taking both deterministic and uncertain inputs. Our objective is to estimate the set of deterministic inputs leading to outputs whose probability (with respect to the distribution of the uncertain inputs) to belong to a given set is controlled by a given threshold. To solve this problem, we propose a Bayesian strategy based on the Stepwise Uncertainty Reduction (SUR) principle to sequentially choose the points at which the function should be evaluated to approximate the set of interest. We illustrate its performance and interest in several numerical experiments.

Bayesian multi-objective optimization for stochastic simulators: an extension of the Pareto Active Learning method

This article focuses on the multi-objective optimization of stochastic simulators with high output variance, where the input space is finite and the objective functions are expensive to evaluate. We rely on Bayesian optimization algorithms, which use probabilistic models to make predictions about the functions to be optimized. The proposed approach is an extension of the Pareto Active Learning (PAL) algorithm for the estimation of Pareto-optimal solutions that makes it suitable for the stochastic setting. We named it Pareto Active Learning for Stochastic Simulators (PALS). The performance of PALS is assessed through numerical experiments over a set of bi-dimensional, bi-objective test problems. PALS exhibits superior performance when compared to other scalarization-based and random-search approaches.

Relaxed Gaussian process interpolation: a goal-oriented approach to Bayesian optimization

This work presents a new procedure for obtaining predictive distributions in the context of Gaussian process (GP) modeling, with a relaxation of the interpolation constraints outside some ranges of interest: the mean of the predictive distributions no longer necessarily interpolates the observed values when they are outside ranges of interest, but are simply constrained to remain outside. This method called relaxed Gaussian process (reGP) interpolation provides better predictive distributions in ranges of interest, especially in cases where a stationarity assumption for the GP model is not appropriate. It can be viewed as a goal-oriented method and becomes particularly interesting in Bayesian optimization, for example, for the minimization of an objective function, where good predictive distributions for low function values are important. When the expected improvement criterion and reGP are used for sequentially choosing evaluation points, the convergence of the resulting optimization algorithm is theoretically guaranteed (provided that the function to be optimized lies in the reproducing kernel Hilbert spaces attached to the known covariance of the underlying Gaussian process). Experiments indicate that using reGP instead of stationary GP models in Bayesian optimization is beneficial.

Gaussian process interpolation: the choice of the family of models is more important than that of the selection criterion

This article revisits the fundamental problem of parameter selection for Gaussian process interpolation. By choosing the mean and the covariance functions of a Gaussian process within parametric families, the user obtains a family of Bayesian procedures to perform predictions about the unknown function, and must choose a member of the family that will hopefully provide good predictive performances. We base our study on the general concept of scoring rules, which provides an effective framework for building leave-one-out selection and validation criteria, and a notion of extended likelihood criteria based on an idea proposed by Fasshauer and co-authors in 2009, which makes it possible to recover standard selection criteria such as, for instance, the generalized cross-validation criterion. Under this setting, we empirically show on several test problems of the literature that the choice of an appropriate family of models is often more important than the choice of a particular selection criterion (e.g., the likelihood versus a leave-one-out selection criterion). Moreover, our numerical results show that the regularity parameter of a Mat{\'e}rn covariance can be selected effectively by most selection criteria.

Numerical issues in maximum likelihood parameter estimation for Gaussian process regression

This article focuses on numerical issues in maximum likelihood parameter estimation for Gaussian process regression (GPR). This article investigates the origin of the numerical issues and provides simple but effective improvement strategies. This work targets a basic problem but a host of studies, particularly in the literature of Bayesian optimization, rely on off-the-shelf GPR implementations. For the conclusions of these studies to be reliable and reproducible, robust GPR implementations are critical.

Sequential design of multi-fidelity computer experiments: maximizing the rate of stepwise uncertainty reduction

This article deals with the sequential design of experiments for (deterministic or stochastic) multi-fidelity numerical simulators, that is, simulators that offer control over the accuracy of simulation of the physical phenomenon or system under study. Very often, accurate simulations correspond to high computational efforts whereas coarse simulations can be obtained at a smaller cost. In this setting, simulation results obtained at several levels of fidelity can be combined in order to estimate quantities of interest (the optimal value of the output, the probability that the output exceeds a given threshold...) in an efficient manner. To do so, we propose a new Bayesian sequential strategy called Maximal Rate of Stepwise Uncertainty Reduction (MR-SUR), that selects additional simulations to be performed by maximizing the ratio between the expected reduction of uncertainty and the cost of simulation. This generic strategy unifies several existing methods, and provides a principled approach to develop new ones. We assess its performance on several examples, including a computationally intensive problem of fire safety analysis where the quantity of interest is the probability of exceeding a tenability threshold during a building fire.

Towards new cross-validation-based estimators for Gaussian process regression: efficient adjoint computation of gradients

We consider the problem of estimating the parameters of the covariance function of a Gaussian process by cross-validation. We suggest using new cross-validation criteria derived from the literature of scoring rules. We also provide an efficient method for computing the gradient of a cross-validation criterion. To the best of our knowledge, our method is more efficient than what has been proposed in the literature so far. It makes it possible to lower the complexity of jointly evaluating leave-one-out criteria and their gradients.

A supermartingale approach to Gaussian process based sequential design of experiments

Gaussian process (GP) models have become a well-established frameworkfor the adaptive design of costly experiments, and notably of computerexperiments. GP-based sequential designs have been found practicallyefficient for various objectives, such as global optimization(estimating the global maximum or maximizer(s) of a function),reliability analysis (estimating a probability of failure) or theestimation of level sets and excursion sets. In this paper, we studythe consistency of an important class of sequential designs, known asstepwise uncertainty reduction (SUR) strategies. Our approach relieson the key observation that the sequence of residual uncertaintymeasures, in SUR strategies, is generally a supermartingale withrespect to the filtration generated by the observations. Thisobservation enables us to establish generic consistency results for abroad class of SUR strategies. The consistency of several popularsequential design strategies is then obtained by means of this generalresult. Notably, we establish the consistency of two SUR strategiesproposed by Bect, Ginsbourger, Li, Picheny and Vazquez (Stat. Comp.,2012)---to the best of our knowledge, these are the first proofs ofconsistency for GP-based sequential design algorithms dedicated to theestimation of excursion sets and their measure. We also establish anew, more general proof of consistency for the expected improvementalgorithm for global optimization which, unlike previous results inthe literature, applies to any GP with continuous sample paths.

Adaptive Design of Experiments for Conservative Estimation of Excursion Sets

We consider a Gaussian process model trained on few evaluations of an expensive-to-evaluate deterministic function and we study the problem of estimating a fixed excursion set of this function. We focus on conservative estimates as they allow control on false positives while minimizing false negatives. We introduce adaptive strategies that sequentially selects new evaluations of the function by reducing the uncertainty on conservative estimates. Following the Stepwise Uncertainty Reduction approach we obtain new evaluations by minimizing adapted criteria. We provide tractable formulae for the conservative criteria and we benchmark the method on random functions generated under the model assumptions in two and five dimensions. Finally the method is applied to a reliability engineering test case. Overall, the proposed strategy of minimizing false negatives in conservative estimation achieves competitive performance both in terms of model based and a-posteriori indicators.