Index-aware learning of circuits

Electrical circuits are present in a variety of technologies, making their design an important part of computer aided engineering. The growing number of tunable parameters that affect the final design leads to a need for new approaches of quantifying their impact. Machine learning may play a key role in this regard, however current approaches often make suboptimal use of existing knowledge about the system at hand. In terms of circuits, their description via modified nodal analysis is well-understood. This particular formulation leads to systems of differential-algebraic equations (DAEs) which bring with them a number of peculiarities, e.g. hidden constraints that the solution needs to fulfill. We aim to use the recently introduced dissection concept for DAEs that can decouple a given system into ordinary differential equations, only depending on differential variables, and purely algebraic equations that describe the relations between differential and algebraic variables. The idea then is to only learn the differential variables and reconstruct the algebraic ones using the relations from the decoupling. This approach guarantees that the algebraic constraints are fulfilled up to the accuracy of the nonlinear system solver, which represents the main benefit highlighted in this article.

Rational kernel-based interpolation for complex-valued frequency response functions

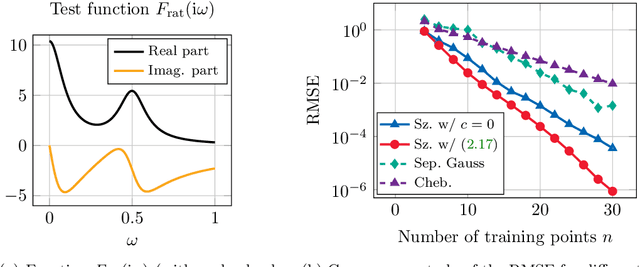
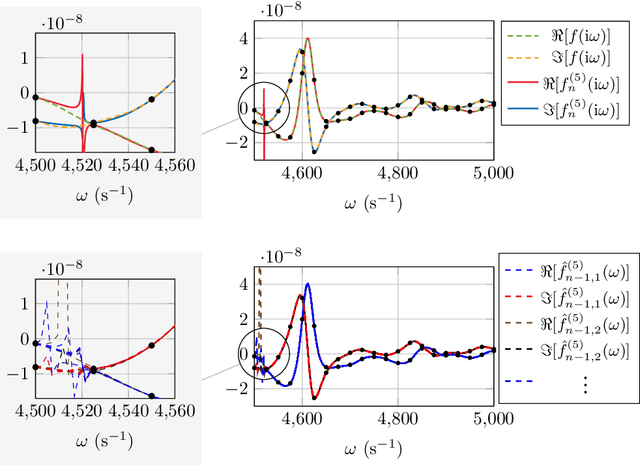
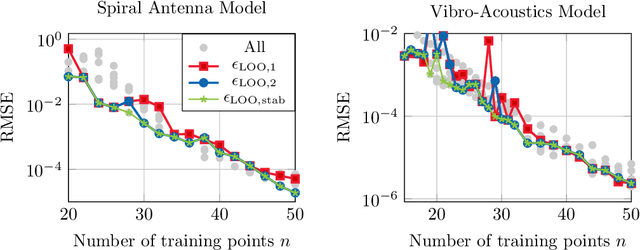
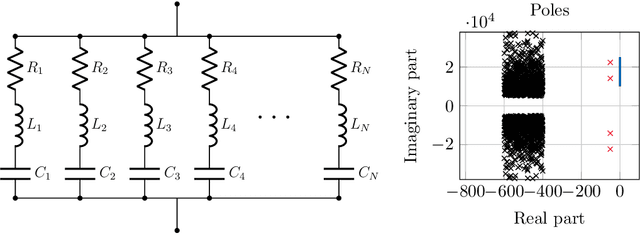
This work is concerned with the kernel-based approximation of a complex-valued function from data, where the frequency response function of a partial differential equation in the frequency domain is of particular interest. In this setting, kernel methods are employed more and more frequently, however, standard kernels do not perform well. Moreover, the role and mathematical implications of the underlying pair of kernels, which arises naturally in the complex-valued case, remain to be addressed. We introduce new reproducing kernel Hilbert spaces of complex-valued functions, and formulate the problem of complex-valued interpolation with a kernel pair as minimum norm interpolation in these spaces. Moreover, we combine the interpolant with a low-order rational function, where the order is adaptively selected based on a new model selection criterion. Numerical results on examples from different fields, including electromagnetics and acoustic examples, illustrate the performance of the method, also in comparison to available rational approximation methods.

Deep learning based Meta-modeling for Multi-objective Technology Optimization of Electrical Machines

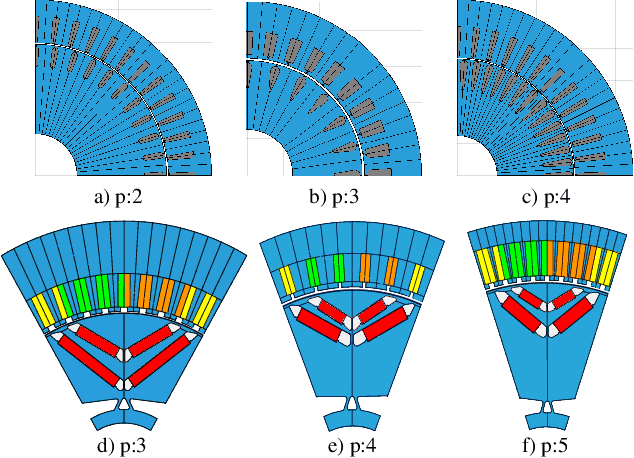
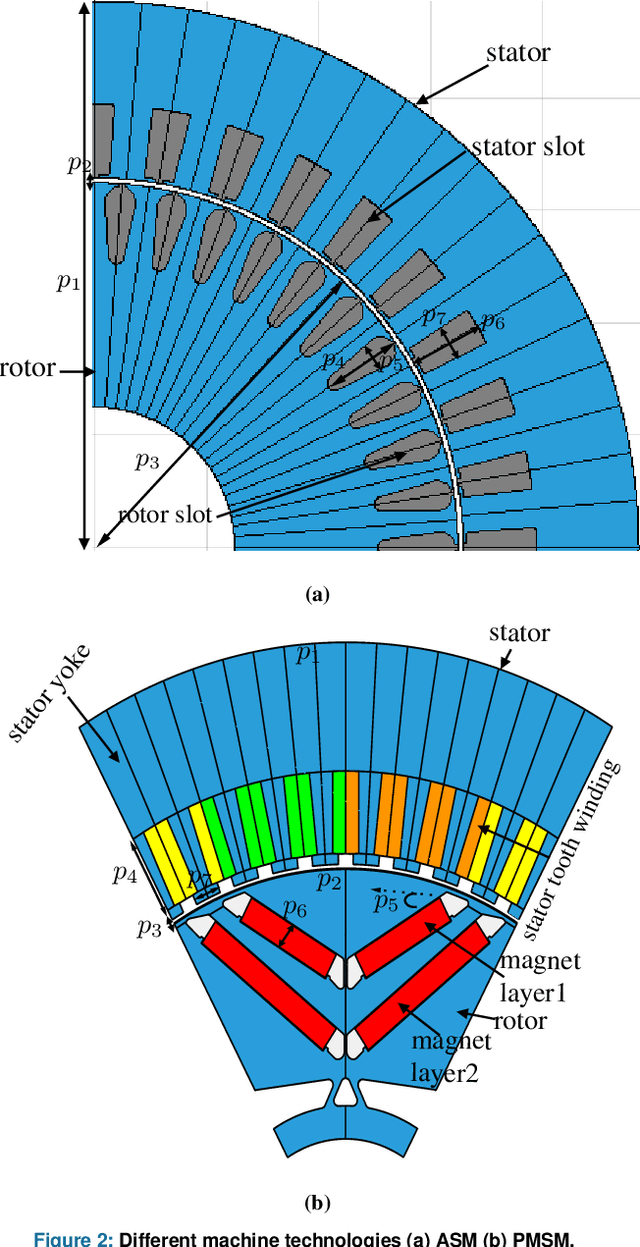
Optimization of rotating electrical machines is both time- and computationally expensive. Because of the different parametrization, design optimization is commonly executed separately for each machine technology. In this paper, we present the application of a variational auto-encoder (VAE) to optimize two different machine technologies simultaneously, namely an asynchronous machine and a permanent magnet synchronous machine. After training, we employ a deep neural network and a decoder as meta-models to predict global key performance indicators (KPIs) and generate associated new designs, respectively, through unified latent space in the optimization loop. Numerical results demonstrate concurrent parametric multi-objective technology optimization in the high-dimensional design space. The VAE-based approach is quantitatively compared to a classical deep learning-based direct approach for KPIs prediction.

Multi-Objective Optimization of Electrical Machines using a Hybrid Data-and Physics-Driven Approach

Magneto-static finite element (FE) simulations make numerical optimization of electrical machines very time-consuming and computationally intensive during the design stage. In this paper, we present the application of a hybrid data-and physics-driven model for numerical optimization of permanent magnet synchronous machines (PMSM). Following the data-driven supervised training, deep neural network (DNN) will act as a meta-model to characterize the electromagnetic behavior of PMSM by predicting intermediate FE measures. These intermediate measures are then post-processed with various physical models to compute the required key performance indicators (KPIs), e.g., torque, shaft power, and material costs. We perform multi-objective optimization with both classical FE and a hybrid approach using a nature-inspired evolutionary algorithm. We show quantitatively that the hybrid approach maintains the quality of Pareto results better or close to conventional FE simulation-based optimization while being computationally very cheap.

Performance analysis of Electrical Machines based on Electromagnetic System Characterization using Deep Learning

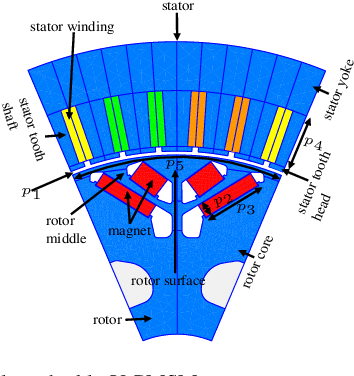
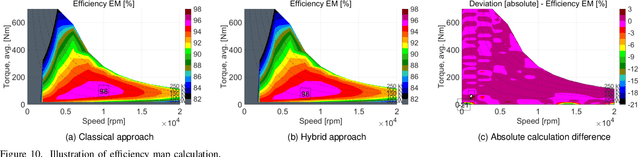
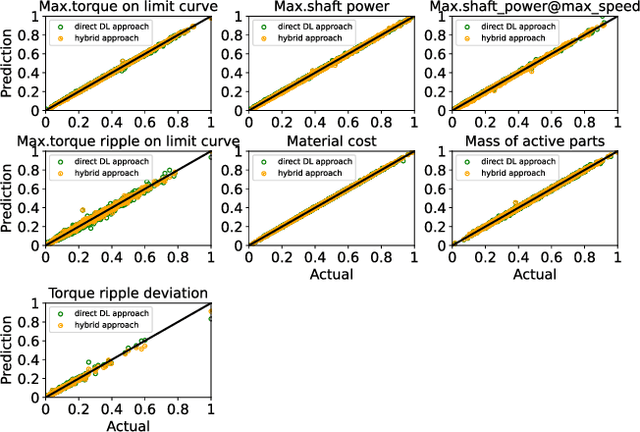
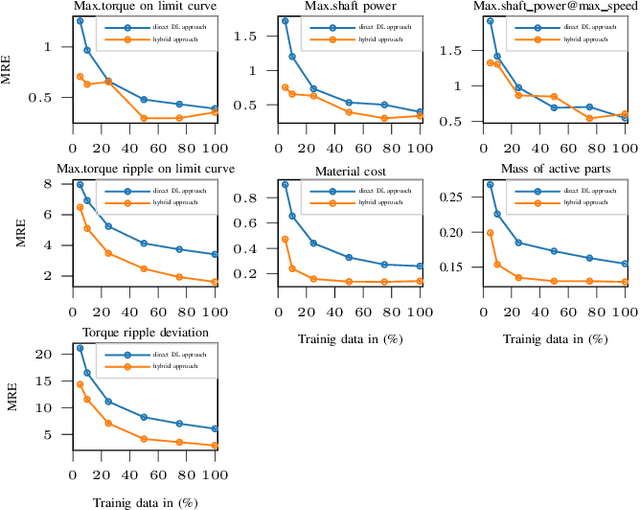
The numerical optimization of an electrical machine entails computationally intensive and time-consuming magneto-static finite element (FE) simulation. Generally, this FE-simulation involves varying input geometry, electrical, and material parameters of an electrical machine. The result of the FE simulation characterizes the electromagnetic behavior of the electrical machine. It usually includes nonlinear iron losses and electromagnetic torque and flux at different time-steps for an electrical cycle at each operating point (varying electrical input phase current and control angle). In this paper, we present a novel data-driven deep learning (DL) approach to approximate the electromagnetic behavior of an electrical machine by predicting intermediate measures that include non-linear iron losses, a non-negligible fraction ($\frac{1}{6}$ of a whole electrical period) of the electromagnetic torque and flux at different time-steps for each operating point. The remaining time-steps of the electromagnetic flux and torque for an electrical cycle are estimated by exploiting the magnetic state symmetry of the electrical machine. Then these calculations, along with the system parameters, are fed as input to the physics-based analytical models to estimate characteristic maps and key performance indicators (KPIs) such as material cost, maximum torque, power, torque ripple, etc. The key idea is to train the proposed multi-branch deep neural network (DNN) step by step on a large volume of stored FE data in a supervised manner. Preliminary results exhibit that the predictions of intermediate measures and the subsequent computations of KPIs are close to the ground truth for a new machine design in the input design space. In the end, the quantitative analysis validates that the hybrid approach is more accurate than the existing DNN-based direct prediction of KPIs, which avoids electromagnetic calculations.

Variational Autoencoder based Metamodeling for Multi-Objective Topology Optimization of Electrical Machines

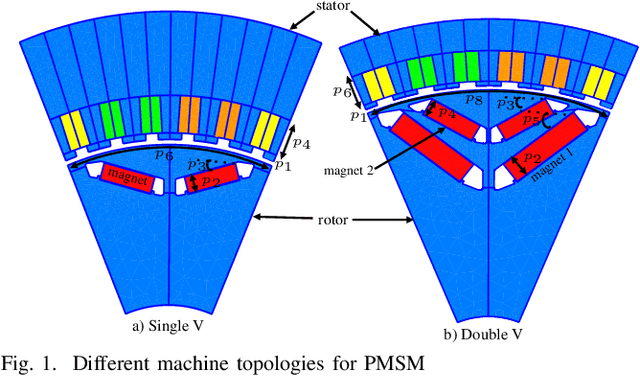
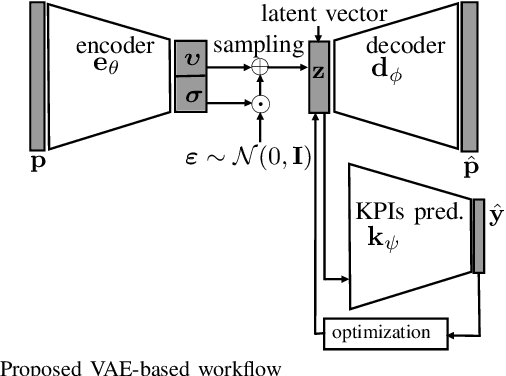
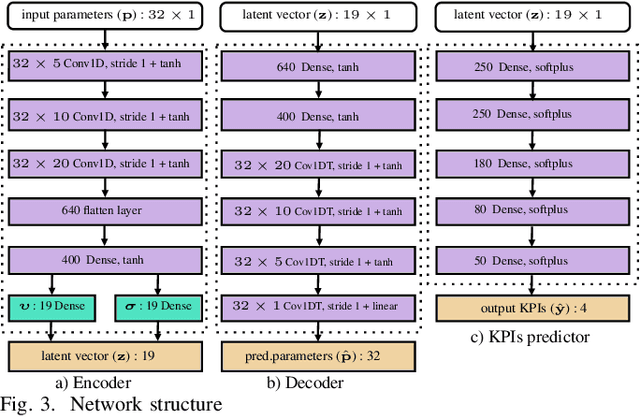
Conventional magneto-static finite element analysis of electrical machine models is time-consuming and computationally expensive. Since each machine topology has a distinct set of parameters, design optimization is commonly performed independently. This paper presents a novel method for predicting Key Performance Indicators (KPIs) of differently parameterized electrical machine topologies at the same time by mapping a high dimensional integrated design parameters in a lower dimensional latent space using a variational autoencoder. After training, via a latent space, the decoder and multi-layer neural network will function as meta-models for sampling new designs and predicting associated KPIs, respectively. This enables parameter-based concurrent multi-topology optimization.

Deep Learning-based Prediction of Key Performance Indicators for Electrical Machine

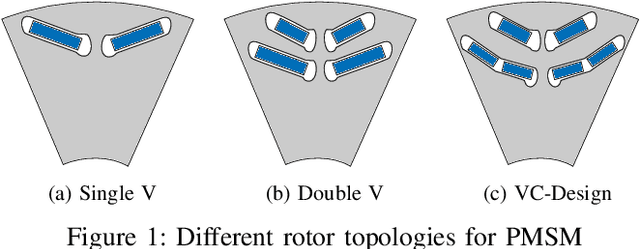
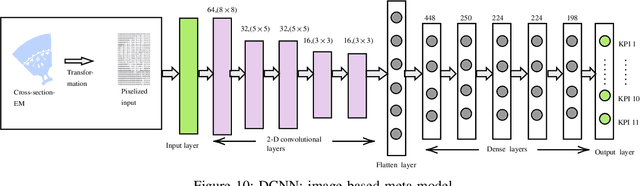
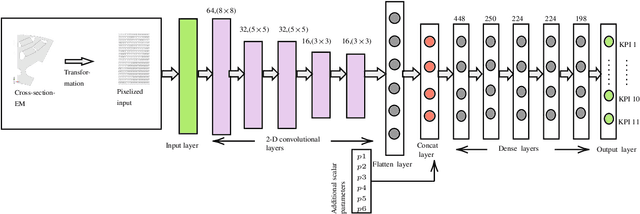
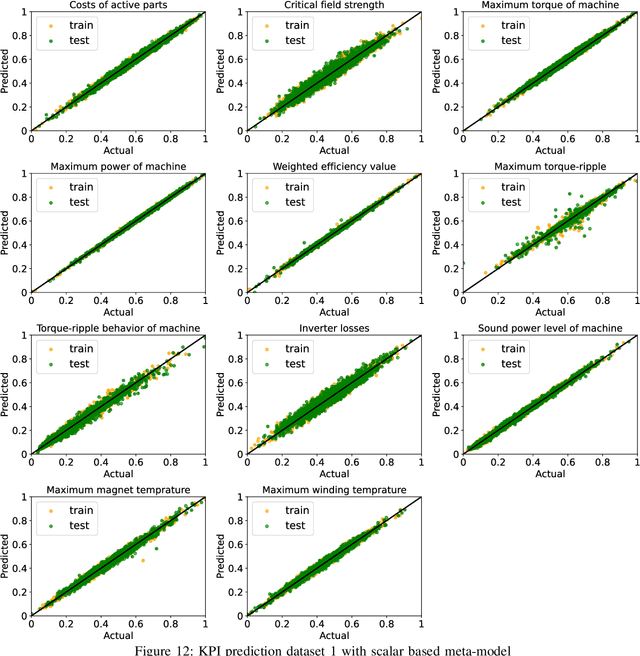
The design of an electrical machine can be quantified and evaluated by Key Performance Indicators (KPIs) such as maximum torque, critical field strength, costs of active parts, sound power, etc. Generally, cross-domain tool-chains are used to optimize all the KPIs from different domains (multi-objective optimization) by varying the given input parameters in the largest possible design space. This optimization process involves magneto-static finite element simulation to obtain these decisive KPIs. It makes the whole process a vehemently time-consuming computational task that counts on the availability of resources with the involvement of high computational cost. In this paper, a data-aided, deep learning-based meta-model is employed to predict the KPIs of an electrical machine quickly and with high accuracy to accelerate the full optimization process and reduce its computational costs. The focus is on analyzing various forms of input data that serve as a geometry representation of the machine. Namely, these are the cross-section image of the electrical machine that allows a very general description of the geometry relating to different topologies and the classical way with scalar parametrization of geometry. The impact of the resolution of the image is studied in detail. The results show a high prediction accuracy and proof that the validity of a deep learning-based meta-model to minimize the optimization time. The results also indicate that the prediction quality of an image-based approach can be made comparable to the classical way based on scalar parameters.

Yield Optimization using Hybrid Gaussian Process Regression and a Genetic Multi-Objective Approach

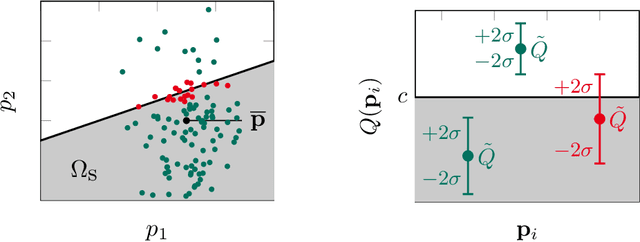
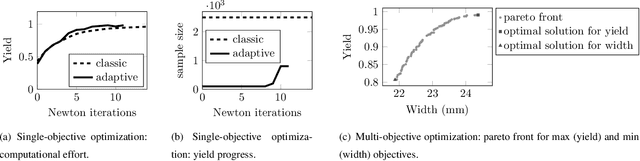
Quantification and minimization of uncertainty is an important task in the design of electromagnetic devices, which comes with high computational effort. We propose a hybrid approach combining the reliability and accuracy of a Monte Carlo analysis with the efficiency of a surrogate model based on Gaussian Process Regression. We present two optimization approaches. An adaptive Newton-MC to reduce the impact of uncertainty and a genetic multi-objective approach to optimize performance and robustness at the same time. For a dielectrical waveguide, used as a benchmark problem, the proposed methods outperform classic approaches.