Niklas Georg
Rational kernel-based interpolation for complex-valued frequency response functions
Jul 25, 2023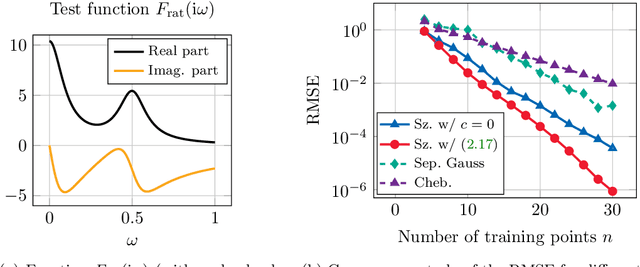
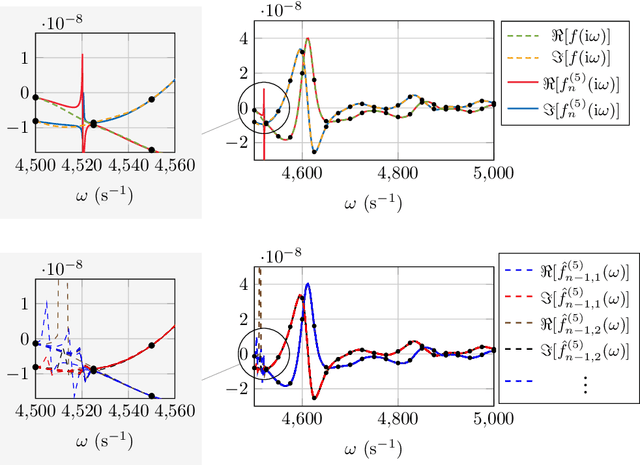
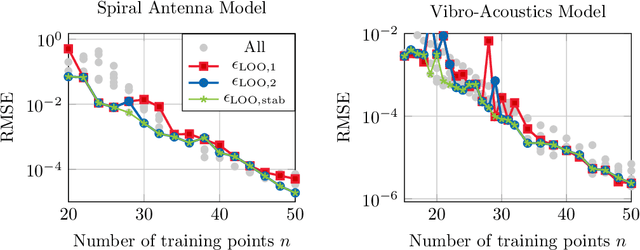
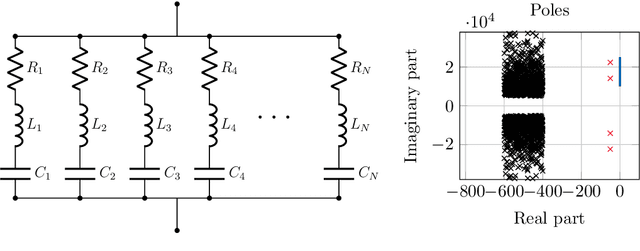
Abstract:This work is concerned with the kernel-based approximation of a complex-valued function from data, where the frequency response function of a partial differential equation in the frequency domain is of particular interest. In this setting, kernel methods are employed more and more frequently, however, standard kernels do not perform well. Moreover, the role and mathematical implications of the underlying pair of kernels, which arises naturally in the complex-valued case, remain to be addressed. We introduce new reproducing kernel Hilbert spaces of complex-valued functions, and formulate the problem of complex-valued interpolation with a kernel pair as minimum norm interpolation in these spaces. Moreover, we combine the interpolant with a low-order rational function, where the order is adaptively selected based on a new model selection criterion. Numerical results on examples from different fields, including electromagnetics and acoustic examples, illustrate the performance of the method, also in comparison to available rational approximation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge