Bayesian Active Learning of (small) Quantile Sets through Expected Estimator Modification

Given a multivariate function taking deterministic and uncertain inputs, we consider the problem of estimating a quantile set: a set of deterministic inputs for which the probability that the output belongs to a specific region remains below a given threshold. To solve this problem in the context of expensive-to-evaluate black-box functions, we propose a Bayesian active learning strategy based on Gaussian process modeling. The strategy is driven by a novel sampling criterion, which belongs to a broader principle that we refer to as Expected Estimator Modification (EEM). More specifically, the strategy relies on a novel sampling criterion combined with a sequential Monte Carlo framework that enables the construction of batch-sequential designs for the efficient estimation of small quantile sets. The performance of the strategy is illustrated on several synthetic examples and an industrial application case involving the ROTOR37 compressor model.

Gaussian process interpolation with conformal prediction: methods and comparative analysis

This article advocates the use of conformal prediction (CP) methods for Gaussian process (GP) interpolation to enhance the calibration of prediction intervals. We begin by illustrating that using a GP model with parameters selected by maximum likelihood often results in predictions that are not optimally calibrated. CP methods can adjust the prediction intervals, leading to better uncertainty quantification while maintaining the accuracy of the underlying GP model. We compare different CP variants and introduce a novel variant based on an asymmetric score. Our numerical experiments demonstrate the effectiveness of CP methods in improving calibration without compromising accuracy. This work aims to facilitate the adoption of CP methods in the GP community.

Bayesian sequential design of computer experiments to estimate reliable sets

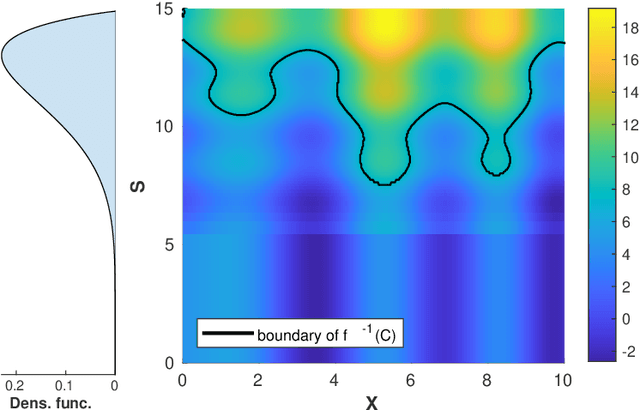
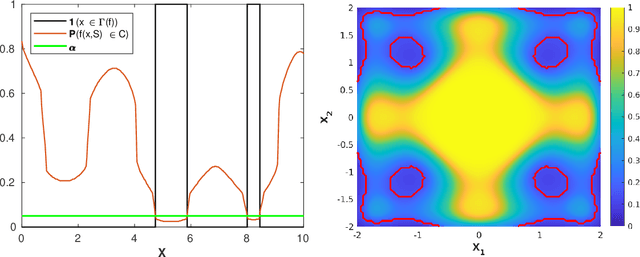
We consider an unknown multivariate function representing a system-such as a complex numerical simulator-taking both deterministic and uncertain inputs. Our objective is to estimate the set of deterministic inputs leading to outputs whose probability (with respect to the distribution of the uncertain inputs) to belong to a given set is controlled by a given threshold. To solve this problem, we propose a Bayesian strategy based on the Stepwise Uncertainty Reduction (SUR) principle to sequentially choose the points at which the function should be evaluated to approximate the set of interest. We illustrate its performance and interest in several numerical experiments.

Bayesian multi-objective optimization for stochastic simulators: an extension of the Pareto Active Learning method

This article focuses on the multi-objective optimization of stochastic simulators with high output variance, where the input space is finite and the objective functions are expensive to evaluate. We rely on Bayesian optimization algorithms, which use probabilistic models to make predictions about the functions to be optimized. The proposed approach is an extension of the Pareto Active Learning (PAL) algorithm for the estimation of Pareto-optimal solutions that makes it suitable for the stochastic setting. We named it Pareto Active Learning for Stochastic Simulators (PALS). The performance of PALS is assessed through numerical experiments over a set of bi-dimensional, bi-objective test problems. PALS exhibits superior performance when compared to other scalarization-based and random-search approaches.

Relaxed Gaussian process interpolation: a goal-oriented approach to Bayesian optimization

This work presents a new procedure for obtaining predictive distributions in the context of Gaussian process (GP) modeling, with a relaxation of the interpolation constraints outside some ranges of interest: the mean of the predictive distributions no longer necessarily interpolates the observed values when they are outside ranges of interest, but are simply constrained to remain outside. This method called relaxed Gaussian process (reGP) interpolation provides better predictive distributions in ranges of interest, especially in cases where a stationarity assumption for the GP model is not appropriate. It can be viewed as a goal-oriented method and becomes particularly interesting in Bayesian optimization, for example, for the minimization of an objective function, where good predictive distributions for low function values are important. When the expected improvement criterion and reGP are used for sequentially choosing evaluation points, the convergence of the resulting optimization algorithm is theoretically guaranteed (provided that the function to be optimized lies in the reproducing kernel Hilbert spaces attached to the known covariance of the underlying Gaussian process). Experiments indicate that using reGP instead of stationary GP models in Bayesian optimization is beneficial.

Gaussian process interpolation: the choice of the family of models is more important than that of the selection criterion

This article revisits the fundamental problem of parameter selection for Gaussian process interpolation. By choosing the mean and the covariance functions of a Gaussian process within parametric families, the user obtains a family of Bayesian procedures to perform predictions about the unknown function, and must choose a member of the family that will hopefully provide good predictive performances. We base our study on the general concept of scoring rules, which provides an effective framework for building leave-one-out selection and validation criteria, and a notion of extended likelihood criteria based on an idea proposed by Fasshauer and co-authors in 2009, which makes it possible to recover standard selection criteria such as, for instance, the generalized cross-validation criterion. Under this setting, we empirically show on several test problems of the literature that the choice of an appropriate family of models is often more important than the choice of a particular selection criterion (e.g., the likelihood versus a leave-one-out selection criterion). Moreover, our numerical results show that the regularity parameter of a Mat{\'e}rn covariance can be selected effectively by most selection criteria.

Numerical issues in maximum likelihood parameter estimation for Gaussian process regression

This article focuses on numerical issues in maximum likelihood parameter estimation for Gaussian process regression (GPR). This article investigates the origin of the numerical issues and provides simple but effective improvement strategies. This work targets a basic problem but a host of studies, particularly in the literature of Bayesian optimization, rely on off-the-shelf GPR implementations. For the conclusions of these studies to be reliable and reproducible, robust GPR implementations are critical.

Sequential design of multi-fidelity computer experiments: maximizing the rate of stepwise uncertainty reduction

This article deals with the sequential design of experiments for (deterministic or stochastic) multi-fidelity numerical simulators, that is, simulators that offer control over the accuracy of simulation of the physical phenomenon or system under study. Very often, accurate simulations correspond to high computational efforts whereas coarse simulations can be obtained at a smaller cost. In this setting, simulation results obtained at several levels of fidelity can be combined in order to estimate quantities of interest (the optimal value of the output, the probability that the output exceeds a given threshold...) in an efficient manner. To do so, we propose a new Bayesian sequential strategy called Maximal Rate of Stepwise Uncertainty Reduction (MR-SUR), that selects additional simulations to be performed by maximizing the ratio between the expected reduction of uncertainty and the cost of simulation. This generic strategy unifies several existing methods, and provides a principled approach to develop new ones. We assess its performance on several examples, including a computationally intensive problem of fire safety analysis where the quantity of interest is the probability of exceeding a tenability threshold during a building fire.

Towards new cross-validation-based estimators for Gaussian process regression: efficient adjoint computation of gradients

We consider the problem of estimating the parameters of the covariance function of a Gaussian process by cross-validation. We suggest using new cross-validation criteria derived from the literature of scoring rules. We also provide an efficient method for computing the gradient of a cross-validation criterion. To the best of our knowledge, our method is more efficient than what has been proposed in the literature so far. It makes it possible to lower the complexity of jointly evaluating leave-one-out criteria and their gradients.

Sequential design of experiments to estimate a probability of exceeding a threshold in a multi-fidelity stochastic simulator

In this article, we consider a stochastic numerical simulator to assess the impact of some factors on a phenomenon. The simulator is seen as a black box with inputs and outputs. The quality of a simulation, hereafter referred to as fidelity, is assumed to be tunable by means of an additional input of the simulator (e.g., a mesh size parameter): high-fidelity simulations provide more accurate results, but are time-consuming. Using a limited computation-time budget, we want to estimate, for any value of the physical inputs, the probability that a certain scalar output of the simulator will exceed a given critical threshold at the highest fidelity level. The problem is addressed in a Bayesian framework, using a Gaussian process model of the multi-fidelity simulator. We consider a Bayesian estimator of the probability, together with an associated measure of uncertainty, and propose a new multi-fidelity sequential design strategy, called Maximum Speed of Uncertainty Reduction (MSUR), to select the value of physical inputs and the fidelity level of new simulations. The MSUR strategy is tested on an example.