Gaussian process interpolation: the choice of the family of models is more important than that of the selection criterion

This article revisits the fundamental problem of parameter selection for Gaussian process interpolation. By choosing the mean and the covariance functions of a Gaussian process within parametric families, the user obtains a family of Bayesian procedures to perform predictions about the unknown function, and must choose a member of the family that will hopefully provide good predictive performances. We base our study on the general concept of scoring rules, which provides an effective framework for building leave-one-out selection and validation criteria, and a notion of extended likelihood criteria based on an idea proposed by Fasshauer and co-authors in 2009, which makes it possible to recover standard selection criteria such as, for instance, the generalized cross-validation criterion. Under this setting, we empirically show on several test problems of the literature that the choice of an appropriate family of models is often more important than the choice of a particular selection criterion (e.g., the likelihood versus a leave-one-out selection criterion). Moreover, our numerical results show that the regularity parameter of a Mat{\'e}rn covariance can be selected effectively by most selection criteria.

Towards new cross-validation-based estimators for Gaussian process regression: efficient adjoint computation of gradients

We consider the problem of estimating the parameters of the covariance function of a Gaussian process by cross-validation. We suggest using new cross-validation criteria derived from the literature of scoring rules. We also provide an efficient method for computing the gradient of a cross-validation criterion. To the best of our knowledge, our method is more efficient than what has been proposed in the literature so far. It makes it possible to lower the complexity of jointly evaluating leave-one-out criteria and their gradients.

A Bayesian approach to constrained single- and multi-objective optimization

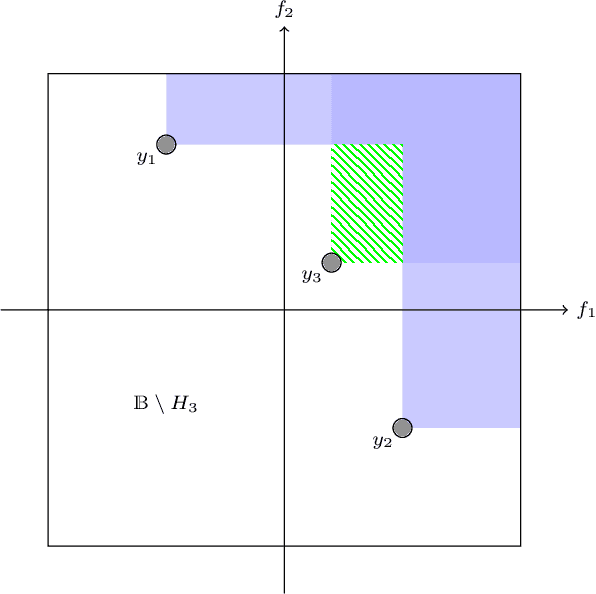
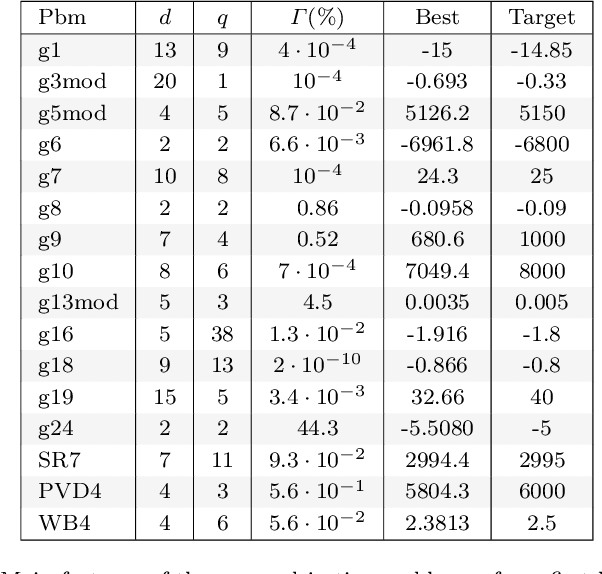
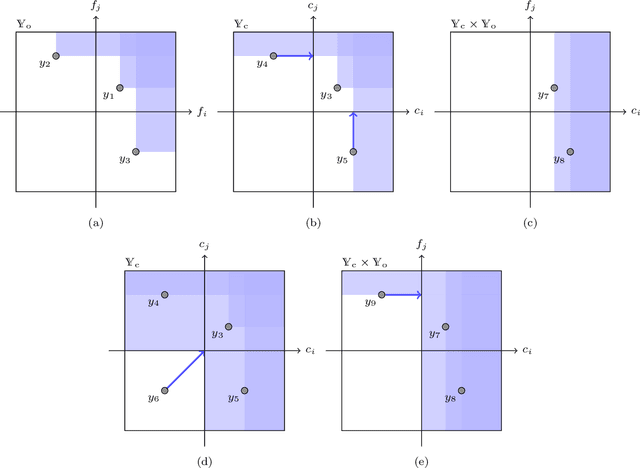
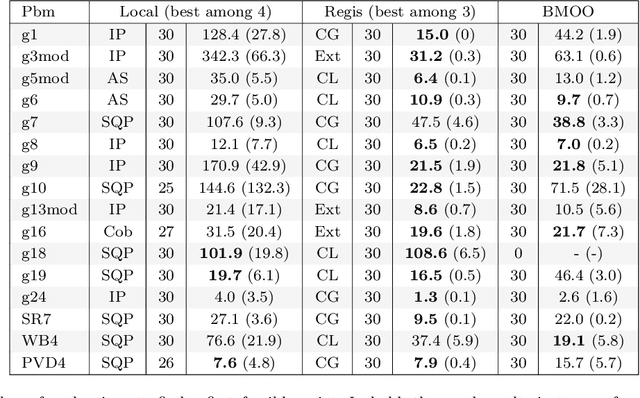
This article addresses the problem of derivative-free (single- or multi-objective) optimization subject to multiple inequality constraints. Both the objective and constraint functions are assumed to be smooth, non-linear and expensive to evaluate. As a consequence, the number of evaluations that can be used to carry out the optimization is very limited, as in complex industrial design optimization problems. The method we propose to overcome this difficulty has its roots in both the Bayesian and the multi-objective optimization literatures. More specifically, an extended domination rule is used to handle objectives and constraints in a unified way, and a corresponding expected hyper-volume improvement sampling criterion is proposed. This new criterion is naturally adapted to the search of a feasible point when none is available, and reduces to existing Bayesian sampling criteria---the classical Expected Improvement (EI) criterion and some of its constrained/multi-objective extensions---as soon as at least one feasible point is available. The calculation and optimization of the criterion are performed using Sequential Monte Carlo techniques. In particular, an algorithm similar to the subset simulation method, which is well known in the field of structural reliability, is used to estimate the criterion. The method, which we call BMOO (for Bayesian Multi-Objective Optimization), is compared to state-of-the-art algorithms for single- and multi-objective constrained optimization.