Generating Rationales in Visual Question Answering

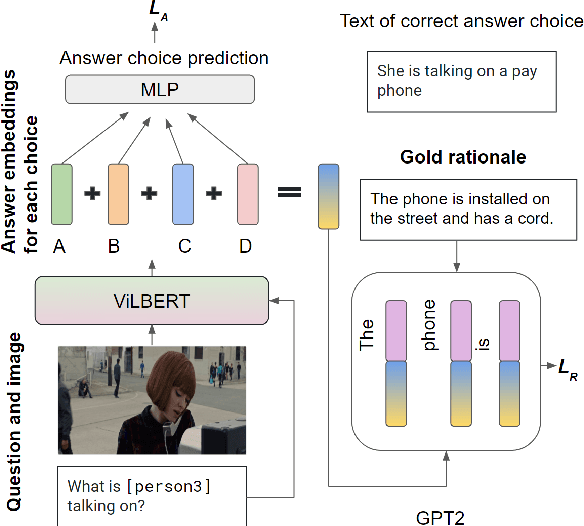
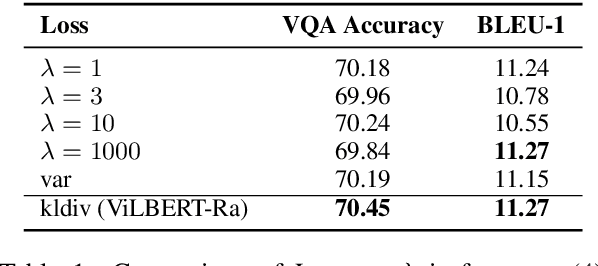
Despite recent advances in Visual QuestionAnswering (VQA), it remains a challenge todetermine how much success can be attributedto sound reasoning and comprehension ability.We seek to investigate this question by propos-ing a new task ofrationale generation. Es-sentially, we task a VQA model with generat-ing rationales for the answers it predicts. Weuse data from the Visual Commonsense Rea-soning (VCR) task, as it contains ground-truthrationales along with visual questions and an-swers. We first investigate commonsense un-derstanding in one of the leading VCR mod-els, ViLBERT, by generating rationales frompretrained weights using a state-of-the-art lan-guage model, GPT-2. Next, we seek to jointlytrain ViLBERT with GPT-2 in an end-to-endfashion with the dual task of predicting the an-swer in VQA and generating rationales. Weshow that this kind of training injects com-monsense understanding in the VQA modelthrough quantitative and qualitative evaluationmetrics

Faster Algorithms for Max-Product Message-Passing

Maximum A Posteriori inference in graphical models is often solved via message-passing algorithms, such as the junction-tree algorithm, or loopy belief-propagation. The exact solution to this problem is well known to be exponential in the size of the model's maximal cliques after it is triangulated, while approximate inference is typically exponential in the size of the model's factors. In this paper, we take advantage of the fact that many models have maximal cliques that are larger than their constituent factors, and also of the fact that many factors consist entirely of latent variables (i.e., they do not depend on an observation). This is a common case in a wide variety of applications, including grids, trees, and ring-structured models. In such cases, we are able to decrease the exponent of complexity for message-passing by 0.5 for both exact and approximate inference.

Robust Near-Isometric Matching via Structured Learning of Graphical Models

Models for near-rigid shape matching are typically based on distance-related features, in order to infer matches that are consistent with the isometric assumption. However, real shapes from image datasets, even when expected to be related by "almost isometric" transformations, are actually subject not only to noise but also, to some limited degree, to variations in appearance and scale. In this paper, we introduce a graphical model that parameterises appearance, distance, and angle features and we learn all of the involved parameters via structured prediction. The outcome is a model for near-rigid shape matching which is robust in the sense that it is able to capture the possibly limited but still important scale and appearance variations. Our experimental results reveal substantial improvements upon recent successful models, while maintaining similar running times.

Learning Graph Matching

As a fundamental problem in pattern recognition, graph matching has applications in a variety of fields, from computer vision to computational biology. In graph matching, patterns are modeled as graphs and pattern recognition amounts to finding a correspondence between the nodes of different graphs. Many formulations of this problem can be cast in general as a quadratic assignment problem, where a linear term in the objective function encodes node compatibility and a quadratic term encodes edge compatibility. The main research focus in this theme is about designing efficient algorithms for approximately solving the quadratic assignment problem, since it is NP-hard. In this paper we turn our attention to a different question: how to estimate compatibility functions such that the solution of the resulting graph matching problem best matches the expected solution that a human would manually provide. We present a method for learning graph matching: the training examples are pairs of graphs and the `labels' are matches between them. Our experimental results reveal that learning can substantially improve the performance of standard graph matching algorithms. In particular, we find that simple linear assignment with such a learning scheme outperforms Graduated Assignment with bistochastic normalisation, a state-of-the-art quadratic assignment relaxation algorithm.

Graph rigidity, Cyclic Belief Propagation and Point Pattern Matching

A recent paper \cite{CaeCaeSchBar06} proposed a provably optimal, polynomial time method for performing near-isometric point pattern matching by means of exact probabilistic inference in a chordal graphical model. Their fundamental result is that the chordal graph in question is shown to be globally rigid, implying that exact inference provides the same matching solution as exact inference in a complete graphical model. This implies that the algorithm is optimal when there is no noise in the point patterns. In this paper, we present a new graph which is also globally rigid but has an advantage over the graph proposed in \cite{CaeCaeSchBar06}: its maximal clique size is smaller, rendering inference significantly more efficient. However, our graph is not chordal and thus standard Junction Tree algorithms cannot be directly applied. Nevertheless, we show that loopy belief propagation in such a graph converges to the optimal solution. This allows us to retain the optimality guarantee in the noiseless case, while substantially reducing both memory requirements and processing time. Our experimental results show that the accuracy of the proposed solution is indistinguishable from that of \cite{CaeCaeSchBar06} when there is noise in the point patterns.