Making Bayesian Predictive Models Interpretable: A Decision Theoretic Approach

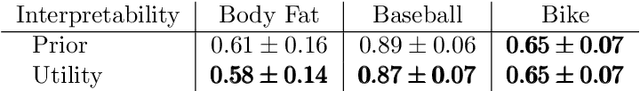
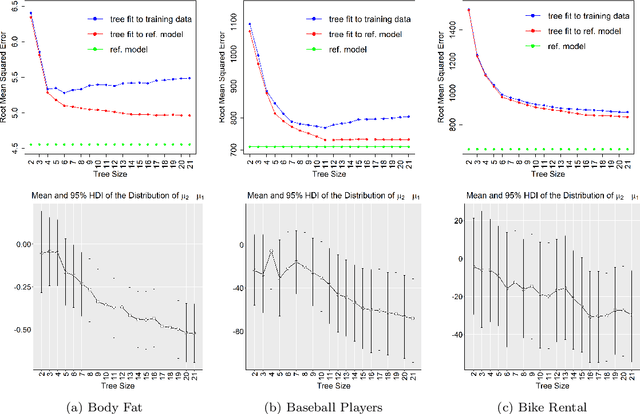
A salient approach to interpretable machine learning is to restrict modeling to simple and hence understandable models. In the Bayesian framework, this can be pursued by restricting the model structure and prior to favor interpretable models. Fundamentally, however, interpretability is about users' preferences, not the data generation mechanism: it is more natural to formulate interpretability as a utility function. In this work, we propose an interpretability utility, which explicates the trade-off between explanation fidelity and interpretability in the Bayesian framework. The method consists of two steps. First, a reference model, possibly a black-box Bayesian predictive model compromising no accuracy, is constructed and fitted to the training data. Second, a proxy model from an interpretable model family that best mimics the predictive behaviour of the reference model is found by optimizing the interpretability utility function. The approach is model agnostic - neither the interpretable model nor the reference model are restricted to be from a certain class of models - and the optimization problem can be solved using standard tools in the chosen model family. Through experiments on real-word data sets using decision trees as interpretable models and Bayesian additive regression models as reference models, we show that for the same level of interpretability, our approach generates more accurate models than the earlier alternative of restricting the prior. We also propose a systematic way to measure stabilities of interpretabile models constructed by different interpretability approaches and show that our proposed approach generates more stable models.

Pushing the Limits of Importance Sampling through Iterative Moment Matching

The accuracy of an integral approximation via Monte Carlo sampling depends on the distribution of the integrand and the existence of its moments. In importance sampling, the choice of the proposal distribution markedly affects the existence of these moments and thus the accuracy of the obtained integral approximation. In this work, we present a method for improving the proposal distribution that applies to complicated distributions which are not available in closed form. The method iteratively matches the moments of a sample from the proposal distribution to their importance weighted moments, and is applicable to both standard importance sampling and self-normalized importance sampling. We apply the method to Bayesian leave-one-out cross-validation and show that it can significantly improve the accuracy of model assessment compared to regular Monte Carlo sampling or importance sampling when there are influential observations. We also propose a diagnostic method that can estimate the convergence rate of any Monte Carlo estimator from a finite random sample.

Variable selection for Gaussian processes via sensitivity analysis of the posterior predictive distribution

Variable selection for Gaussian process models is often done using automatic relevance determination, which uses the inverse length-scale parameter of each input variable as a proxy for variable relevance. This implicitly determined relevance has several drawbacks that prevent the selection of optimal input variables in terms of predictive performance. To improve on this, we propose two novel variable selection methods for Gaussian process models that utilize the predictions of a full model in the vicinity of the training points and thereby rank the variables based on their predictive relevance. Our empirical results on synthetic and real world data sets demonstrate improved variable selection compared to automatic relevance determination in terms of variability and predictive performance.

Comparison of Bayesian predictive methods for model selection

The goal of this paper is to compare several widely used Bayesian model selection methods in practical model selection problems, highlight their differences and give recommendations about the preferred approaches. We focus on the variable subset selection for regression and classification and perform several numerical experiments using both simulated and real world data. The results show that the optimization of a utility estimate such as the cross-validation (CV) score is liable to finding overfitted models due to relatively high variance in the utility estimates when the data is scarce. This can also lead to substantial selection induced bias and optimism in the performance evaluation for the selected model. From a predictive viewpoint, best results are obtained by accounting for model uncertainty by forming the full encompassing model, such as the Bayesian model averaging solution over the candidate models. If the encompassing model is too complex, it can be robustly simplified by the projection method, in which the information of the full model is projected onto the submodels. This approach is substantially less prone to overfitting than selection based on CV-score. Overall, the projection method appears to outperform also the maximum a posteriori model and the selection of the most probable variables. The study also demonstrates that the model selection can greatly benefit from using cross-validation outside the searching process both for guiding the model size selection and assessing the predictive performance of the finally selected model.