Data-Efficient Meningioma Segmentation via Implicit Spatiotemporal Mixing and Sim2Real Semantic Injection

The performance of medical image segmentation is increasingly defined by the efficiency of data utilization rather than merely the volume of raw data. Accurate segmentation, particularly for complex pathologies like meningiomas, demands that models fully exploit the latent information within limited high-quality annotations. To maximize the value of existing datasets, we propose a novel dual-augmentation framework that synergistically integrates spatial manifold expansion and semantic object injection. Specifically, we leverage Implicit Neural Representations (INR) to model continuous velocity fields. Unlike previous methods, we perform linear mixing on the integrated deformation fields, enabling the efficient generation of anatomically plausible variations by interpolating within the deformation space. This approach allows for the extensive exploration of structural diversity from a small set of anchors. Furthermore, we introduce a Sim2Real lesion injection module. This module constructs a high-fidelity simulation domain by transplanting lesion textures into healthy anatomical backgrounds, effectively bridging the gap between synthetic augmentation and real-world pathology. Comprehensive experiments on a hybrid dataset demonstrate that our framework significantly enhances the data efficiency and robustness of state-of-the-art models, including nnU-Net and U-Mamba, offering a potent strategy for high-performance medical image analysis with limited annotation budgets.

Data-driven Optimal Power Flow: A Physics-Informed Machine Learning Approach

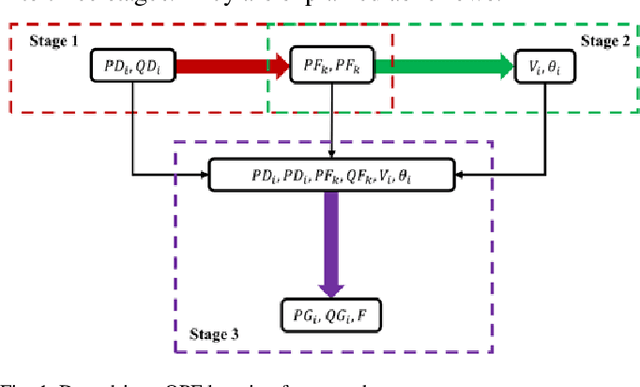
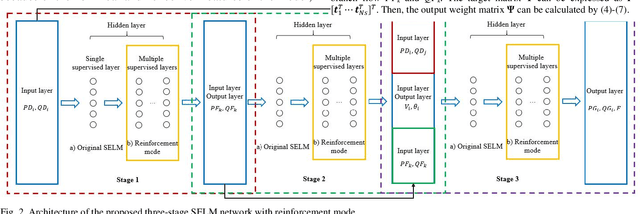
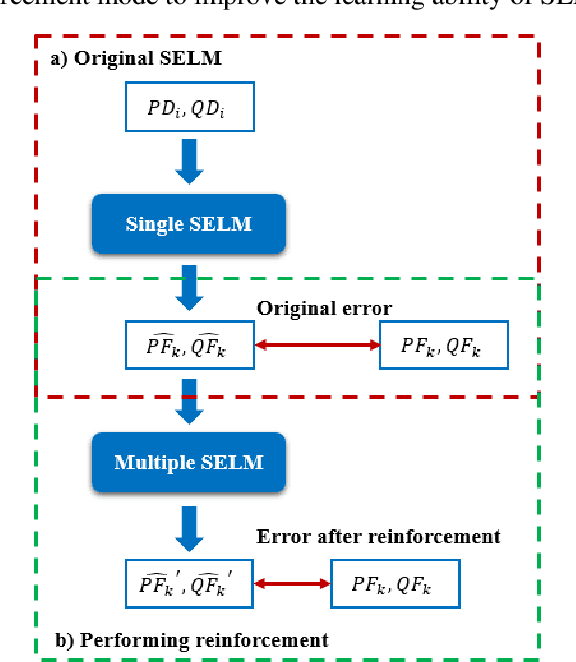
This paper proposes a data-driven approach for optimal power flow (OPF) based on the stacked extreme learning machine (SELM) framework. SELM has a fast training speed and does not require the time-consuming parameter tuning process compared with the deep learning algorithms. However, the direct application of SELM for OPF is not tractable due to the complicated relationship between the system operating status and the OPF solutions. To this end, a data-driven OPF regression framework is developed that decomposes the OPF model features into three stages. This not only reduces the learning complexity but also helps correct the learning bias. A sample pre-classification strategy based on active constraint identification is also developed to achieve enhanced feature attractions. Numerical results carried out on IEEE and Polish benchmark systems demonstrate that the proposed method outperforms other alternatives. It is also shown that the proposed method can be easily extended to address different test systems by adjusting only a few hyperparameters.

Fast Calculation of Probabilistic Optimal Power Flow: A Deep Learning Approach

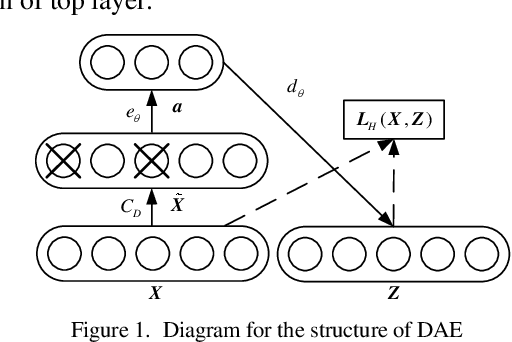
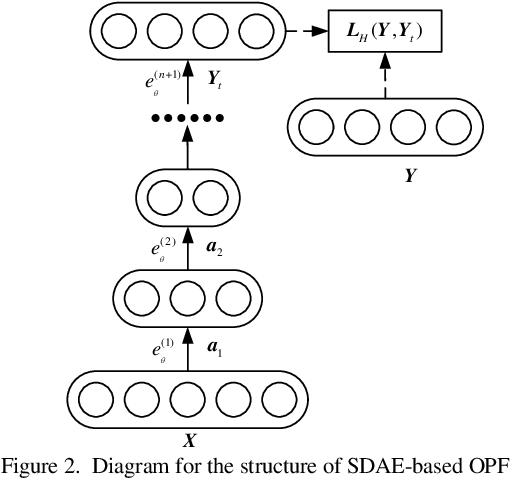
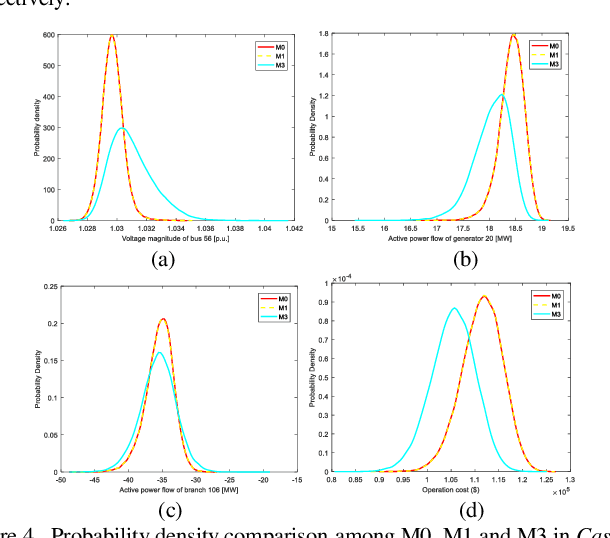
Probabilistic optimal power flow (POPF) is an important analytical tool to ensure the secure and economic operation of power systems. POPF needs to solve enormous nonlinear and nonconvex optimization problems. The huge computational burden has become the major bottleneck for the practical application. This paper presents a deep learning approach to solve the POPF problem efficiently and accurately. Taking advantage of the deep structure and reconstructive strategy of stacked denoising auto encoders (SDAE), a SDAE-based optimal power flow (OPF) is developed to extract the high-level nonlinear correlations between the system operating condition and the OPF solution. A training process is designed to learn the feature of POPF. The trained SDAE network can be utilized to conveniently calculate the OPF solution of random samples generated by Monte-Carlo simulation (MCS) without the need of optimization. A modified IEEE 118-bus power system is simulated to demonstrate the effectiveness of the proposed method.

Fast Calculation of Probabilistic Power Flow: A Model-based Deep Learning Approach

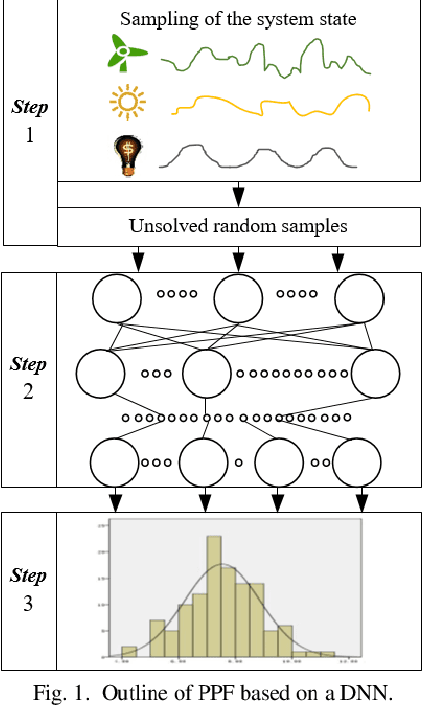
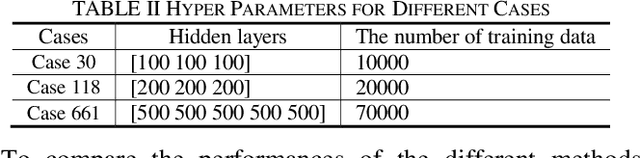
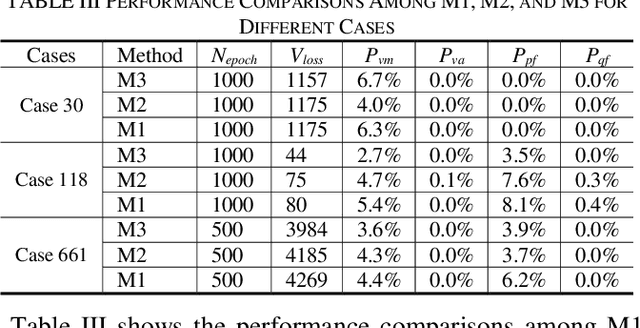
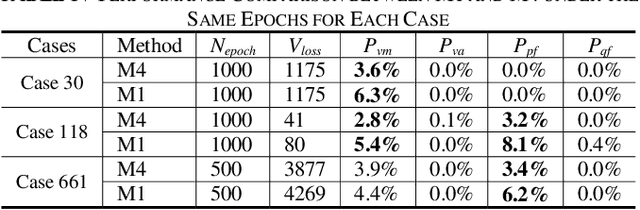
Probabilistic power flow (PPF) plays a critical role in the analysis of power systems. However, its high computational burden makes practical implementations challenging. This paper proposes a model-based deep learning approach to overcome these computational challenges. A deep neural network (DNN) is used to approximate the power flow calculation process, and is trained according to the physical power flow equations to improve its learning ability. The training process consists of several steps: 1) the branch flows are added into the objective function of the DNN as a penalty term, which improves the generalization ability of the DNN; 2) the gradients used in back propagation are simplified according to the physical characteristics of the transmission grid, which accelerates the training speed while maintaining effective guidance of the physical model; and 3) an improved initialization method for the DNN parameters is proposed to improve the convergence speed. The simulation results demonstrate the accuracy and efficiency of the proposed method in standard IEEE and utility benchmark systems.