Predicting Requests in Large-Scale Online P2P Ridesharing

Peer-to-peer ridesharing (P2P-RS) enables people to arrange one-time rides with their own private cars, without the involvement of professional drivers. It is a prominent collective intelligence application producing significant benefits both for individuals (reduced costs) and for the entire community (reduced pollution and traffic), as we showed in a recent publication where we proposed an online approximate solution algorithm for large-scale P2P-RS. In this paper we tackle the fundamental question of assessing the benefit of predicting ridesharing requests in the context of P2P-RS optimisation. Results on a public real-world show that, by employing a perfect predictor, the total reward can be improved by 5.27% with a forecast horizon of 1 minute. On the other hand, a vanilla long short-term memory neural network cannot improve upon a baseline predictor that simply replicates the previous day's requests, whilst achieving an almost-double accuracy.

TAIP: an anytime algorithm for allocating student teams to internship programs

In scenarios that require teamwork, we usually have at hand a variety of specific tasks, for which we need to form a team in order to carry out each one. Here we target the problem of matching teams with tasks within the context of education, and specifically in the context of forming teams of students and allocating them to internship programs. First we provide a formalization of the Team Allocation for Internship Programs Problem, and show the computational hardness of solving it optimally. Thereafter, we propose TAIP, a heuristic algorithm that generates an initial team allocation which later on attempts to improve in an iterative process. Moreover, we conduct a systematic evaluation to show that TAIP reaches optimality, and outperforms CPLEX in terms of time.

Synergistic Team Composition: A Computational Approach to Foster Diversity in Teams

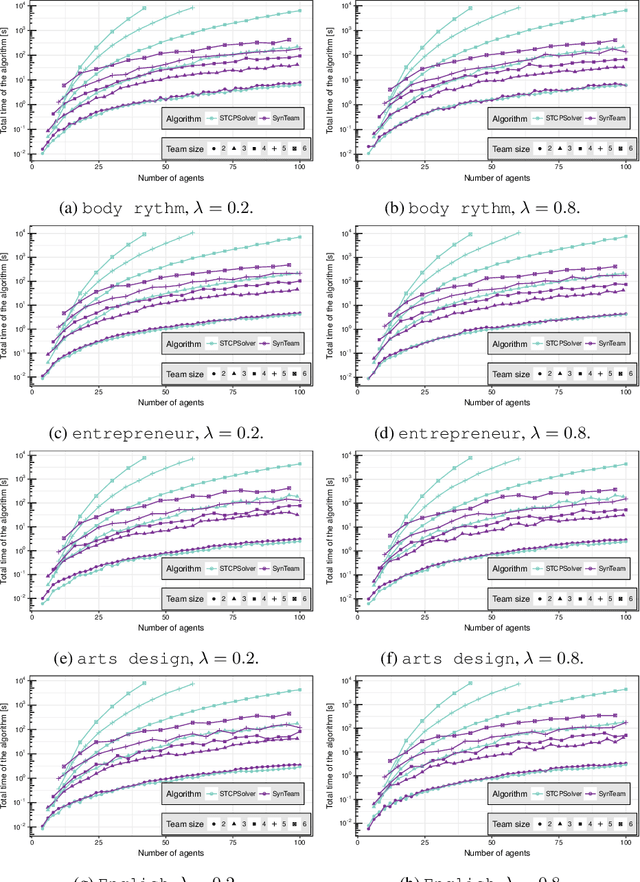
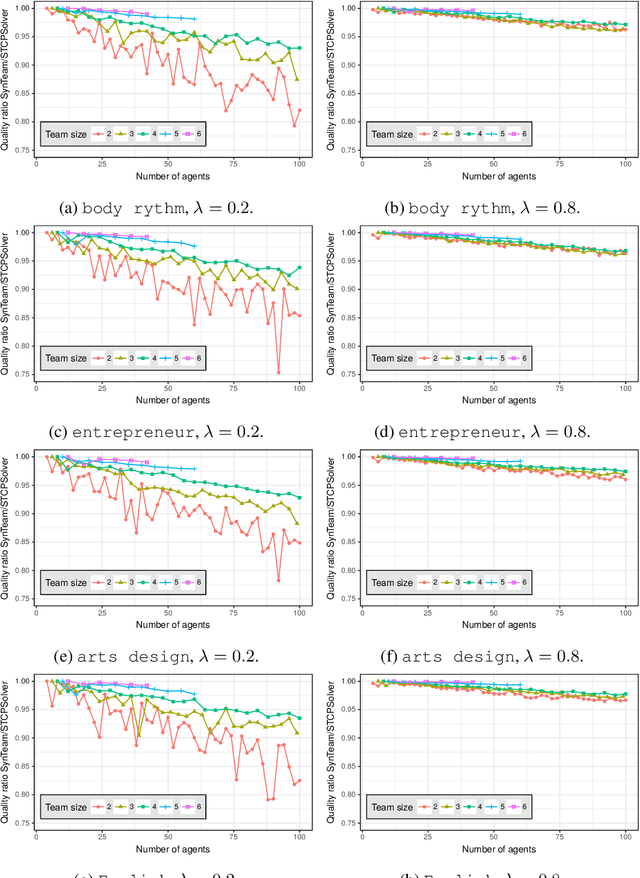
Co-operative learning in heterogeneous teams refers to learning methods in which teams are organised both to accomplish academic tasks and for individuals to gain knowledge. Competencies, personality and the gender of team members are key factors that influence team performance. Here, we introduce a team composition problem, the so-called synergistic team composition problem (STCP), which incorporates such key factors when arranging teams. Thus, the goal of the STCP is to partition a set of individuals into a set of synergistic teams: teams that are diverse in personality and gender and whose members cover all required competencies to complete a task. Furthermore, the STCP requires that all teams are balanced in that they are expected to exhibit similar performances when completing the task. We propose two efficient algorithms to solve the STCP. Our first algorithm is based on a linear programming formulation and is appropriate to solve small instances of the problem. Our second algorithm is an anytime heuristic that is effective for large instances of the STCP. Finally, we thoroughly study the computational properties of both algorithms in an educational context when grouping students in a classroom into teams using actual-world data.

Improving Max-Sum through Decimation to Solve Loopy Distributed Constraint Optimization Problems

In the context of solving large distributed constraint optimization problems (DCOP), belief-propagation and approximate inference algorithms are candidates of choice. However, in general, when the factor graph is very loopy (i.e. cyclic), these solution methods suffer from bad performance, due to non-convergence and many exchanged messages. As to improve performances of the Max-Sum inference algorithm when solving loopy constraint optimization problems, we propose here to take inspiration from the belief-propagation-guided dec-imation used to solve sparse random graphs (k-satisfiability). We propose the novel DeciMaxSum method, which is parameterized in terms of policies to decide when to trigger decimation, which variables to decimate, and which values to assign to decimated variables. Based on an empirical evaluation on a classical BP benchmark (the Ising model), some of these combinations of policies exhibit better performance than state-of-the-art competitors.

Algorithms for Graph-Constrained Coalition Formation in the Real World

Coalition formation typically involves the coming together of multiple, heterogeneous, agents to achieve both their individual and collective goals. In this paper, we focus on a special case of coalition formation known as Graph-Constrained Coalition Formation (GCCF) whereby a network connecting the agents constrains the formation of coalitions. We focus on this type of problem given that in many real-world applications, agents may be connected by a communication network or only trust certain peers in their social network. We propose a novel representation of this problem based on the concept of edge contraction, which allows us to model the search space induced by the GCCF problem as a rooted tree. Then, we propose an anytime solution algorithm (CFSS), which is particularly efficient when applied to a general class of characteristic functions called $m+a$ functions. Moreover, we show how CFSS can be efficiently parallelised to solve GCCF using a non-redundant partition of the search space. We benchmark CFSS on both synthetic and realistic scenarios, using a real-world dataset consisting of the energy consumption of a large number of households in the UK. Our results show that, in the best case, the serial version of CFSS is 4 orders of magnitude faster than the state of the art, while the parallel version is 9.44 times faster than the serial version on a 12-core machine. Moreover, CFSS is the first approach to provide anytime approximate solutions with quality guarantees for very large systems of agents (i.e., with more than 2700 agents).