Factorizers for Distributed Sparse Block Codes

Distributed sparse block codes (SBCs) exhibit compact representations for encoding and manipulating symbolic data structures using fixed-with vectors. One major challenge however is to disentangle, or factorize, such data structures into their constituent elements without having to search through all possible combinations. This factorization becomes more challenging when queried by noisy SBCs wherein symbol representations are relaxed due to perceptual uncertainty and approximations made when modern neural networks are used to generate the query vectors. To address these challenges, we first propose a fast and highly accurate method for factorizing a more flexible and hence generalized form of SBCs, dubbed GSBCs. Our iterative factorizer introduces a threshold-based nonlinear activation, a conditional random sampling, and an $\ell_\infty$-based similarity metric. Its random sampling mechanism in combination with the search in superposition allows to analytically determine the expected number of decoding iterations, which matches the empirical observations up to the GSBC's bundling capacity. Secondly, the proposed factorizer maintains its high accuracy when queried by noisy product vectors generated using deep convolutional neural networks (CNNs). This facilitates its application in replacing the large fully connected layer (FCL) in CNNs, whereby C trainable class vectors, or attribute combinations, can be implicitly represented by our factorizer having F-factor codebooks, each with $\sqrt[\leftroot{-2}\uproot{2}F]{C}$ fixed codevectors. We provide a methodology to flexibly integrate our factorizer in the classification layer of CNNs with a novel loss function. We demonstrate the feasibility of our method on four deep CNN architectures over CIFAR-100, ImageNet-1K, and RAVEN datasets. In all use cases, the number of parameters and operations are significantly reduced compared to the FCL.

In-memory factorization of holographic perceptual representations

Disentanglement of constituent factors of a sensory signal is central to perception and cognition and hence is a critical task for future artificial intelligence systems. In this paper, we present a compute engine capable of efficiently factorizing holographic perceptual representations by exploiting the computation-in-superposition capability of brain-inspired hyperdimensional computing and the intrinsic stochasticity associated with analog in-memory computing based on nanoscale memristive devices. Such an iterative in-memory factorizer is shown to solve at least five orders of magnitude larger problems that cannot be solved otherwise, while also significantly lowering the computational time and space complexity. We present a large-scale experimental demonstration of the factorizer by employing two in-memory compute chips based on phase-change memristive devices. The dominant matrix-vector multiply operations are executed at O(1) thus reducing the computational time complexity to merely the number of iterations. Moreover, we experimentally demonstrate the ability to factorize visual perceptual representations reliably and efficiently.

In-memory Realization of In-situ Few-shot Continual Learning with a Dynamically Evolving Explicit Memory

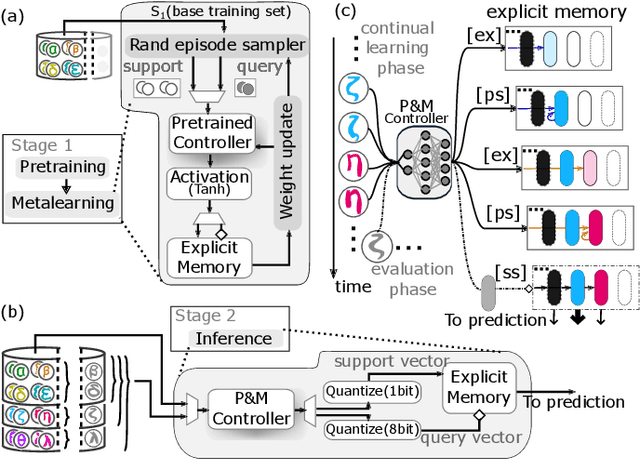
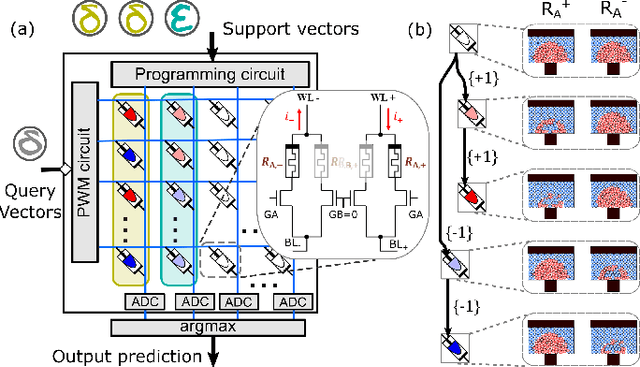
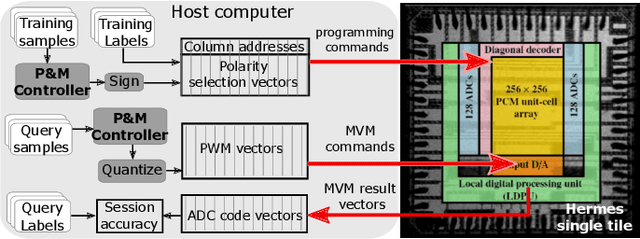
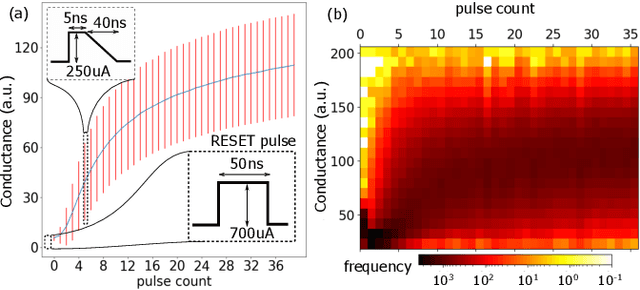
Continually learning new classes from a few training examples without forgetting previous old classes demands a flexible architecture with an inevitably growing portion of storage, in which new examples and classes can be incrementally stored and efficiently retrieved. One viable architectural solution is to tightly couple a stationary deep neural network to a dynamically evolving explicit memory (EM). As the centerpiece of this architecture, we propose an EM unit that leverages energy-efficient in-memory compute (IMC) cores during the course of continual learning operations. We demonstrate for the first time how the EM unit can physically superpose multiple training examples, expand to accommodate unseen classes, and perform similarity search during inference, using operations on an IMC core based on phase-change memory (PCM). Specifically, the physical superposition of a few encoded training examples is realized via in-situ progressive crystallization of PCM devices. The classification accuracy achieved on the IMC core remains within a range of 1.28%--2.5% compared to that of the state-of-the-art full-precision baseline software model on both the CIFAR-100 and miniImageNet datasets when continually learning 40 novel classes (from only five examples per class) on top of 60 old classes.