Neural Architecture Search without Training

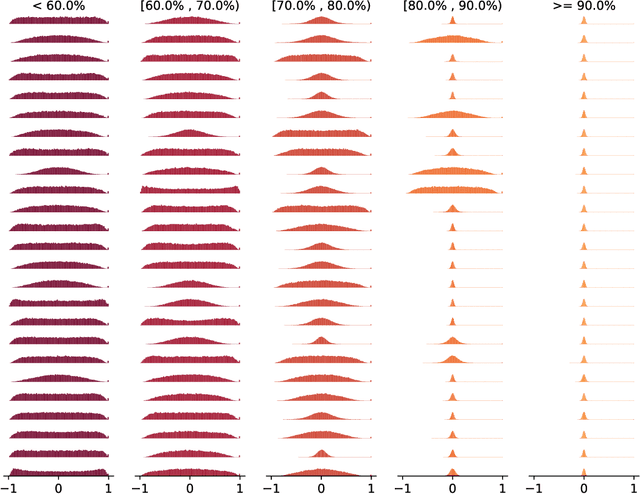
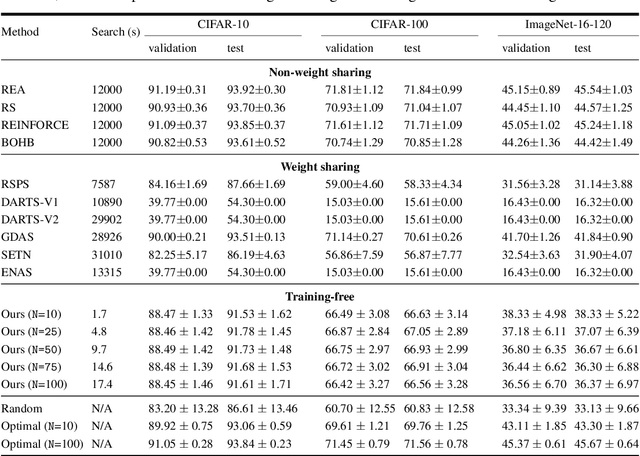
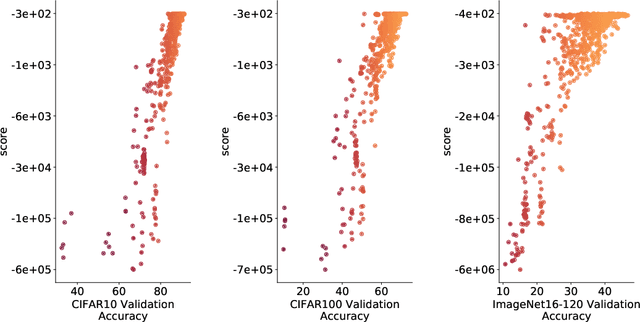
The time and effort involved in hand-designing deep neural networks is immense. This has prompted the development of Neural Architecture Search (NAS) techniques to automate this design. However, NAS algorithms tend to be extremely slow and expensive; they need to train vast numbers of candidate networks to inform the search process. This could be remedied if we could infer a network's trained accuracy from its initial state. In this work, we examine how the linear maps induced by data points correlate for untrained network architectures in the NAS-Bench-201 search space, and motivate how this can be used to give a measure of modelling flexibility which is highly indicative of a network's trained performance. We incorporate this measure into a simple algorithm that allows us to search for powerful networks without any training in a matter of seconds on a single GPU. Code to reproduce our experiments is available at https://github.com/BayesWatch/nas-without-training.

Better Boosting with Bandits for Online Learning

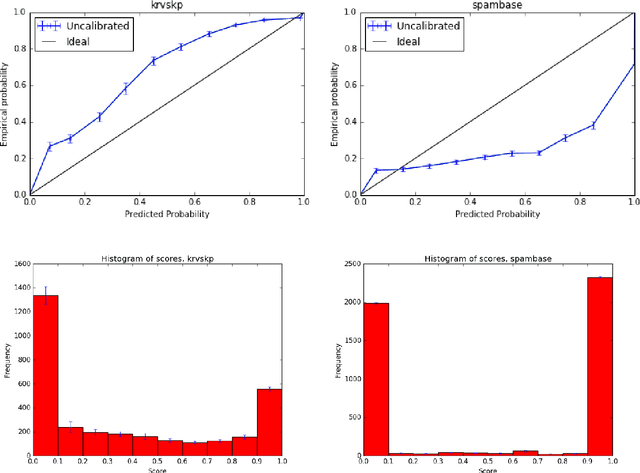
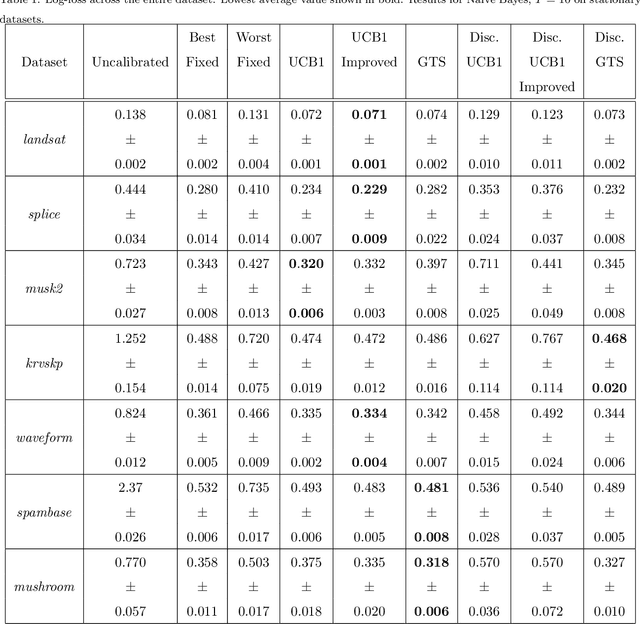
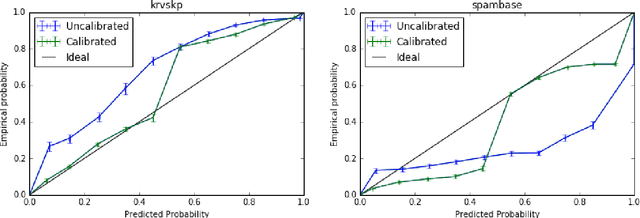
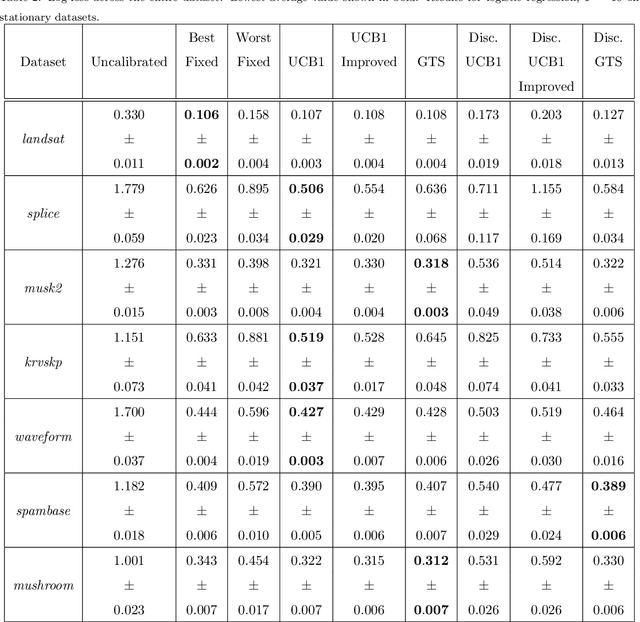
Probability estimates generated by boosting ensembles are poorly calibrated because of the margin maximization nature of the algorithm. The outputs of the ensemble need to be properly calibrated before they can be used as probability estimates. In this work, we demonstrate that online boosting is also prone to producing distorted probability estimates. In batch learning, calibration is achieved by reserving part of the training data for training the calibrator function. In the online setting, a decision needs to be made on each round: shall the new example(s) be used to update the parameters of the ensemble or those of the calibrator. We proceed to resolve this decision with the aid of bandit optimization algorithms. We demonstrate superior performance to uncalibrated and naively-calibrated on-line boosting ensembles in terms of probability estimation. Our proposed mechanism can be easily adapted to other tasks(e.g. cost-sensitive classification) and is robust to the choice of hyperparameters of both the calibrator and the ensemble.

Thompson Sampling in Switching Environments with Bayesian Online Change Point Detection

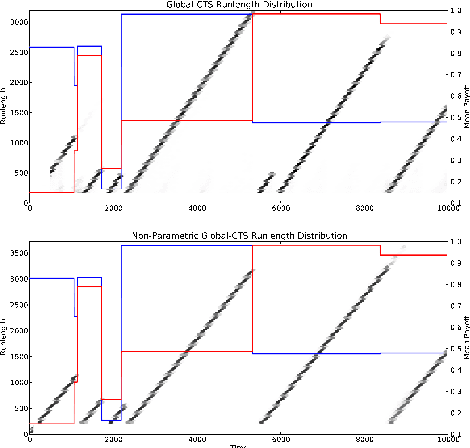
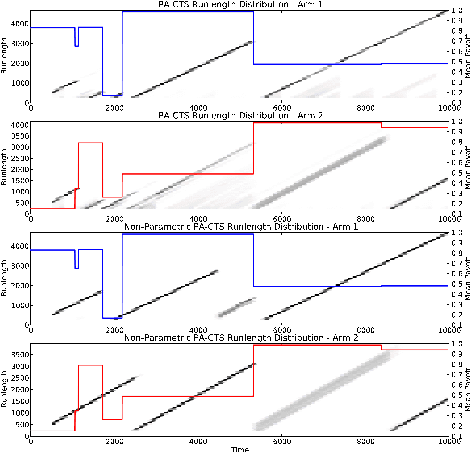
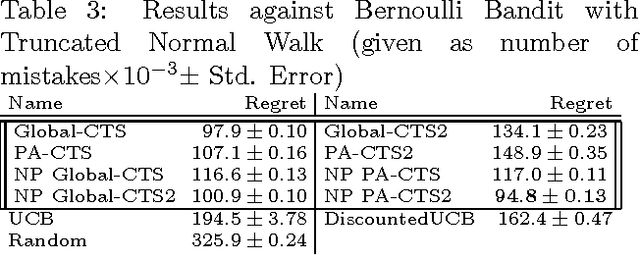
Thompson Sampling has recently been shown to be optimal in the Bernoulli Multi-Armed Bandit setting[Kaufmann et al., 2012]. This bandit problem assumes stationary distributions for the rewards. It is often unrealistic to model the real world as a stationary distribution. In this paper we derive and evaluate algorithms using Thompson Sampling for a Switching Multi-Armed Bandit Problem. We propose a Thompson Sampling strategy equipped with a Bayesian change point mechanism to tackle this problem. We develop algorithms for a variety of cases with constant switching rate: when switching occurs all arms change (Global Switching), switching occurs independently for each arm (Per-Arm Switching), when the switching rate is known and when it must be inferred from data. This leads to a family of algorithms we collectively term Change-Point Thompson Sampling (CTS). We show empirical results of the algorithm in 4 artificial environments, and 2 derived from real world data; news click-through[Yahoo!, 2011] and foreign exchange data[Dukascopy, 2012], comparing them to some other bandit algorithms. In real world data CTS is the most effective.