Thompson Sampling in Switching Environments with Bayesian Online Change Point Detection
Paper and Code
Feb 15, 2013

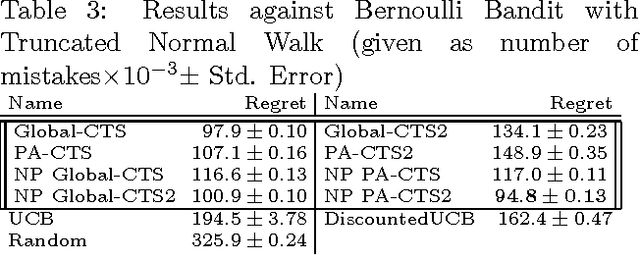
Thompson Sampling has recently been shown to be optimal in the Bernoulli Multi-Armed Bandit setting[Kaufmann et al., 2012]. This bandit problem assumes stationary distributions for the rewards. It is often unrealistic to model the real world as a stationary distribution. In this paper we derive and evaluate algorithms using Thompson Sampling for a Switching Multi-Armed Bandit Problem. We propose a Thompson Sampling strategy equipped with a Bayesian change point mechanism to tackle this problem. We develop algorithms for a variety of cases with constant switching rate: when switching occurs all arms change (Global Switching), switching occurs independently for each arm (Per-Arm Switching), when the switching rate is known and when it must be inferred from data. This leads to a family of algorithms we collectively term Change-Point Thompson Sampling (CTS). We show empirical results of the algorithm in 4 artificial environments, and 2 derived from real world data; news click-through[Yahoo!, 2011] and foreign exchange data[Dukascopy, 2012], comparing them to some other bandit algorithms. In real world data CTS is the most effective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge