ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

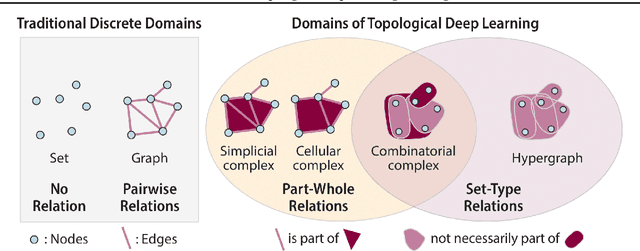
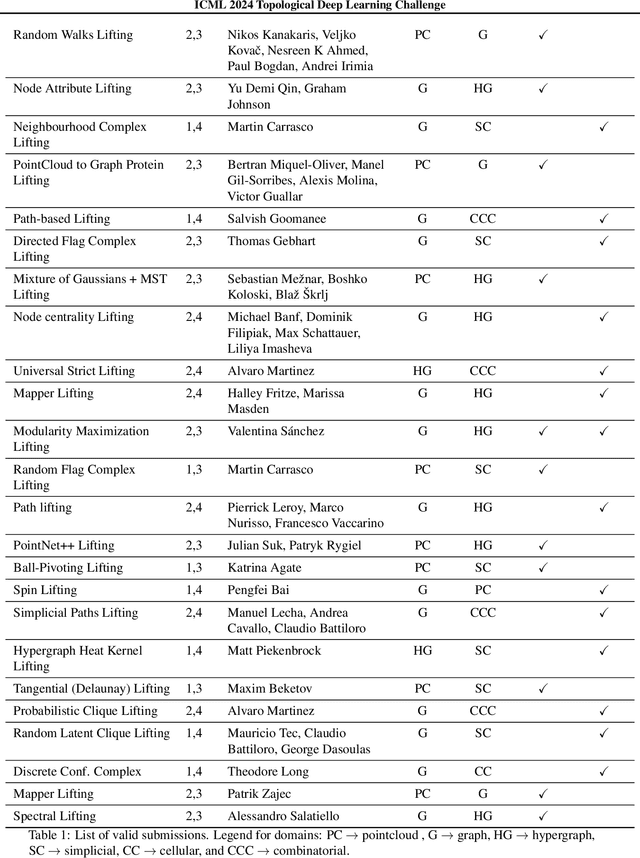
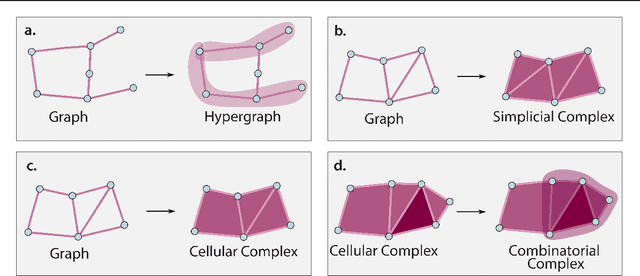
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Isometric Representations in Neural Networks Improve Robustness

Artificial and biological agents cannon learn given completely random and unstructured data. The structure of data is encoded in the metric relationships between data points. In the context of neural networks, neuronal activity within a layer forms a representation reflecting the transformation that the layer implements on its inputs. In order to utilize the structure in the data in a truthful manner, such representations should reflect the input distances and thus be continuous and isometric. Supporting this statement, recent findings in neuroscience propose that generalization and robustness are tied to neural representations being continuously differentiable. In machine learning, most algorithms lack robustness and are generally thought to rely on aspects of the data that differ from those that humans use, as is commonly seen in adversarial attacks. During cross-entropy classification, the metric and structural properties of network representations are usually broken both between and within classes. This side effect from training can lead to instabilities under perturbations near locations where such structure is not preserved. One of the standard solutions to obtain robustness is to add ad hoc regularization terms, but to our knowledge, forcing representations to preserve the metric structure of the input data as a stabilising mechanism has not yet been studied. In this work, we train neural networks to perform classification while simultaneously maintaining within-class metric structure, leading to isometric within-class representations. Such network representations turn out to be beneficial for accurate and robust inference. By stacking layers with this property we create a network architecture that facilitates hierarchical manipulation of internal neural representations. Finally, we verify that isometric regularization improves the robustness to adversarial attacks on MNIST.