John S. Breese
Decision-Theoretic Troubleshooting: A Framework for Repair and Experiment
May 17, 2015

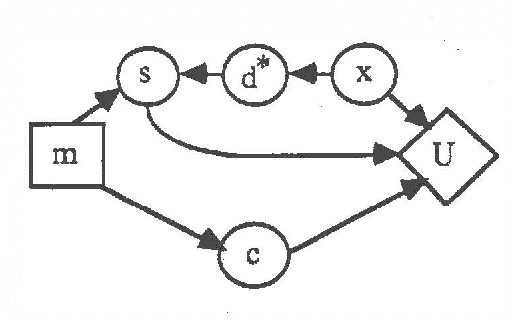
Abstract:We develop and extend existing decision-theoretic methods for troubleshooting a nonfunctioning device. Traditionally, diagnosis with Bayesian networks has focused on belief updating---determining the probabilities of various faults given current observations. In this paper, we extend this paradigm to include taking actions. In particular, we consider three classes of actions: (1) we can make observations regarding the behavior of a device and infer likely faults as in traditional diagnosis, (2) we can repair a component and then observe the behavior of the device to infer likely faults, and (3) we can change the configuration of the device, observe its new behavior, and infer the likelihood of faults. Analysis of latter two classes of troubleshooting actions requires incorporating notions of persistence into the belief-network formalism used for probabilistic inference.
A New Look at Causal Independence
May 17, 2015



Abstract:Heckerman (1993) defined causal independence in terms of a set of temporal conditional independence statements. These statements formalized certain types of causal interaction where (1) the effect is independent of the order that causes are introduced and (2) the impact of a single cause on the effect does not depend on what other causes have previously been applied. In this paper, we introduce an equivalent a temporal characterization of causal independence based on a functional representation of the relationship between causes and the effect. In this representation, the interaction between causes and effect can be written as a nested decomposition of functions. Causal independence can be exploited by representing this decomposition in the belief network, resulting in representations that are more efficient for inference than general causal models. We present empirical results showing the benefits of a causal-independence representation for belief-network inference.
Exact Reasoning Under Uncertainty
Mar 27, 2013Abstract:This paper focuses on designing expert systems to support decision making in complex, uncertain environments. In this context, our research indicates that strictly probabilistic representations, which enable the use of decision-theoretic reasoning, are highly preferable to recently proposed alternatives (e.g., fuzzy set theory and Dempster-Shafer theory). Furthermore, we discuss the language of influence diagrams and a corresponding methodology -decision analysis -- that allows decision theory to be used effectively and efficiently as a decision-making aid. Finally, we use RACHEL, a system that helps infertile couples select medical treatments, to illustrate the methodology of decision analysis as basis for expert decision systems.
Integrating Logical and Probabilistic Reasoning for Decision Making
Mar 27, 2013
Abstract:We describe a representation and a set of inference methods that combine logic programming techniques with probabilistic network representations for uncertainty (influence diagrams). The techniques emphasize the dynamic construction and solution of probabilistic and decision-theoretic models for complex and uncertain domains. Given a query, a logical proof is produced if possible; if not, an influence diagram based on the query and the knowledge of the decision domain is produced and subsequently solved. A uniform declarative, first-order, knowledge representation is combined with a set of integrated inference procedures for logical, probabilistic, and decision-theoretic reasoning.
Decision-Theoretic Control of Problem Solving: Principles and Architecture
Mar 27, 2013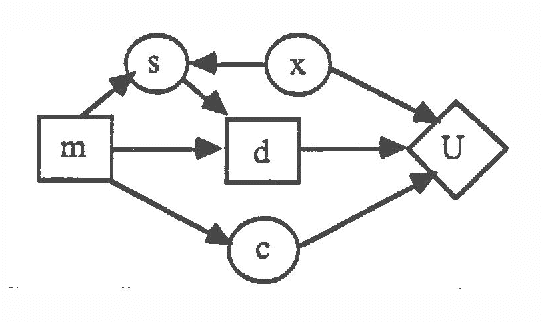
Abstract:This paper presents an approach to the design of autonomous, real-time systems operating in uncertain environments. We address issues of problem solving and reflective control of reasoning under uncertainty in terms of two fundamental elements: l) a set of decision-theoretic models for selecting among alternative problem-solving methods and 2) a general computational architecture for resource-bounded problem solving. The decisiontheoretic models provide a set of principles for choosing among alternative problem-solving methods based on their relative costs and benefits, where benefits are characterized in terms of the value of information provided by the output of a reasoning activity. The output may be an estimate of some uncertain quantity or a recommendation for action. The computational architecture, called Schemer-ll, provides for interleaving of and communication among various problem-solving subsystems. These subsystems provide alternative approaches to information gathering, belief refinement, solution construction, and solution execution. In particular, the architecture provides a mechanism for interrupting the subsystems in response to critical events. We provide a decision theoretic account for scheduling problem-solving elements and for critical-event-driven interruption of activities in an architecture such as Schemer-II.
The Compilation of Decision Models
Mar 27, 2013



Abstract:We introduce and analyze the problem of the compilation of decision models from a decision-theoretic perspective. The techniques described allow us to evaluate various configurations of compiled knowledge given the nature of evidential relationships in a domain, the utilities associated with alternative actions, the costs of run-time delays, and the costs of memory. We describe procedures for selecting a subset of the total observations available to be incorporated into a compiled situation-action mapping, in the context of a binary decision with conditional independence of evidence. The methods allow us to incrementally select the best pieces of evidence to add to the set of compiled knowledge in an engineering setting. After presenting several approaches to compilation, we exercise one of the methods to provide insight into the relationship between the distribution over weights of evidence and the preferred degree of compilation.
Interval Influence Diagrams
Mar 27, 2013



Abstract:We describe a mechanism for performing probabilistic reasoning in influence diagrams using interval rather than point valued probabilities. We derive the procedures for node removal (corresponding to conditional expectation) and arc reversal (corresponding to Bayesian conditioning) in influence diagrams where lower bounds on probabilities are stored at each node. The resulting bounds for the transformed diagram are shown to be optimal within the class of constraints on probability distributions that can be expressed exclusively as lower bounds on the component probabilities of the diagram. Sequences of these operations can be performed to answer probabilistic queries with indeterminacies in the input and for performing sensitivity analysis on an influence diagram. The storage requirements and computational complexity of this approach are comparable to those for point-valued probabilistic inference mechanisms, making the approach attractive for performing sensitivity analysis and where probability information is not available. Limited empirical data on an implementation of the methodology are provided.
IDEAL: A Software Package for Analysis of Influence Diagrams
Mar 27, 2013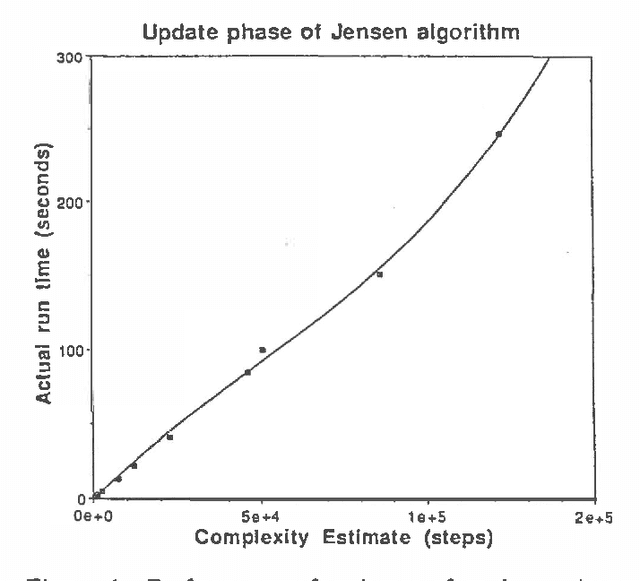
Abstract:IDEAL (Influence Diagram Evaluation and Analysis in Lisp) is a software environment for creation and evaluation of belief networks and influence diagrams. IDEAL is primarily a research tool and provides an implementation of many of the latest developments in belief network and influence diagram evaluation in a unified framework. This paper describes IDEAL and some lessons learned during its development.
Decision Making with Interval Influence Diagrams
Mar 27, 2013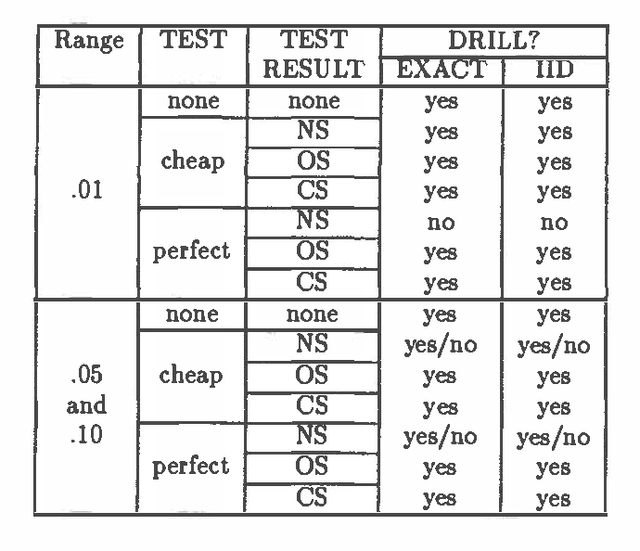
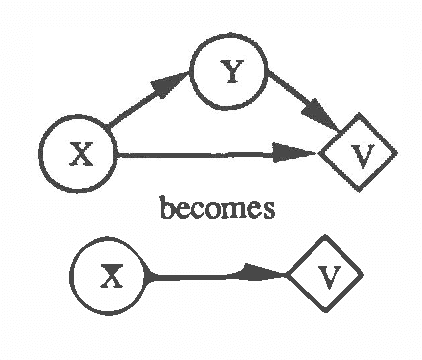

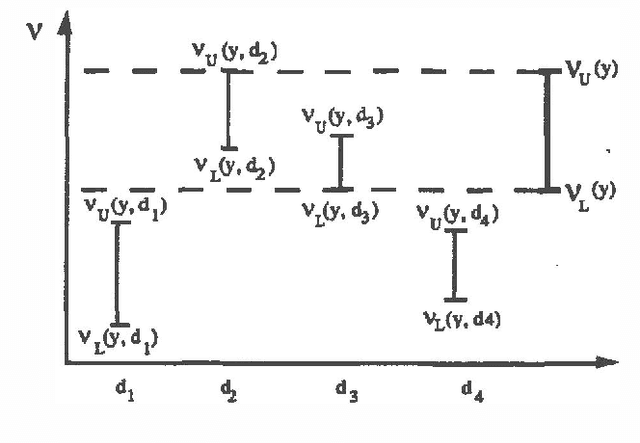
Abstract:In previous work (Fertig and Breese, 1989; Fertig and Breese, 1990) we defined a mechanism for performing probabilistic reasoning in influence diagrams using interval rather than point-valued probabilities. In this paper we extend these procedures to incorporate decision nodes and interval-valued value functions in the diagram. We derive the procedures for chance node removal (calculating expected value) and decision node removal (optimization) in influence diagrams where lower bounds on probabilities are stored at each chance node and interval bounds are stored on the value function associated with the diagram's value node. The output of the algorithm are a set of admissible alternatives for each decision variable and a set of bounds on expected value based on the imprecision in the input. The procedure can be viewed as an approximation to a full e-dimensional sensitivity analysis where n are the number of imprecise probability distributions in the input. We show the transformations are optimal and sound. The performance of the algorithm on an influence diagrams is investigated and compared to an exact algorithm.
Ideal Reformulation of Belief Networks
Mar 27, 2013



Abstract:The intelligent reformulation or restructuring of a belief network can greatly increase the efficiency of inference. However, time expended for reformulation is not available for performing inference. Thus, under time pressure, there is a tradeoff between the time dedicated to reformulating the network and the time applied to the implementation of a solution. We investigate this partition of resources into time applied to reformulation and time used for inference. We shall describe first general principles for computing the ideal partition of resources under uncertainty. These principles have applicability to a wide variety of problems that can be divided into interdependent phases of problem solving. After, we shall present results of our empirical study of the problem of determining the ideal amount of time to devote to searching for clusters in belief networks. In this work, we acquired and made use of probability distributions that characterize (1) the performance of alternative heuristic search methods for reformulating a network instance into a set of cliques, and (2) the time for executing inference procedures on various belief networks. Given a preference model describing the value of a solution as a function of the delay required for its computation, the system selects an ideal time to devote to reformulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge