Automated Construction of Sparse Bayesian Networks from Unstructured Probabilistic Models and Domain Information

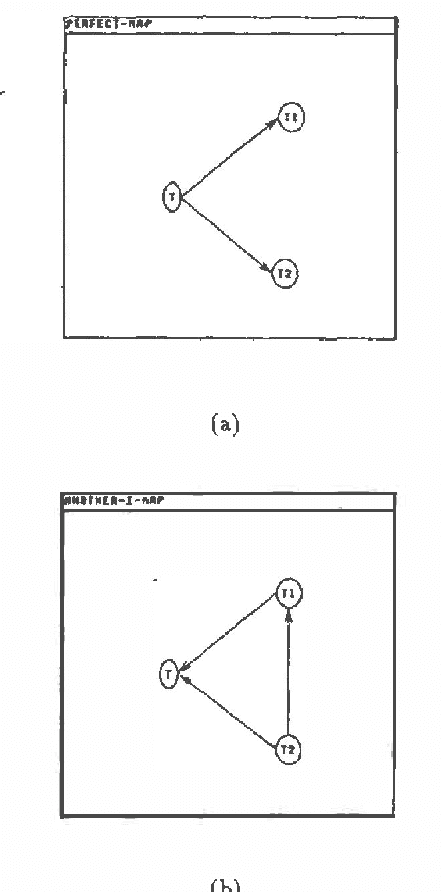
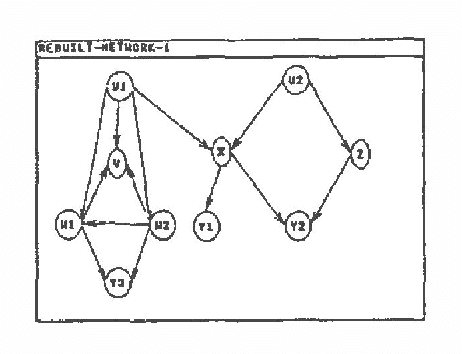
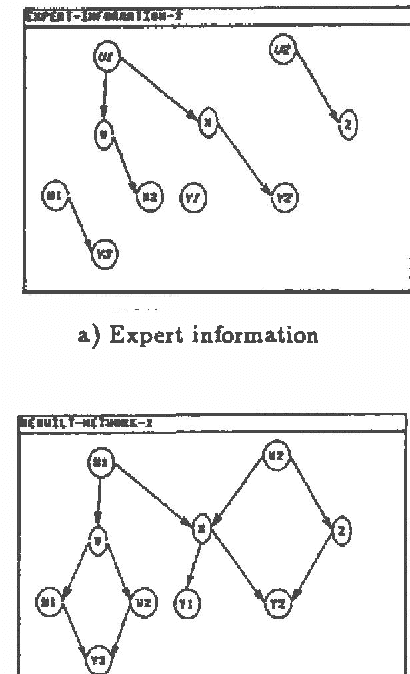
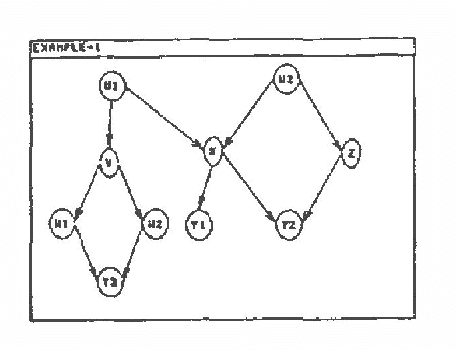
An algorithm for automated construction of a sparse Bayesian network given an unstructured probabilistic model and causal domain information from an expert has been developed and implemented. The goal is to obtain a network that explicitly reveals as much information regarding conditional independence as possible. The network is built incrementally adding one node at a time. The expert's information and a greedy heuristic that tries to keep the number of arcs added at each step to a minimum are used to guide the search for the next node to add. The probabilistic model is a predicate that can answer queries about independencies in the domain. In practice the model can be implemented in various ways. For example, the model could be a statistical independence test operating on empirical data or a deductive prover operating on a set of independence statements about the domain.

IDEAL: A Software Package for Analysis of Influence Diagrams

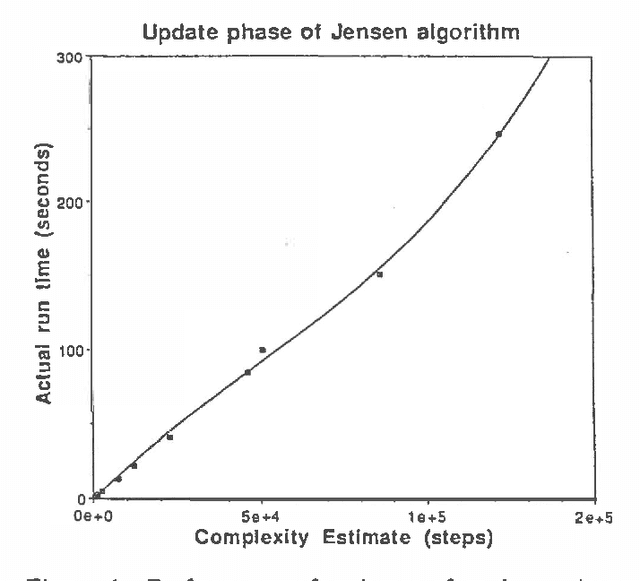
IDEAL (Influence Diagram Evaluation and Analysis in Lisp) is a software environment for creation and evaluation of belief networks and influence diagrams. IDEAL is primarily a research tool and provides an implementation of many of the latest developments in belief network and influence diagram evaluation in a unified framework. This paper describes IDEAL and some lessons learned during its development.

A Generalization of the Noisy-Or Model

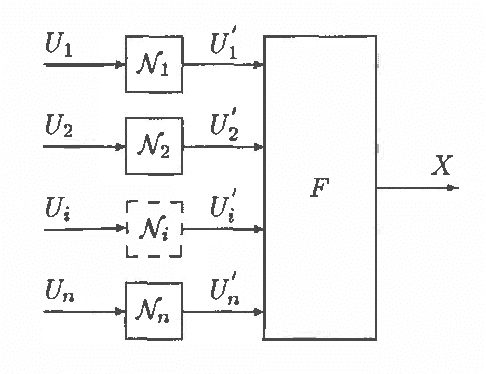
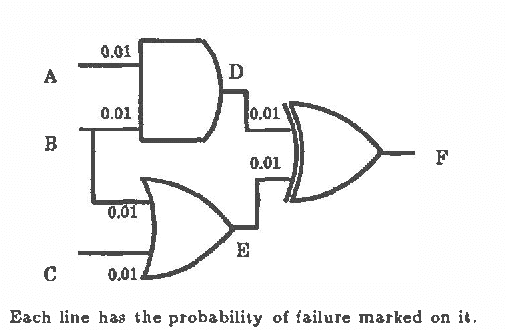
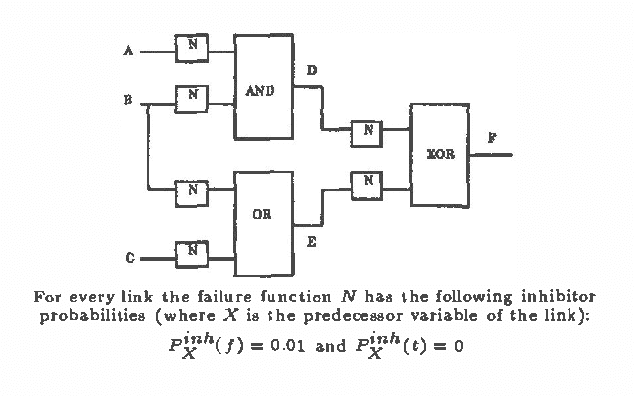
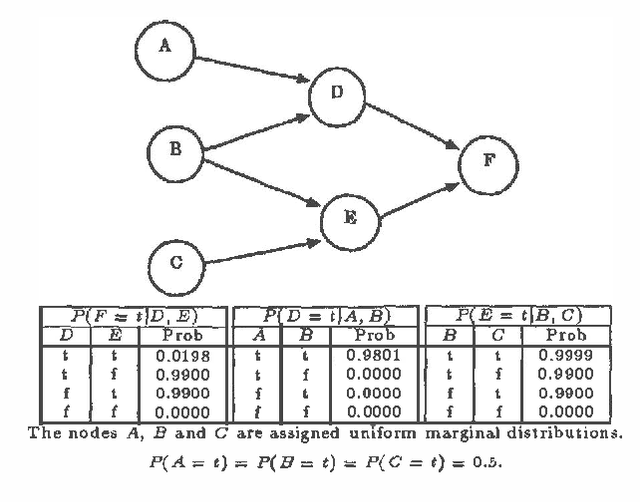
The Noisy-Or model is convenient for describing a class of uncertain relationships in Bayesian networks [Pearl 1988]. Pearl describes the Noisy-Or model for Boolean variables. Here we generalize the model to nary input and output variables and to arbitrary functions other than the Boolean OR function. This generalization is a useful modeling aid for construction of Bayesian networks. We illustrate with some examples including digital circuit diagnosis and network reliability analysis.

A Probabilistic Approach to Hierarchical Model-based Diagnosis

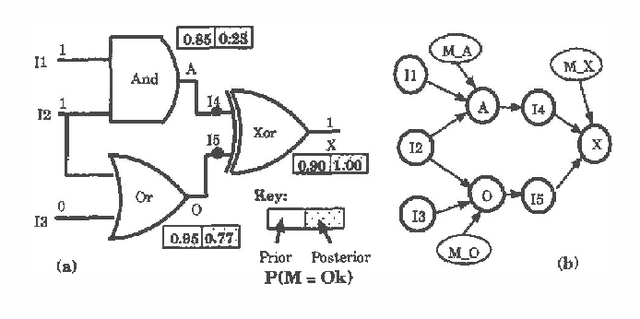
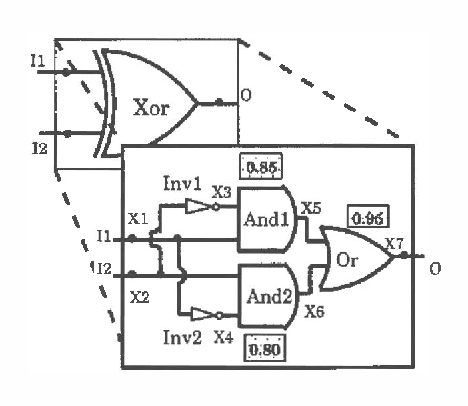
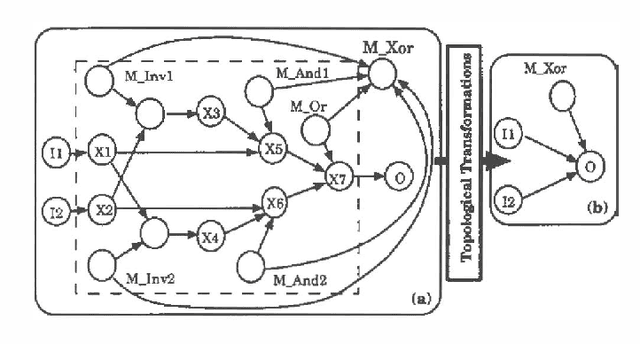
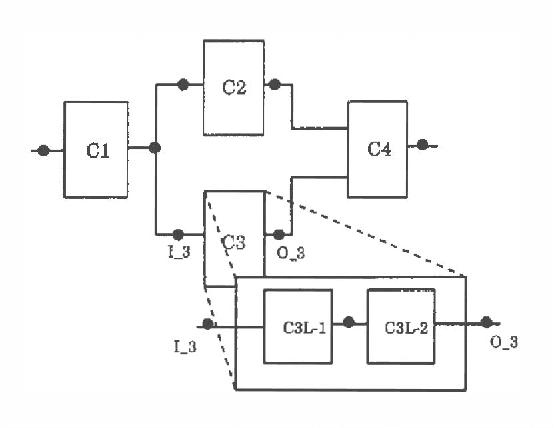
Model-based diagnosis reasons backwards from a functional schematic of a system to isolate faults given observations of anomalous behavior. We develop a fully probabilistic approach to model based diagnosis and extend it to support hierarchical models. Our scheme translates the functional schematic into a Bayesian network and diagnostic inference takes place in the Bayesian network. A Bayesian network diagnostic inference algorithm is modified to take advantage of the hierarchy to give computational gains.

Exploiting System Hierarchy to Compute Repair Plans in Probabilistic Model-based Diagnosis

The goal of model-based diagnosis is to isolate causes of anomalous system behavior and recommend inexpensive repair actions in response. In general, precomputing optimal repair policies is intractable. To date, investigators addressing this problem have explored approximations that either impose restrictions on the system model (such as a single fault assumption) or compute an immediate best action with limited lookahead. In this paper, we develop a formulation of repair in model-based diagnosis and a repair algorithm that computes optimal sequences of actions. This optimal approach is costly but can be applied to precompute an optimal repair strategy for compact systems. We show how we can exploit a hierarchical system specification to make this approach tractable for large systems. When introducing hierarchy, we also consider the tradeoff between simply replacing a component and decomposing it to repair its subcomponents. The hierarchical repair algorithm is suitable for off-line precomputation of an optimal repair strategy. A modification of the algorithm takes advantage of an iterative deepening scheme to trade off inference time and the quality of the computed strategy.

A Polynomial Algorithm for Computing the Optimal Repair Strategy in a System with Independent Component Failures

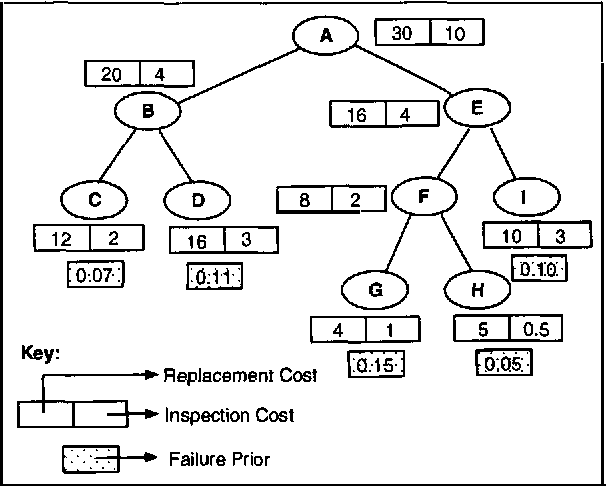
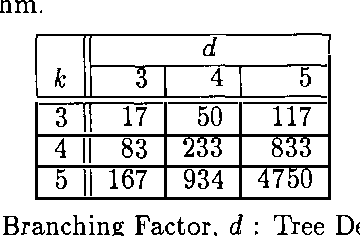
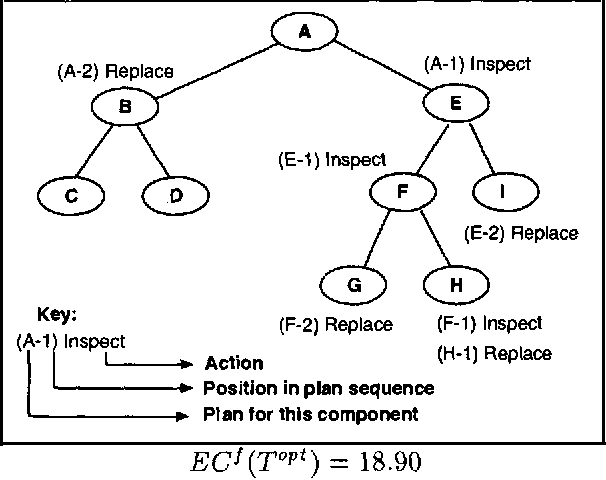
The goal of diagnosis is to compute good repair strategies in response to anomalous system behavior. In a decision theoretic framework, a good repair strategy has low expected cost. In a general formulation of the problem, the computation of the optimal (lowest expected cost) repair strategy for a system with multiple faults is intractable. In this paper, we consider an interesting and natural restriction on the behavior of the system being diagnosed: (a) the system exhibits faulty behavior if and only if one or more components is malfunctioning. (b) The failures of the system components are independent. Given this restriction on system behavior, we develop a polynomial time algorithm for computing the optimal repair strategy. We then go on to introduce a system hierarchy and the notion of inspecting (testing) components before repair. We develop a linear time algorithm for computing an optimal repair strategy for the hierarchical system which includes both repair and inspection.

Modeling Failure Priors and Persistence in Model-Based Diagnosis

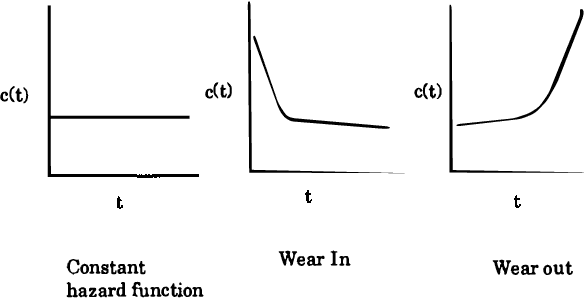
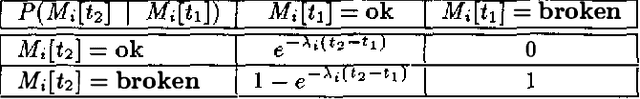
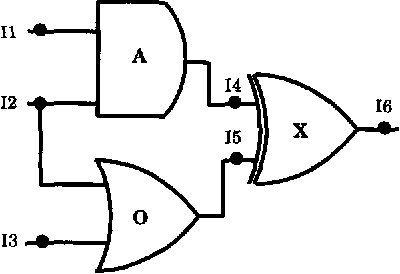
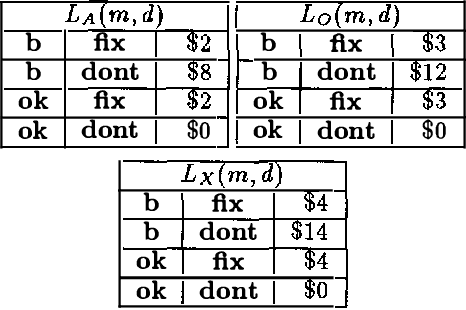
Probabilistic model-based diagnosis computes the posterior probabilities of failure of components from the prior probabilities of component failure and observations of system behavior. One problem with this method is that such priors are almost never directly available. One of the reasons is that the prior probability estimates include an implicit notion of a time interval over which they are specified -- for example, if the probability of failure of a component is 0.05, is this over the period of a day or is this over a week? A second problem facing probabilistic model-based diagnosis is the modeling of persistence. Say we have an observation about a system at time t_1 and then another observation at a later time t_2. To compute posterior probabilities that take into account both the observations, we need some model of how the state of the system changes from time t_1 to t_2. In this paper, we address these problems using techniques from Reliability theory. We show how to compute the failure prior of a component from an empirical measure of its reliability -- the Mean Time Between Failure (MTBF). We also develop a scheme to model persistence when handling multiple time tagged observations.

Efficient Enumeration of Instantiations in Bayesian Networks

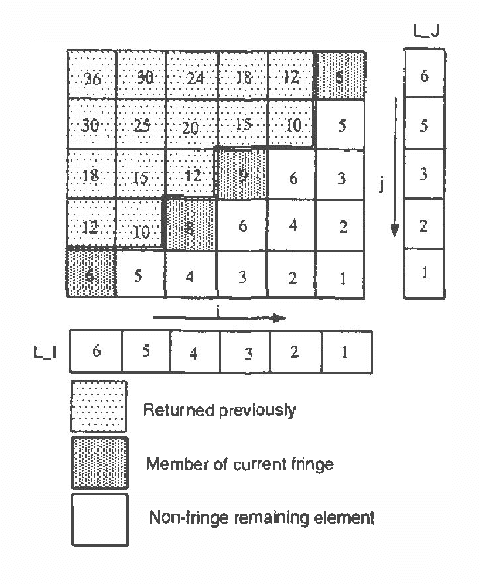
Over the past several years Bayesian networks have been applied to a wide variety of problems. A central problem in applying Bayesian networks is that of finding one or more of the most probable instantiations of a network. In this paper we develop an efficient algorithm that incrementally enumerates the instantiations of a Bayesian network in decreasing order of probability. Such enumeration algorithms are applicable in a variety of applications ranging from medical expert systems to model-based diagnosis. Fundamentally, our algorithm is simply performing a lazy enumeration of the sorted list of all instantiations of the network. This insight leads to a very concise algorithm statement which is both easily understood and implemented. We show that for singly connected networks, our algorithm generates the next instantiation in time polynomial in the size of the network. The algorithm extends to arbitrary Bayesian networks using standard conditioning techniques. We empirically evaluate the enumeration algorithm and demonstrate its practicality.