Energy-efficiency Limits on Training AI Systems using Learning-in-Memory

Learning-in-memory (LIM) is a recently proposed paradigm to overcome fundamental memory bottlenecks in training machine learning systems. While compute-in-memory (CIM) approaches can address the so-called memory-wall (i.e. energy dissipated due to repeated memory read access) they are agnostic to the energy dissipated due to repeated memory writes at the precision required for training (the update-wall), and they don't account for the energy dissipated when transferring information between short-term and long-term memories (the consolidation-wall). The LIM paradigm proposes that these bottlenecks, too, can be overcome if the energy barrier of physical memories is adaptively modulated such that the dynamics of memory updates and consolidation match the Lyapunov dynamics of gradient-descent training of an AI model. In this paper, we derive new theoretical lower bounds on energy dissipation when training AI systems using different LIM approaches. The analysis presented here is model-agnostic and highlights the trade-off between energy efficiency and the speed of training. The resulting non-equilibrium energy-efficiency bounds have a similar flavor as that of Landauer's energy-dissipation bounds. We also extend these limits by taking into account the number of floating-point operations (FLOPs) used for training, the size of the AI model, and the precision of the training parameters. Our projections suggest that the energy-dissipation lower-bound to train a brain scale AI system (comprising of $10^{15}$ parameters) using LIM is $10^8 \sim 10^9$ Joules, which is on the same magnitude the Landauer's adiabatic lower-bound and $6$ to $7$ orders of magnitude lower than the projections obtained using state-of-the-art AI accelerator hardware lower-bounds.

Towards Chip-in-the-loop Spiking Neural Network Training via Metropolis-Hastings Sampling

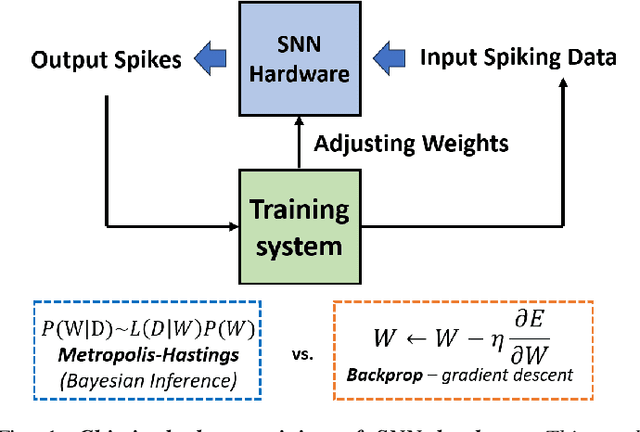
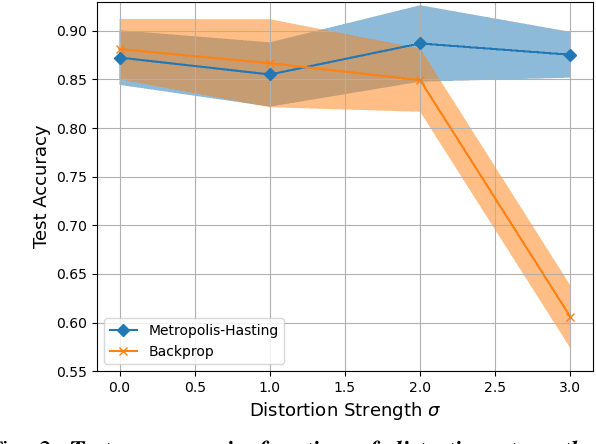
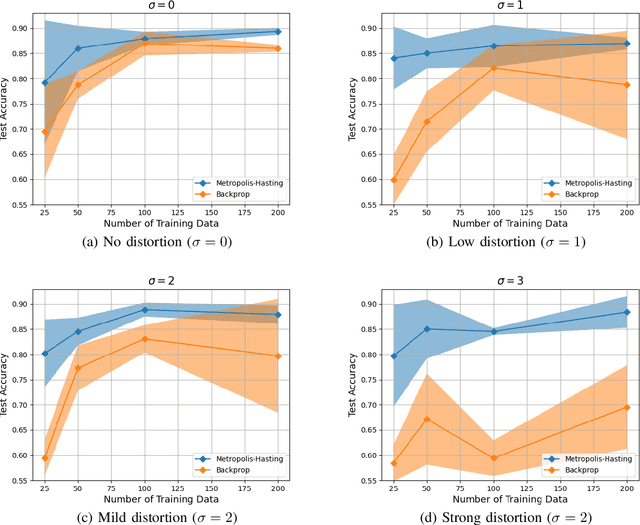
This paper studies the use of Metropolis-Hastings sampling for training Spiking Neural Network (SNN) hardware subject to strong unknown non-idealities, and compares the proposed approach to the common use of the backpropagation of error (backprop) algorithm and surrogate gradients, widely used to train SNNs in literature. Simulations are conducted within a chip-in-the-loop training context, where an SNN subject to unknown distortion must be trained to detect cancer from measurements, within a biomedical application context. Our results show that the proposed approach strongly outperforms the use of backprop by up to $27\%$ higher accuracy when subject to strong hardware non-idealities. Furthermore, our results also show that the proposed approach outperforms backprop in terms of SNN generalization, needing $>10 \times$ less training data for achieving effective accuracy. These findings make the proposed training approach well-suited for SNN implementations in analog subthreshold circuits and other emerging technologies where unknown hardware non-idealities can jeopardize backprop.