Perfecting Depth: Uncertainty-Aware Enhancement of Metric Depth

We propose a novel two-stage framework for sensor depth enhancement, called Perfecting Depth. This framework leverages the stochastic nature of diffusion models to automatically detect unreliable depth regions while preserving geometric cues. In the first stage (stochastic estimation), the method identifies unreliable measurements and infers geometric structure by leveraging a training-inference domain gap. In the second stage (deterministic refinement), it enforces structural consistency and pixel-level accuracy using the uncertainty map derived from the first stage. By combining stochastic uncertainty modeling with deterministic refinement, our method yields dense, artifact-free depth maps with improved reliability. Experimental results demonstrate its effectiveness across diverse real-world scenarios. Furthermore, theoretical analysis, various experiments, and qualitative visualizations validate its robustness and scalability. Our framework sets a new baseline for sensor depth enhancement, with potential applications in autonomous driving, robotics, and immersive technologies.

Masked Spatial Propagation Network for Sparsity-Adaptive Depth Refinement

The main function of depth completion is to compensate for an insufficient and unpredictable number of sparse depth measurements of hardware sensors. However, existing research on depth completion assumes that the sparsity -- the number of points or LiDAR lines -- is fixed for training and testing. Hence, the completion performance drops severely when the number of sparse depths changes significantly. To address this issue, we propose the sparsity-adaptive depth refinement (SDR) framework, which refines monocular depth estimates using sparse depth points. For SDR, we propose the masked spatial propagation network (MSPN) to perform SDR with a varying number of sparse depths effectively by gradually propagating sparse depth information throughout the entire depth map. Experimental results demonstrate that MPSN achieves state-of-the-art performance on both SDR and conventional depth completion scenarios.

Versatile Depth Estimator Based on Common Relative Depth Estimation and Camera-Specific Relative-to-Metric Depth Conversion

A typical monocular depth estimator is trained for a single camera, so its performance drops severely on images taken with different cameras. To address this issue, we propose a versatile depth estimator (VDE), composed of a common relative depth estimator (CRDE) and multiple relative-to-metric converters (R2MCs). The CRDE extracts relative depth information, and each R2MC converts the relative information to predict metric depths for a specific camera. The proposed VDE can cope with diverse scenes, including both indoor and outdoor scenes, with only a 1.12\% parameter increase per camera. Experimental results demonstrate that VDE supports multiple cameras effectively and efficiently and also achieves state-of-the-art performance in the conventional single-camera scenario.

Depth Map Decomposition for Monocular Depth Estimation

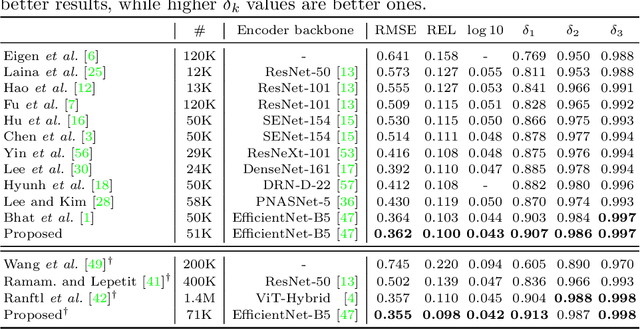
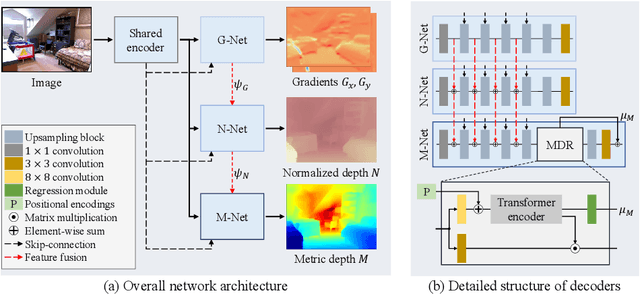
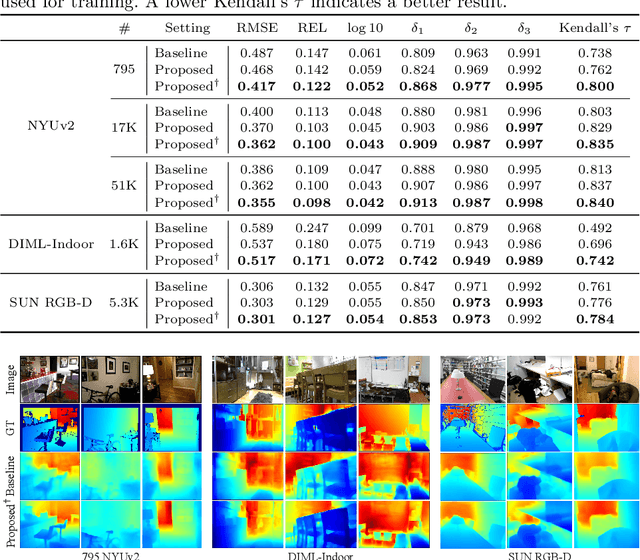
We propose a novel algorithm for monocular depth estimation that decomposes a metric depth map into a normalized depth map and scale features. The proposed network is composed of a shared encoder and three decoders, called G-Net, N-Net, and M-Net, which estimate gradient maps, a normalized depth map, and a metric depth map, respectively. M-Net learns to estimate metric depths more accurately using relative depth features extracted by G-Net and N-Net. The proposed algorithm has the advantage that it can use datasets without metric depth labels to improve the performance of metric depth estimation. Experimental results on various datasets demonstrate that the proposed algorithm not only provides competitive performance to state-of-the-art algorithms but also yields acceptable results even when only a small amount of metric depth data is available for its training.