Non-Euclidean Spatial Graph Neural Network

Spatial networks are networks whose graph topology is constrained by their embedded spatial space. Understanding the coupled spatial-graph properties is crucial for extracting powerful representations from spatial networks. Therefore, merely combining individual spatial and network representations cannot reveal the underlying interaction mechanism of spatial networks. Besides, existing spatial network representation learning methods can only consider networks embedded in Euclidean space, and can not well exploit the rich geometric information carried by irregular and non-uniform non-Euclidean space. In order to address this issue, in this paper we propose a novel generic framework to learn the representation of spatial networks that are embedded in non-Euclidean manifold space. Specifically, a novel message-passing-based neural network is proposed to combine graph topology and spatial geometry, where spatial geometry is extracted as messages on the edges. We theoretically guarantee that the learned representations are provably invariant to important symmetries such as rotation or translation, and simultaneously maintain sufficient ability in distinguishing different geometric structures. The strength of our proposed method is demonstrated through extensive experiments on both synthetic and real-world datasets.

Parameter Convex Neural Networks

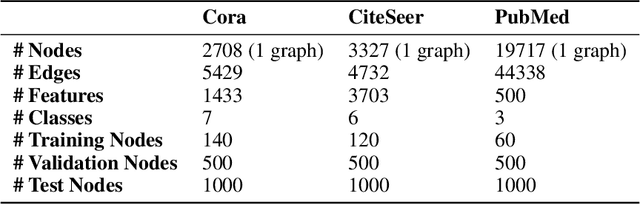
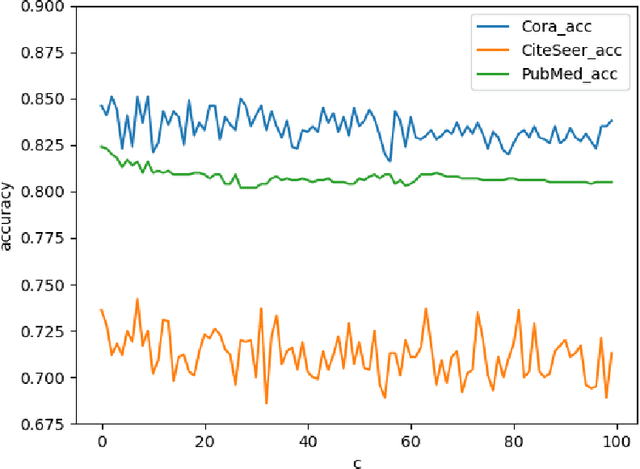
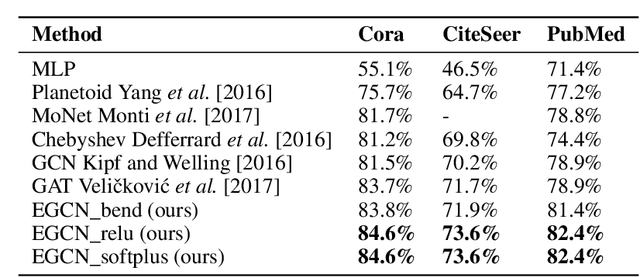
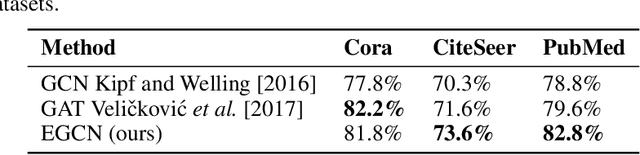
Deep learning utilizing deep neural networks (DNNs) has achieved a lot of success recently in many important areas such as computer vision, natural language processing, and recommendation systems. The lack of convexity for DNNs has been seen as a major disadvantage of many optimization methods, such as stochastic gradient descent, which greatly reduces the genelization of neural network applications. We realize that the convexity make sense in the neural network and propose the exponential multilayer neural network (EMLP), a class of parameter convex neural network (PCNN) which is convex with regard to the parameters of the neural network under some conditions that can be realized. Besides, we propose the convexity metric for the two-layer EGCN and test the accuracy when the convexity metric changes. For late experiments, we use the same architecture to make the exponential graph convolutional network (EGCN) and do the experiment on the graph classificaion dataset in which our model EGCN performs better than the graph convolutional network (GCN) and the graph attention network (GAT).

Research of Damped Newton Stochastic Gradient Descent Method for Neural Network Training

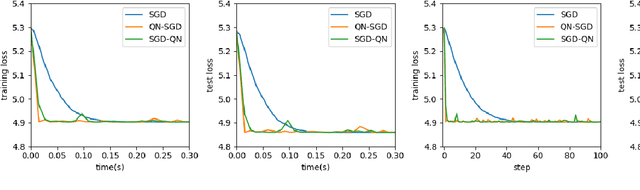
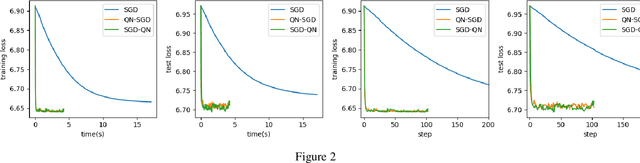
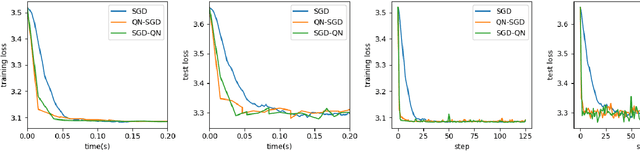
First-order methods like stochastic gradient descent(SGD) are recently the popular optimization method to train deep neural networks (DNNs), but second-order methods are scarcely used because of the overpriced computing cost in getting the high-order information. In this paper, we propose the Damped Newton Stochastic Gradient Descent(DN-SGD) method and Stochastic Gradient Descent Damped Newton(SGD-DN) method to train DNNs for regression problems with Mean Square Error(MSE) and classification problems with Cross-Entropy Loss(CEL), which is inspired by a proved fact that the hessian matrix of last layer of DNNs is always semi-definite. Different from other second-order methods to estimate the hessian matrix of all parameters, our methods just accurately compute a small part of the parameters, which greatly reduces the computational cost and makes convergence of the learning process much faster and more accurate than SGD. Several numerical experiments on real datesets are performed to verify the effectiveness of our methods for regression and classification problems.