Provably Accurate and Scalable Linear Classifiers in Hyperbolic Spaces

Many high-dimensional practical data sets have hierarchical structures induced by graphs or time series. Such data sets are hard to process in Euclidean spaces and one often seeks low-dimensional embeddings in other space forms to perform the required learning tasks. For hierarchical data, the space of choice is a hyperbolic space because it guarantees low-distortion embeddings for tree-like structures. The geometry of hyperbolic spaces has properties not encountered in Euclidean spaces that pose challenges when trying to rigorously analyze algorithmic solutions. We propose a unified framework for learning scalable and simple hyperbolic linear classifiers with provable performance guarantees. The gist of our approach is to focus on Poincar\'e ball models and formulate the classification problems using tangent space formalisms. Our results include a new hyperbolic perceptron algorithm as well as an efficient and highly accurate convex optimization setup for hyperbolic support vector machine classifiers. Furthermore, we adapt our approach to accommodate second-order perceptrons, where data is preprocessed based on second-order information (correlation) to accelerate convergence, and strategic perceptrons, where potentially manipulated data arrives in an online manner and decisions are made sequentially. The excellent performance of the Poincar\'e second-order and strategic perceptrons shows that the proposed framework can be extended to general machine learning problems in hyperbolic spaces. Our experimental results, pertaining to synthetic, single-cell RNA-seq expression measurements, CIFAR10, Fashion-MNIST and mini-ImageNet, establish that all algorithms provably converge and have complexity comparable to those of their Euclidean counterparts. Accompanying codes can be found at: https://github.com/thupchnsky/PoincareLinearClassification.

You are AllSet: A Multiset Function Framework for Hypergraph Neural Networks

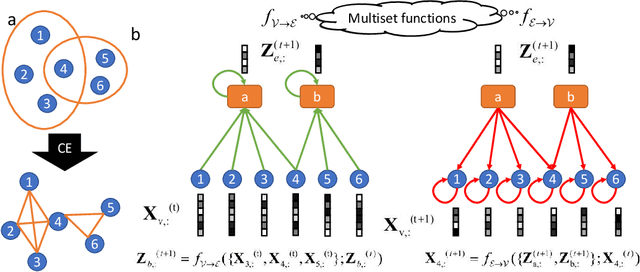
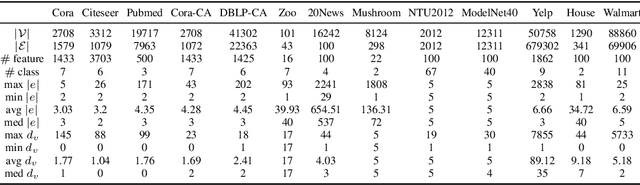
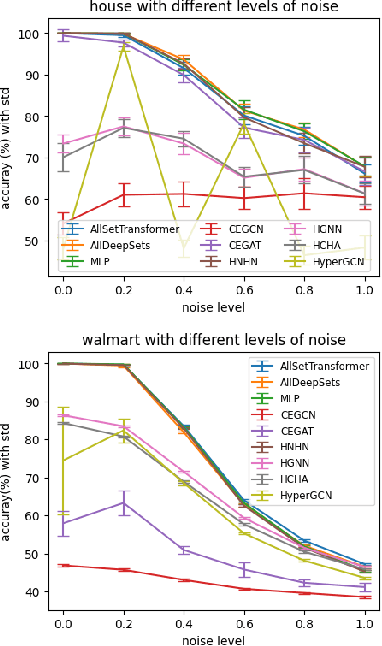
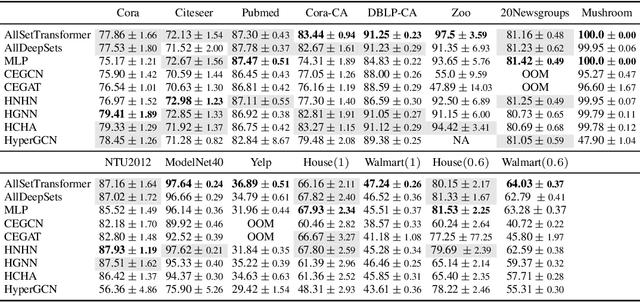
Hypergraphs are used to model higher-order interactions amongst agents and there exist many practically relevant instances of hypergraph datasets. To enable efficient processing of hypergraph-structured data, several hypergraph neural network platforms have been proposed for learning hypergraph properties and structure, with a special focus on node classification. However, almost all existing methods use heuristic propagation rules and offer suboptimal performance on many datasets. We propose AllSet, a new hypergraph neural network paradigm that represents a highly general framework for (hyper)graph neural networks and for the first time implements hypergraph neural network layers as compositions of two multiset functions that can be efficiently learned for each task and each dataset. Furthermore, AllSet draws on new connections between hypergraph neural networks and recent advances in deep learning of multiset functions. In particular, the proposed architecture utilizes Deep Sets and Set Transformer architectures that allow for significant modeling flexibility and offer high expressive power. To evaluate the performance of AllSet, we conduct the most extensive experiments to date involving ten known benchmarking datasets and three newly curated datasets that represent significant challenges for hypergraph node classification. The results demonstrate that AllSet has the unique ability to consistently either match or outperform all other hypergraph neural networks across the tested datasets. Our implementation and dataset will be released upon acceptance.

Joint Adaptive Feature Smoothing and Topology Extraction via Generalized PageRank GNNs

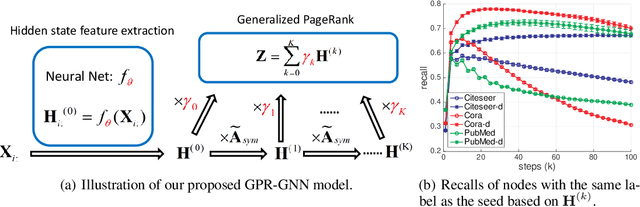
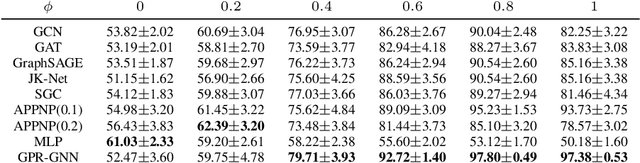
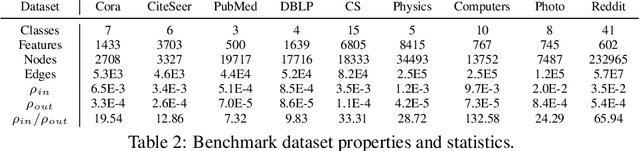
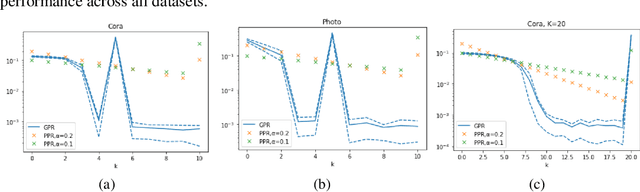
In many important applications, the acquired graph-structured data includes both node features and graph topology information. Graph neural networks (GNNs) are able to accurately process both the feature signals and graph topology individually. Nevertheless, they face the problem of trading-off the benefits of a shallow network architecture and deep multi-step information propagation when attempting to optimize their learning performance using both data components. Most existing GNN implementations based on node feature propagation are shallow due to the fact that a large number of propagation steps leads to feature over-smoothing and hence diminishes their discriminative power. In contrast, when processing topological information, it is common to use label propagation and PageRank methods that require a large number of message passing steps. We address these two contradictory requirements by combining GNNs with an adaptive generalized PageRank (GPR) scheme in a model termed GPR-GNN. GPR-GNN is the first known architecture that not only provably mitigates feature over-smoothing but also adaptively learns the weights of the GPR model to optimize topological information extraction. Our theoretical analysis of the GPR-GNN method is facilitated by novel synthetic benchmark datasets generated by the contextual stochastic block model. We also compare the performance of our NN architecture with that of several state-of-the-art GNNs on the problem of node-classification, using nine well-known benchmark datasets. The results demonstrate that GPR-GNN offers significant performance improvement compared to existing techniques on both synthetic and benchmark data.

Multi-MotifGAN (MMGAN): Motif-targeted Graph Generation and Prediction

Generative graph models create instances of graphs that mimic the properties of real-world networks. Generative models are successful at retaining pairwise associations in the underlying networks but often fail to capture higher-order connectivity patterns known as network motifs. Different types of graphs contain different network motifs, an example of which are triangles that often arise in social and biological networks. It is hence vital to capture these higher-order structures to simulate real-world networks accurately. We propose Multi-MotifGAN (MMGAN), a motif-targeted Generative Adversarial Network (GAN) that generalizes the benchmark NetGAN approach. The generalization consists of combining multiple biased random walks, each of which captures a different motif structure. MMGAN outperforms NetGAN at creating new graphs that accurately reflect the network motif statistics of input graphs such as Citeseer, Cora and Facebook.

Online Convex Dictionary Learning

Dictionary learning is a dimensionality reduction technique widely used in data mining, machine learning and signal processing alike. Nevertheless, many dictionary learning algorithms such as variants of Matrix Factorization (MF) do not adequately scale with the size of available datasets. Furthermore, scalable dictionary learning methods lack interpretability of the derived dictionary matrix. To mitigate these two issues, we propose a novel low-complexity, batch online convex dictionary learning algorithm. The algorithm sequentially processes small batches of data maintained in a fixed amount of storage space, and produces meaningful dictionaries that satisfy convexity constraints. Our analytical results are two-fold. First, we establish convergence guarantees for the proposed online learning scheme. Second, we show that a subsequence of the generated dictionaries converges to a stationary point of the approximation-error function. Experimental results on synthetic and real world datasets demonstrate both the computational savings of the proposed online method with respect to convex non-negative MF, and performance guarantees comparable to those of online non-convex learning.