Generalized Optimal Classification Trees: A Mixed-Integer Programming Approach

Global optimization of decision trees is a long-standing challenge in combinatorial optimization, yet such models play an important role in interpretable machine learning. Although the problem has been investigated for several decades, only recent advances in discrete optimization have enabled practical algorithms for solving optimal classification tree problems on real-world datasets. Mixed-integer programming (MIP) offers a high degree of modeling flexibility, and we therefore propose a MIP-based framework for learning optimal classification trees under nonlinear performance metrics, such as the F1-score, that explicitly addresses class imbalance. To improve scalability, we develop problem-specific acceleration techniques, including a tailored branch-and-cut algorithm, an instance-reduction scheme, and warm-start strategies. We evaluate the proposed approach on 50 benchmark datasets. The computational results show that the framework can efficiently optimize nonlinear metrics while achieving strong predictive performance and reduced solution times compared with existing methods.

HiBench: Benchmarking LLMs Capability on Hierarchical Structure Reasoning

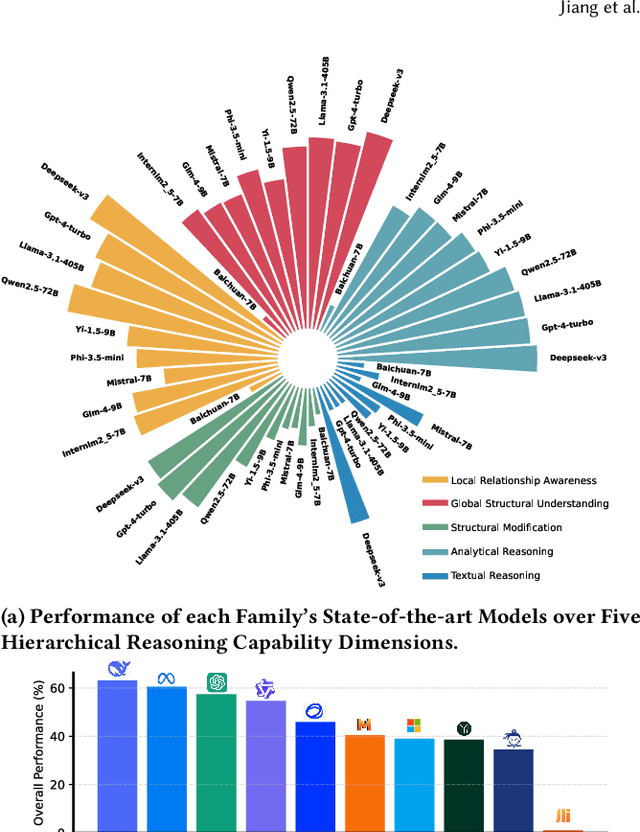
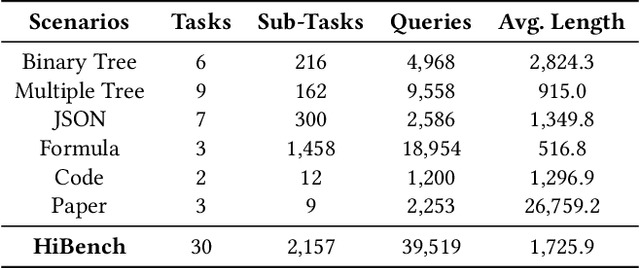
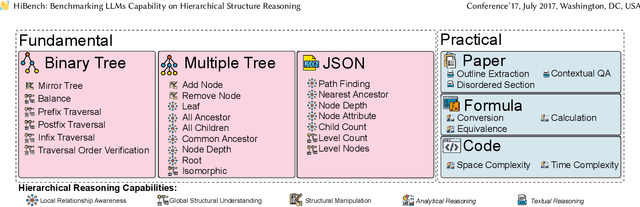
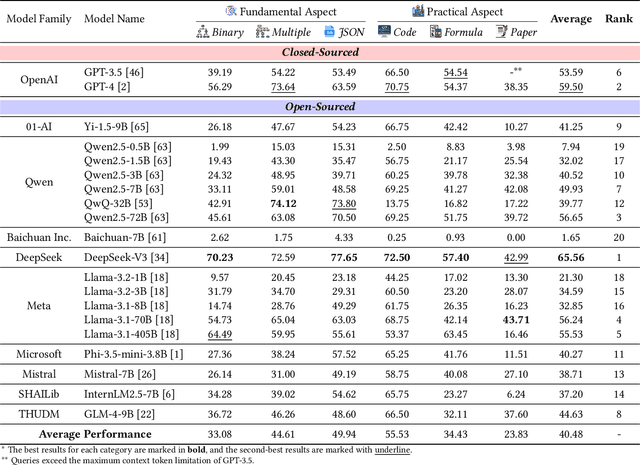
Structure reasoning is a fundamental capability of large language models (LLMs), enabling them to reason about structured commonsense and answer multi-hop questions. However, existing benchmarks for structure reasoning mainly focus on horizontal and coordinate structures (\emph{e.g.} graphs), overlooking the hierarchical relationships within them. Hierarchical structure reasoning is crucial for human cognition, particularly in memory organization and problem-solving. It also plays a key role in various real-world tasks, such as information extraction and decision-making. To address this gap, we propose HiBench, the first framework spanning from initial structure generation to final proficiency assessment, designed to benchmark the hierarchical reasoning capabilities of LLMs systematically. HiBench encompasses six representative scenarios, covering both fundamental and practical aspects, and consists of 30 tasks with varying hierarchical complexity, totaling 39,519 queries. To evaluate LLMs comprehensively, we develop five capability dimensions that depict different facets of hierarchical structure understanding. Through extensive evaluation of 20 LLMs from 10 model families, we reveal key insights into their capabilities and limitations: 1) existing LLMs show proficiency in basic hierarchical reasoning tasks; 2) they still struggle with more complex structures and implicit hierarchical representations, especially in structural modification and textual reasoning. Based on these findings, we create a small yet well-designed instruction dataset, which enhances LLMs' performance on HiBench by an average of 88.84\% (Llama-3.1-8B) and 31.38\% (Qwen2.5-7B) across all tasks. The HiBench dataset and toolkit are available here, https://github.com/jzzzzh/HiBench, to encourage evaluation.

BooleanOCT: Optimal Classification Trees based on multivariate Boolean Rules

The global optimization of classification trees has demonstrated considerable promise, notably in enhancing accuracy, optimizing size, and thereby improving human comprehensibility. While existing optimal classification trees substantially enhance accuracy over greedy-based tree models like CART, they still fall short when compared to the more complex black-box models, such as random forests. To bridge this gap, we introduce a new mixed-integer programming (MIP) formulation, grounded in multivariate Boolean rules, to derive the optimal classification tree. Our methodology integrates both linear metrics, including accuracy, balanced accuracy, and cost-sensitive cost, as well as nonlinear metrics such as the F1-score. The approach is implemented in an open-source Python package named BooleanOCT. We comprehensively benchmark these methods on the 36 datasets from the UCI machine learning repository. The proposed models demonstrate practical solvability on real-world datasets, effectively handling sizes in the tens of thousands. Aiming to maximize accuracy, this model achieves an average absolute improvement of 3.1\% and 1.5\% over random forests in small-scale and medium-sized datasets, respectively. Experiments targeting various objectives, including balanced accuracy, cost-sensitive cost, and F1-score, demonstrate the framework's wide applicability and its superiority over contemporary state-of-the-art optimal classification tree methods in small to medium-scale datasets.