Don't Forget to Connect! Improving RAG with Graph-based Reranking

Retrieval Augmented Generation (RAG) has greatly improved the performance of Large Language Model (LLM) responses by grounding generation with context from existing documents. These systems work well when documents are clearly relevant to a question context. But what about when a document has partial information, or less obvious connections to the context? And how should we reason about connections between documents? In this work, we seek to answer these two core questions about RAG generation. We introduce G-RAG, a reranker based on graph neural networks (GNNs) between the retriever and reader in RAG. Our method combines both connections between documents and semantic information (via Abstract Meaning Representation graphs) to provide a context-informed ranker for RAG. G-RAG outperforms state-of-the-art approaches while having smaller computational footprint. Additionally, we assess the performance of PaLM 2 as a reranker and find it to significantly underperform G-RAG. This result emphasizes the importance of reranking for RAG even when using Large Language Models.

Does Sparsity Help in Learning Misspecified Linear Bandits?

Recently, the study of linear misspecified bandits has generated intriguing implications of the hardness of learning in bandits and reinforcement learning (RL). In particular, Du et al. (2020) show that even if a learner is given linear features in $\mathbb{R}^d$ that approximate the rewards in a bandit or RL with a uniform error of $\varepsilon$, searching for an $O(\varepsilon)$-optimal action requires pulling at least $\Omega(\exp(d))$ queries. Furthermore, Lattimore et al. (2020) show that a degraded $O(\varepsilon\sqrt{d})$-optimal solution can be learned within $\operatorname{poly}(d/\varepsilon)$ queries. Yet it is unknown whether a structural assumption on the ground-truth parameter, such as sparsity, could break the $\varepsilon\sqrt{d}$ barrier. In this paper, we address this question by showing that algorithms can obtain $O(\varepsilon)$-optimal actions by querying $O(\varepsilon^{-s}d^s)$ actions, where $s$ is the sparsity parameter, removing the $\exp(d)$-dependence. We then establish information-theoretical lower bounds, i.e., $\Omega(\exp(s))$, to show that our upper bound on sample complexity is nearly tight if one demands an error $ O(s^{\delta}\varepsilon)$ for $0<\delta<1$. For $\delta\geq 1$, we further show that $\operatorname{poly}(s/\varepsilon)$ queries are possible when the linear features are "good" and even in general settings. These results provide a nearly complete picture of how sparsity can help in misspecified bandit learning and provide a deeper understanding of when linear features are "useful" for bandit and reinforcement learning with misspecification.

Global Neighbor Sampling for Mixed CPU-GPU Training on Giant Graphs

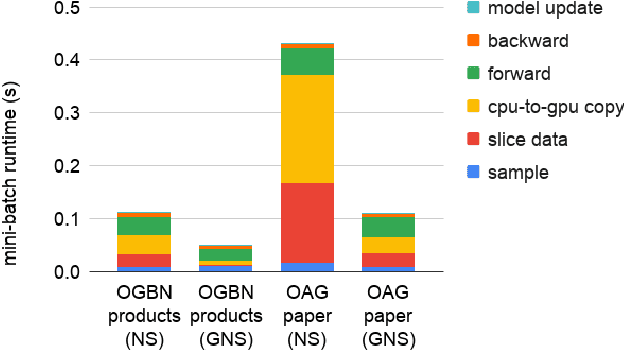
Graph neural networks (GNNs) are powerful tools for learning from graph data and are widely used in various applications such as social network recommendation, fraud detection, and graph search. The graphs in these applications are typically large, usually containing hundreds of millions of nodes. Training GNN models on such large graphs efficiently remains a big challenge. Despite a number of sampling-based methods have been proposed to enable mini-batch training on large graphs, these methods have not been proved to work on truly industry-scale graphs, which require GPUs or mixed-CPU-GPU training. The state-of-the-art sampling-based methods are usually not optimized for these real-world hardware setups, in which data movement between CPUs and GPUs is a bottleneck. To address this issue, we propose Global Neighborhood Sampling that aims at training GNNs on giant graphs specifically for mixed-CPU-GPU training. The algorithm samples a global cache of nodes periodically for all mini-batches and stores them in GPUs. This global cache allows in-GPU importance sampling of mini-batches, which drastically reduces the number of nodes in a mini-batch, especially in the input layer, to reduce data copy between CPU and GPU and mini-batch computation without compromising the training convergence rate or model accuracy. We provide a highly efficient implementation of this method and show that our implementation outperforms an efficient node-wise neighbor sampling baseline by a factor of 2X-4X on giant graphs. It outperforms an efficient implementation of LADIES with small layers by a factor of 2X-14X while achieving much higher accuracy than LADIES.We also theoretically analyze the proposed algorithm and show that with cached node data of a proper size, it enjoys a comparable convergence rate as the underlying node-wise sampling method.

Faster Activity and Data Detection in Massive Random Access: A Multi-armed Bandit Approach

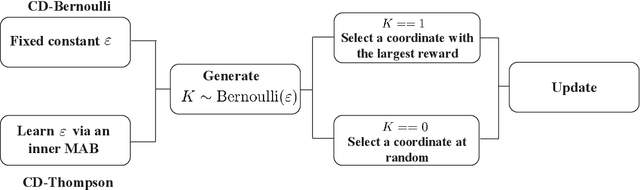
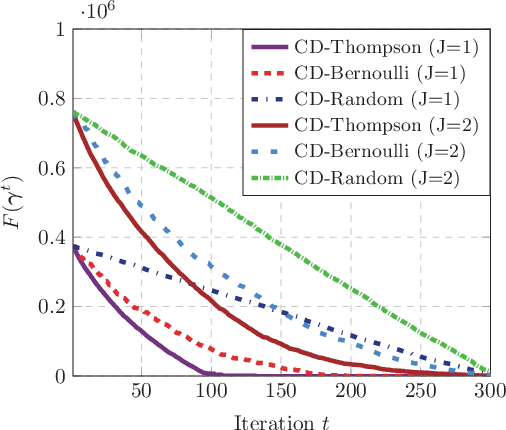
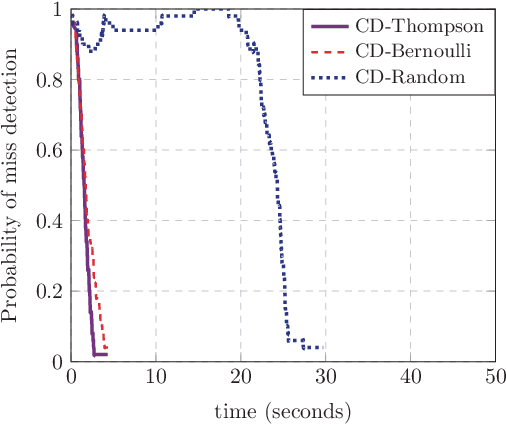
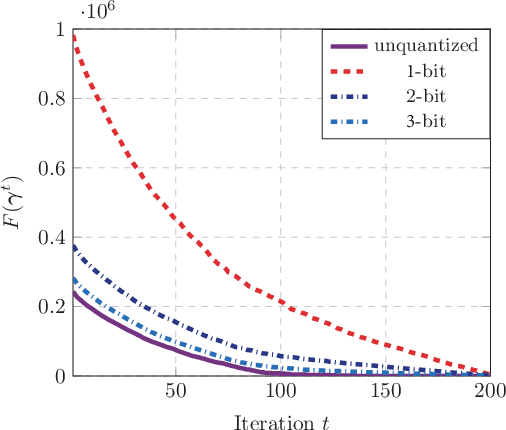
This paper investigates the grant-free random access with massive IoT devices. By embedding the data symbols in the signature sequences, joint device activity detection and data decoding can be achieved, which, however, significantly increases the computational complexity. Coordinate descent algorithms that enjoy a low per-iteration complexity have been employed to solve the detection problem, but previous works typically employ a random coordinate selection policy which leads to slow convergence. In this paper, we develop multi-armed bandit approaches for more efficient detection via coordinate descent, which make a delicate trade-off between exploration and exploitation in coordinate selection. Specifically, we first propose a bandit based strategy, i.e., Bernoulli sampling, to speed up the convergence rate of coordinate descent, by learning which coordinates will result in more aggressive descent of the objective function. To further improve the convergence rate, an inner multi-armed bandit problem is established to learn the exploration policy of Bernoulli sampling. Both convergence rate analysis and simulation results are provided to show that the proposed bandit based algorithms enjoy faster convergence rates with a lower time complexity compared with the state-of-the-art algorithm. Furthermore, our proposed algorithms are applicable to different scenarios, e.g., massive random access with low-precision analog-to-digital converters (ADCs).

Blind Over-the-Air Computation and Data Fusion via Provable Wirtinger Flow

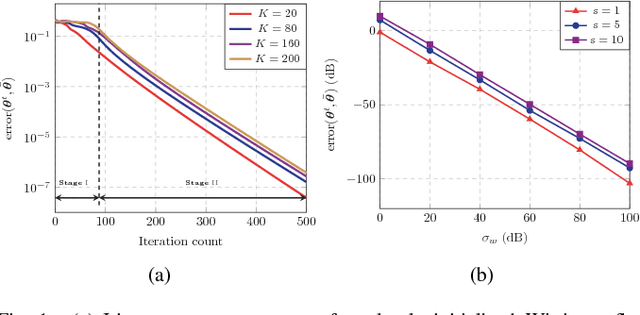
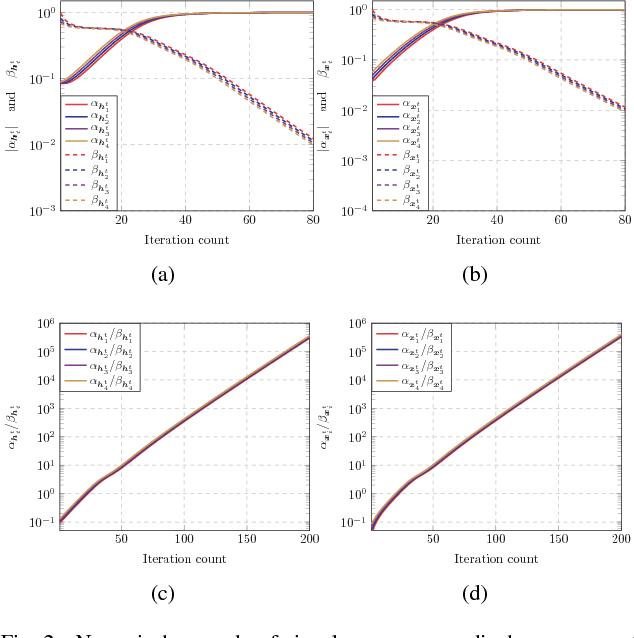
Over-the-air computation (AirComp) shows great promise to support fast data fusion in Internet-of-Things (IoT) networks. AirComp typically computes desired functions of distributed sensing data by exploiting superposed data transmission in multiple access channels. To overcome its reliance on channel station information (CSI), this work proposes a novel blind over-the-air computation (BlairComp) without requiring CSI access, particularly for low complexity and low latency IoT networks. To solve the resulting non-convex optimization problem without the initialization dependency exhibited by the solutions of a number of recently proposed efficient algorithms, we develop a Wirtinger flow solution to the BlairComp problem based on random initialization. To analyze the resulting efficiency, we prove its statistical optimality and global convergence guarantee. Specifically, in the first stage of the algorithm, the iteration of randomly initialized Wirtinger flow given sufficient data samples can enter a local region that enjoys strong convexity and strong smoothness within a few iterations. We also prove the estimation error of BlairComp in the local region to be sufficiently small. We show that, at the second stage of the algorithm, its estimation error decays exponentially at a linear convergence rate.

Nonconvex Demixing From Bilinear Measurements

We consider the problem of demixing a sequence of source signals from the sum of noisy bilinear measurements. It is a generalized mathematical model for blind demixing with blind deconvolution, which is prevalent across the areas of dictionary learning, image processing, and communications. However, state-of- the-art convex methods for blind demixing via semidefinite programming are computationally infeasible for large-scale problems. Although the existing nonconvex algorithms are able to address the scaling issue, they normally require proper regularization to establish optimality guarantees. The additional regularization yields tedious algorithmic parameters and pessimistic convergence rates with conservative step sizes. To address the limitations of existing methods, we thus develop a provable nonconvex demixing procedure viaWirtinger flow, much like vanilla gradient descent, to harness the benefits of regularization-free fast convergence rate with aggressive step size and computational optimality guarantees. This is achieved by exploiting the benign geometry of the blind demixing problem, thereby revealing that Wirtinger flow enforces the regularization-free iterates in the region of strong convexity and qualified level of smoothness, where the step size can be chosen aggressively.