Faster Activity and Data Detection in Massive Random Access: A Multi-armed Bandit Approach
Paper and Code
Jan 28, 2020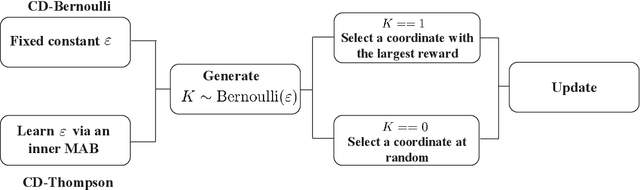
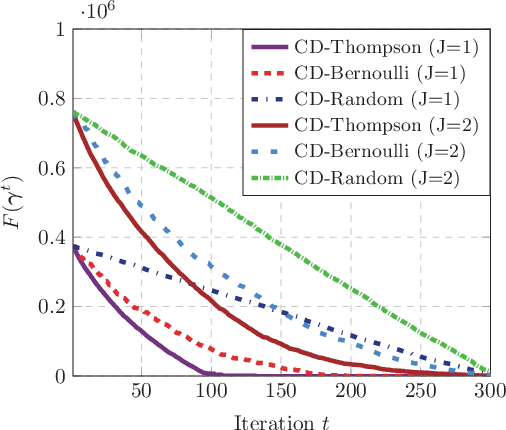
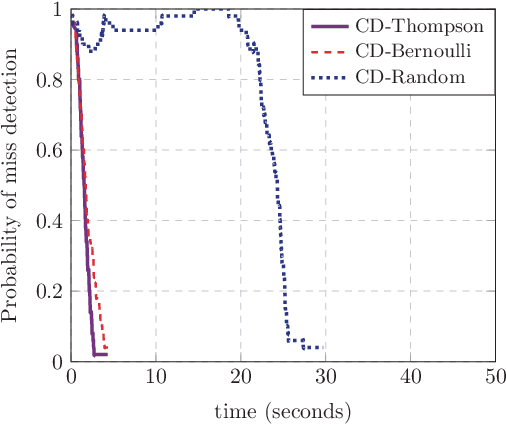
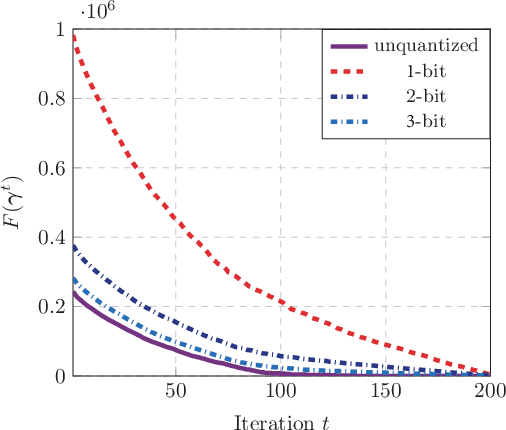
This paper investigates the grant-free random access with massive IoT devices. By embedding the data symbols in the signature sequences, joint device activity detection and data decoding can be achieved, which, however, significantly increases the computational complexity. Coordinate descent algorithms that enjoy a low per-iteration complexity have been employed to solve the detection problem, but previous works typically employ a random coordinate selection policy which leads to slow convergence. In this paper, we develop multi-armed bandit approaches for more efficient detection via coordinate descent, which make a delicate trade-off between exploration and exploitation in coordinate selection. Specifically, we first propose a bandit based strategy, i.e., Bernoulli sampling, to speed up the convergence rate of coordinate descent, by learning which coordinates will result in more aggressive descent of the objective function. To further improve the convergence rate, an inner multi-armed bandit problem is established to learn the exploration policy of Bernoulli sampling. Both convergence rate analysis and simulation results are provided to show that the proposed bandit based algorithms enjoy faster convergence rates with a lower time complexity compared with the state-of-the-art algorithm. Furthermore, our proposed algorithms are applicable to different scenarios, e.g., massive random access with low-precision analog-to-digital converters (ADCs).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge