Toward Next-Generation Artificial Intelligence: Catalyzing the NeuroAI Revolution

Neuroscience has long been an important driver of progress in artificial intelligence (AI). We propose that to accelerate progress in AI, we must invest in fundamental research in NeuroAI.

How do neurons operate on sparse distributed representations? A mathematical theory of sparsity, neurons and active dendrites

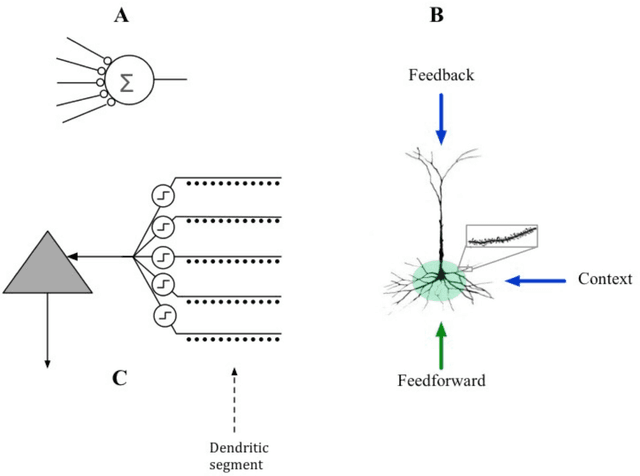
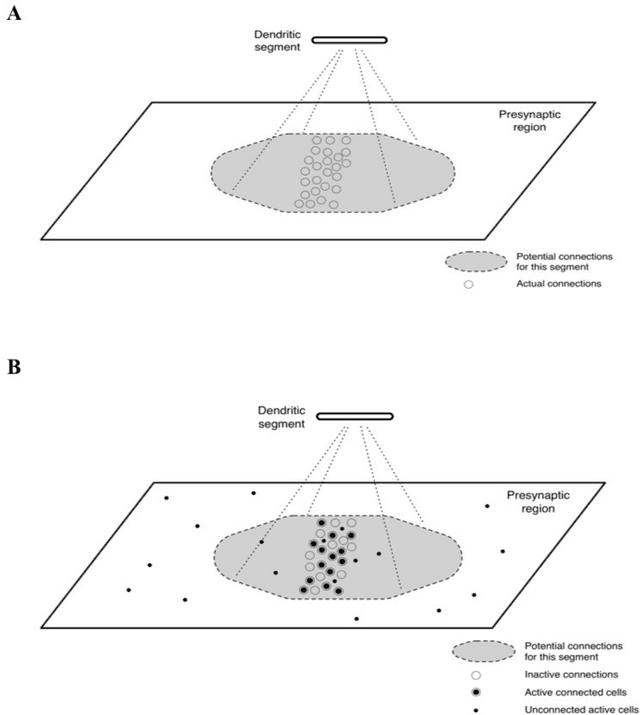
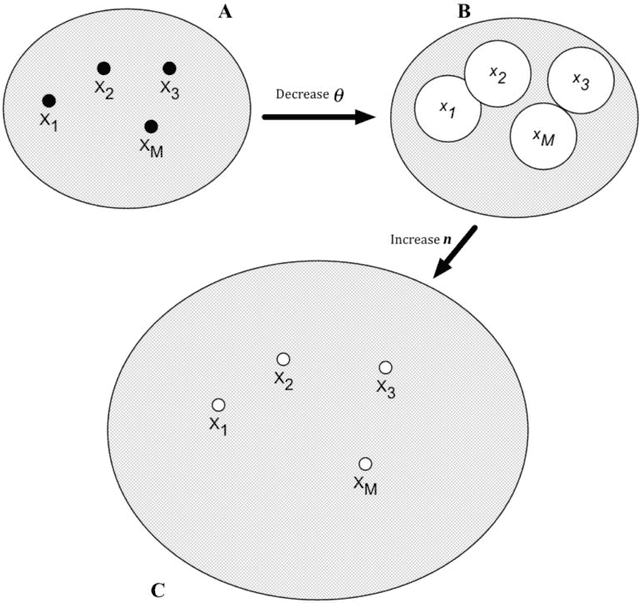
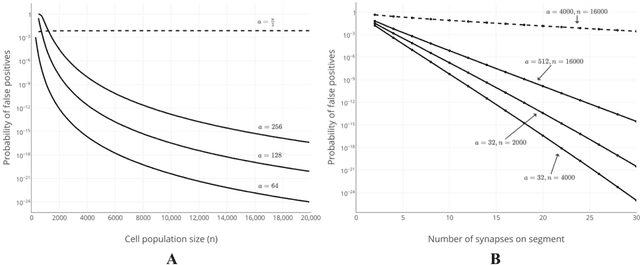
We propose a formal mathematical model for sparse representations and active dendrites in neocortex. Our model is inspired by recent experimental findings on active dendritic processing and NMDA spikes in pyramidal neurons. These experimental and modeling studies suggest that the basic unit of pattern memory in the neocortex is instantiated by small clusters of synapses operated on by localized non-linear dendritic processes. We derive a number of scaling laws that characterize the accuracy of such dendrites in detecting activation patterns in a neuronal population under adverse conditions. We introduce the union property which shows that synapses for multiple patterns can be randomly mixed together within a segment and still lead to highly accurate recognition. We describe simulation results that provide further insight into sparse representations as well as two primary results. First we show that pattern recognition by a neuron with active dendrites can be extremely accurate and robust with high dimensional sparse inputs even when using a tiny number of synapses to recognize large patterns. Second, equations representing recognition accuracy of a dendrite predict optimal NMDA spiking thresholds under a generous set of assumptions. The prediction tightly matches NMDA spiking thresholds measured in the literature. Our model matches many of the known properties of pyramidal neurons. As such the theory provides a mathematical framework for understanding the benefits and limits of sparse representations in cortical networks.

Continuous online sequence learning with an unsupervised neural network model

The ability to recognize and predict temporal sequences of sensory inputs is vital for survival in natural environments. Based on many known properties of cortical neurons, hierarchical temporal memory (HTM) sequence memory is recently proposed as a theoretical framework for sequence learning in the cortex. In this paper, we analyze properties of HTM sequence memory and apply it to sequence learning and prediction problems with streaming data. We show the model is able to continuously learn a large number of variable-order temporal sequences using an unsupervised Hebbian-like learning rule. The sparse temporal codes formed by the model can robustly handle branching temporal sequences by maintaining multiple predictions until there is sufficient disambiguating evidence. We compare the HTM sequence memory with other sequence learning algorithms, including statistical methods: autoregressive integrated moving average (ARIMA), feedforward neural networks: online sequential extreme learning machine (ELM), and recurrent neural networks: long short-term memory (LSTM) and echo-state networks (ESN), on sequence prediction problems with both artificial and real-world data. The HTM model achieves comparable accuracy to other state-of-the-art algorithms. The model also exhibits properties that are critical for sequence learning, including continuous online learning, the ability to handle multiple predictions and branching sequences with high order statistics, robustness to sensor noise and fault tolerance, and good performance without task-specific hyper- parameters tuning. Therefore the HTM sequence memory not only advances our understanding of how the brain may solve the sequence learning problem, but is also applicable to a wide range of real-world problems such as discrete and continuous sequence prediction, anomaly detection, and sequence classification.

Why Neurons Have Thousands of Synapses, A Theory of Sequence Memory in Neocortex

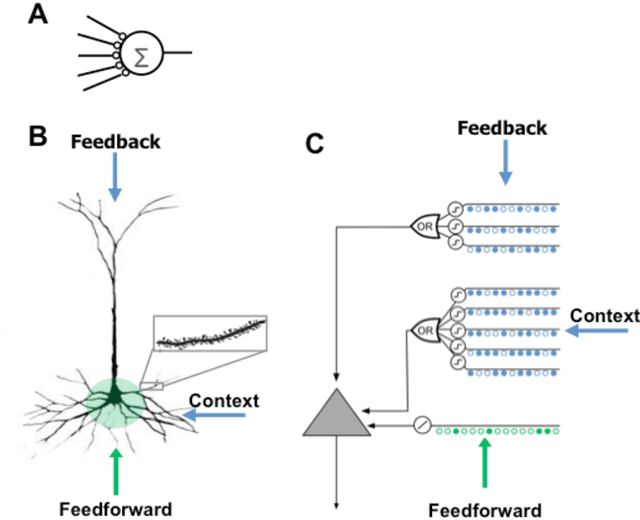
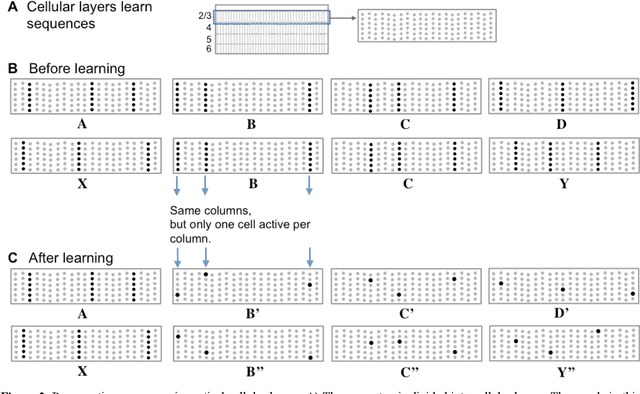
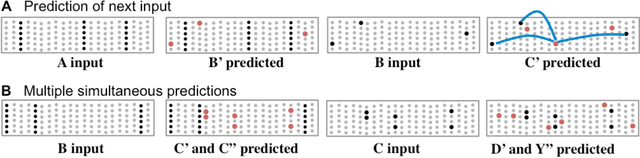
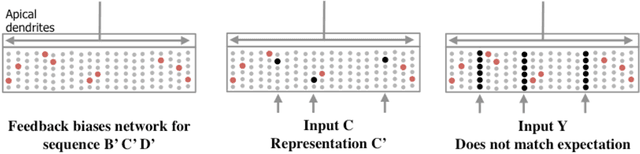
Neocortical neurons have thousands of excitatory synapses. It is a mystery how neurons integrate the input from so many synapses and what kind of large-scale network behavior this enables. It has been previously proposed that non-linear properties of dendrites enable neurons to recognize multiple patterns. In this paper we extend this idea by showing that a neuron with several thousand synapses arranged along active dendrites can learn to accurately and robustly recognize hundreds of unique patterns of cellular activity, even in the presence of large amounts of noise and pattern variation. We then propose a neuron model where some of the patterns recognized by a neuron lead to action potentials and define the classic receptive field of the neuron, whereas the majority of the patterns recognized by a neuron act as predictions by slightly depolarizing the neuron without immediately generating an action potential. We then present a network model based on neurons with these properties and show that the network learns a robust model of time-based sequences. Given the similarity of excitatory neurons throughout the neocortex and the importance of sequence memory in inference and behavior, we propose that this form of sequence memory is a universal property of neocortical tissue. We further propose that cellular layers in the neocortex implement variations of the same sequence memory algorithm to achieve different aspects of inference and behavior. The neuron and network models we introduce are robust over a wide range of parameters as long as the network uses a sparse distributed code of cellular activations. The sequence capacity of the network scales linearly with the number of synapses on each neuron. Thus neurons need thousands of synapses to learn the many temporal patterns in sensory stimuli and motor sequences.

Properties of Sparse Distributed Representations and their Application to Hierarchical Temporal Memory

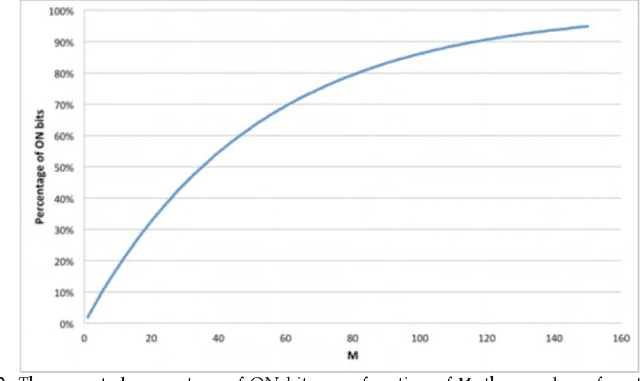
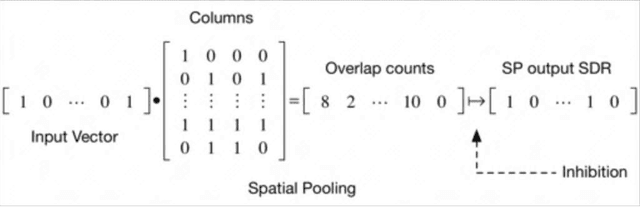
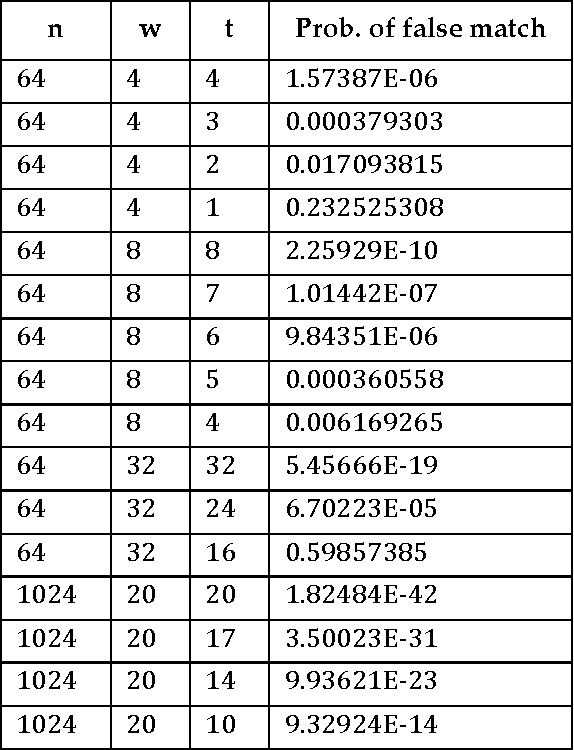
Empirical evidence demonstrates that every region of the neocortex represents information using sparse activity patterns. This paper examines Sparse Distributed Representations (SDRs), the primary information representation strategy in Hierarchical Temporal Memory (HTM) systems and the neocortex. We derive a number of properties that are core to scaling, robustness, and generalization. We use the theory to provide practical guidelines and illustrate the power of SDRs as the basis of HTM. Our goal is to help create a unified mathematical and practical framework for SDRs as it relates to cortical function.