Efficiency Separation between RL Methods: Model-Free, Model-Based and Goal-Conditioned

We prove a fundamental limitation on the efficiency of a wide class of Reinforcement Learning (RL) algorithms. This limitation applies to model-free RL methods as well as a broad range of model-based methods, such as planning with tree search. Under an abstract definition of this class, we provide a family of RL problems for which these methods suffer a lower bound exponential in the horizon for their interactions with the environment to find an optimal behavior. However, there exists a method, not tailored to this specific family of problems, which can efficiently solve the problems in the family. In contrast, our limitation does not apply to several types of methods proposed in the literature, for instance, goal-conditioned methods or other algorithms that construct an inverse dynamics model.

A model-based approach to meta-Reinforcement Learning: Transformers and tree search

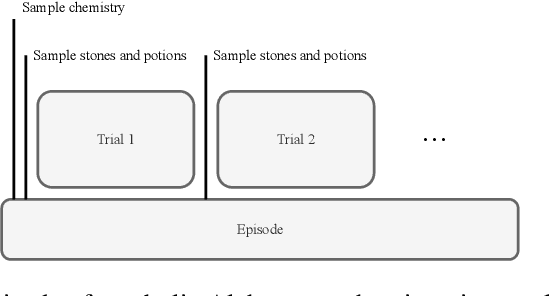
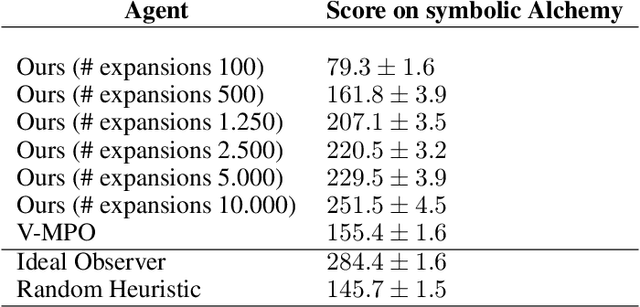
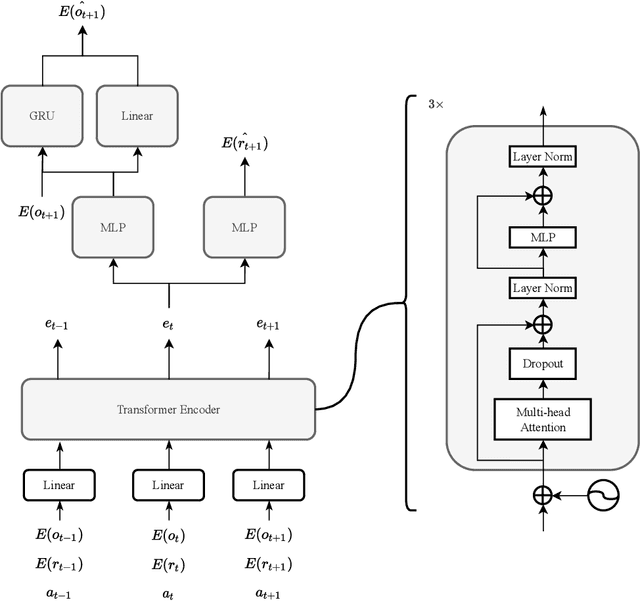
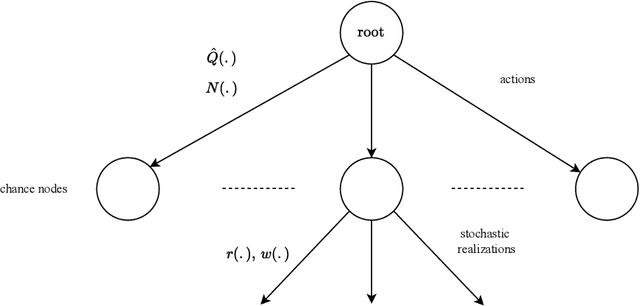
Meta-learning is a line of research that develops the ability to leverage past experiences to efficiently solve new learning problems. Meta-Reinforcement Learning (meta-RL) methods demonstrate a capability to learn behaviors that efficiently acquire and exploit information in several meta-RL problems. In this context, the Alchemy benchmark has been proposed by Wang et al. [2021]. Alchemy features a rich structured latent space that is challenging for state-of-the-art model-free RL methods. These methods fail to learn to properly explore then exploit. We develop a model-based algorithm. We train a model whose principal block is a Transformer Encoder to fit the symbolic Alchemy environment dynamics. Then we define an online planner with the learned model using a tree search method. This algorithm significantly outperforms previously applied model-free RL methods on the symbolic Alchemy problem. Our results reveal the relevance of model-based approaches with online planning to perform exploration and exploitation successfully in meta-RL. Moreover, we show the efficiency of the Transformer architecture to learn complex dynamics that arise from latent spaces present in meta-RL problems.

PAC-learning gains of Turing machines over circuits and neural networks

A caveat to many applications of the current Deep Learning approach is the need for large-scale data. One improvement suggested by Kolmogorov Complexity results is to apply the minimum description length principle with computationally universal models. We study the potential gains in sample efficiency that this approach can bring in principle. We use polynomial-time Turing machines to represent computationally universal models and Boolean circuits to represent Artificial Neural Networks (ANNs) acting on finite-precision digits. Our analysis unravels direct links between our question and Computational Complexity results. We provide lower and upper bounds on the potential gains in sample efficiency between the MDL applied with Turing machines instead of ANNs. Our bounds depend on the bit-size of the input of the Boolean function to be learned. Furthermore, we highlight close relationships between classical open problems in Circuit Complexity and the tightness of these.

Unsupervised Network Embedding for Graph Visualization, Clustering and Classification

A main challenge in mining network-based data is finding effective ways to represent or encode graph structures so that it can be efficiently exploited by machine learning algorithms. Several methods have focused in network representation at node/edge or substructure level. However, many real life challenges such as time-varying, multilayer, chemical compounds and brain networks involve analysis of a family of graphs instead of single one opening additional challenges in graph comparison and representation. Traditional approaches for learning representations relies on hand-crafting specialized heuristics to extract meaningful information about the graphs, e.g statistical properties, structural features, etc. as well as engineered graph distances to quantify dissimilarity between networks. In this work we provide an unsupervised approach to learn embedding representation for a collection of graphs so that it can be used in numerous graph mining tasks. By using an unsupervised neural network approach on input graphs, we aim to capture the underlying distribution of the data in order to discriminate between different class of networks. Our method is assessed empirically on synthetic and real life datasets and evaluated in three different tasks: graph clustering, visualization and classification. Results reveal that our method outperforms well known graph distances and graph-kernels in clustering and classification tasks, being highly efficient in runtime.

Multi-hop assortativities for networks classification

Several social, medical, engineering and biological challenges rely on discovering the functionality of networks from their structure and node metadata, when is available. For example, in chemoinformatics one might want to detect whether a molecule is toxic based on structure and atomic types, or discover the research field for scientific collaboration networks. Existing techniques rely on counting or measuring structural patterns that are known to show large variations from network to network, such as number of triangles, or the assortativity of node metadata. We introduce the concept of multi-hop assortativity, that captures the similarity of node situated at the extremities of a randomly selected path of a given length. We show that multi-hop assortativity unifies various existing concepts and offers a versatile family of fingerprints to characterize networks. These fingerprints allow in turn to recover the functionalities of a network, with the help of the machine learning toolbox. Our method is evaluated empirically on established social and chemoinformatic network benchmarks. Results reveal that our assortativity based features are competitive providing highly accurate results often outperforming state of the art methods for the network classification task

Positive semi-definite embedding for dimensionality reduction and out-of-sample extensions

In machine learning or statistics, it is often desirable to reduce the dimensionality of high dimensional data. We propose to obtain the low dimensional embedding coordinates as the eigenvectors of a positive semi-definite kernel matrix. This kernel matrix is the solution of a semi-definite program promoting a low rank solution and defined with the help of a diffusion kernel. Besides, we also discuss an infinite dimensional analogue of the same semi-definite program. From a practical perspective, a main feature of our approach is the existence of a non-linear out-of-sample extension formula of the embedding coordinates that we call a projected Nystr\"om approximation. This extension formula yields an extension of the kernel matrix to a data-dependent Mercer kernel function. Although the semi-definite program may be solved directly, we propose another strategy based on a rank constrained formulation solved thanks to a projected power method algorithm followed by a singular value decomposition. This strategy allows for a reduced computational time.

Dynamics Based Features For Graph Classification

Numerous social, medical, engineering and biological challenges can be framed as graph-based learning tasks. Here, we propose a new feature based approach to network classification. We show how dynamics on a network can be useful to reveal patterns about the organization of the components of the underlying graph where the process takes place. We define generalized assortativities on networks and use them as generalized features across multiple time scales. These features turn out to be suitable signatures for discriminating between different classes of networks. Our method is evaluated empirically on established network benchmarks. We also introduce a new dataset of human brain networks (connectomes) and use it to evaluate our method. Results reveal that our dynamics based features are competitive and often outperform state of the art accuracies.