Efficiency Separation between RL Methods: Model-Free, Model-Based and Goal-Conditioned

We prove a fundamental limitation on the efficiency of a wide class of Reinforcement Learning (RL) algorithms. This limitation applies to model-free RL methods as well as a broad range of model-based methods, such as planning with tree search. Under an abstract definition of this class, we provide a family of RL problems for which these methods suffer a lower bound exponential in the horizon for their interactions with the environment to find an optimal behavior. However, there exists a method, not tailored to this specific family of problems, which can efficiently solve the problems in the family. In contrast, our limitation does not apply to several types of methods proposed in the literature, for instance, goal-conditioned methods or other algorithms that construct an inverse dynamics model.

A model-based approach to meta-Reinforcement Learning: Transformers and tree search

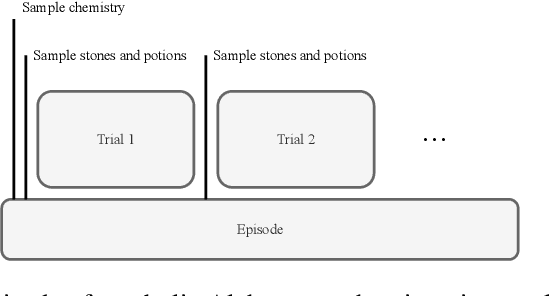
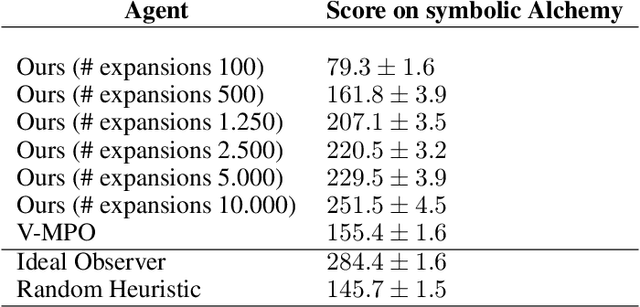
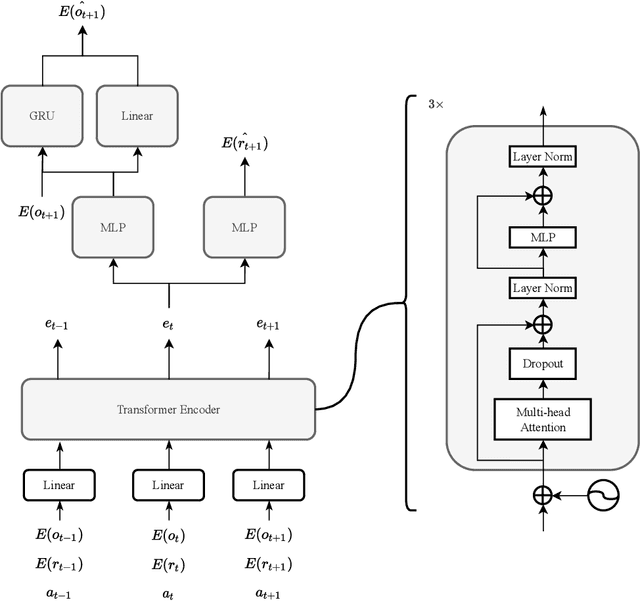
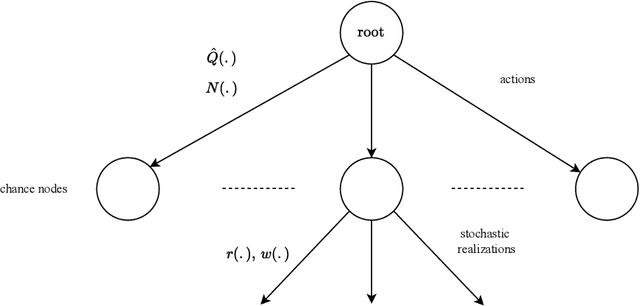
Meta-learning is a line of research that develops the ability to leverage past experiences to efficiently solve new learning problems. Meta-Reinforcement Learning (meta-RL) methods demonstrate a capability to learn behaviors that efficiently acquire and exploit information in several meta-RL problems. In this context, the Alchemy benchmark has been proposed by Wang et al. [2021]. Alchemy features a rich structured latent space that is challenging for state-of-the-art model-free RL methods. These methods fail to learn to properly explore then exploit. We develop a model-based algorithm. We train a model whose principal block is a Transformer Encoder to fit the symbolic Alchemy environment dynamics. Then we define an online planner with the learned model using a tree search method. This algorithm significantly outperforms previously applied model-free RL methods on the symbolic Alchemy problem. Our results reveal the relevance of model-based approaches with online planning to perform exploration and exploitation successfully in meta-RL. Moreover, we show the efficiency of the Transformer architecture to learn complex dynamics that arise from latent spaces present in meta-RL problems.

PAC-learning gains of Turing machines over circuits and neural networks

A caveat to many applications of the current Deep Learning approach is the need for large-scale data. One improvement suggested by Kolmogorov Complexity results is to apply the minimum description length principle with computationally universal models. We study the potential gains in sample efficiency that this approach can bring in principle. We use polynomial-time Turing machines to represent computationally universal models and Boolean circuits to represent Artificial Neural Networks (ANNs) acting on finite-precision digits. Our analysis unravels direct links between our question and Computational Complexity results. We provide lower and upper bounds on the potential gains in sample efficiency between the MDL applied with Turing machines instead of ANNs. Our bounds depend on the bit-size of the input of the Boolean function to be learned. Furthermore, we highlight close relationships between classical open problems in Circuit Complexity and the tightness of these.

A linear bound on the k-rendezvous time for primitive sets of NZ matrices

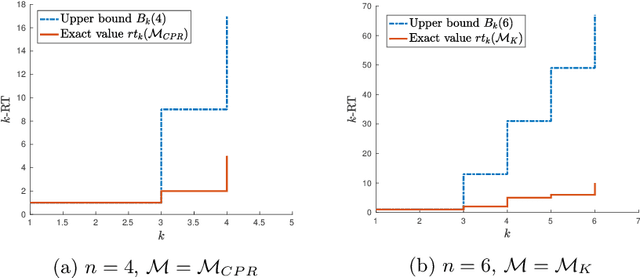
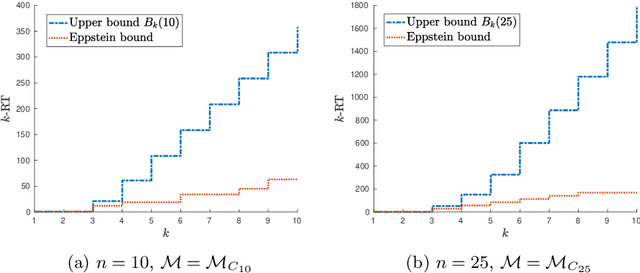
A set of nonnegative matrices is called primitive if there exists a product of these matrices that is entrywise positive. Motivated by recent results relating synchronizing automata and primitive sets, we study the length of the shortest product of a primitive set having a column or a row with k positive entries (the k-RT). We prove that this value is at most linear w.r.t. the matrix size n for small k, while the problem is still open for synchronizing automata. We then report numerical results comparing our upper bound on the k-RT with heuristic approximation methods.