Privacy-Preserving Synthetically Augmented Knowledge Graphs with Semantic Utility

Knowledge Graphs (KGs) have recently gained relevant attention in many application domains, from healthcare to biotechnology, from logistics to finance. Financial organisations, central banks, economic research entities, and national supervision authorities apply ontological reasoning on KGs to address crucial business tasks, such as economic policymaking, banking supervision, anti-money laundering, and economic research. Reasoning allows for the generation of derived knowledge capturing complex business semantics and the set up of effective business processes. A major obstacle in KGs sharing is represented by privacy considerations since the identity of the data subjects and their sensitive or company-confidential information may be improperly exposed. In this paper, we propose a novel framework to enable KGs sharing while ensuring that information that should remain private is not directly released nor indirectly exposed via derived knowledge, while maintaining the embedded knowledge of the KGs to support business downstream tasks. Our approach produces a privacy-preserving synthetic KG as an augmentation of the input one via the introduction of structural anonymisation. We introduce a novel privacy measure for KGs, which considers derived knowledge and a new utility metric that captures the business semantics we want to preserve, and propose two novel anonymization algorithms. Our extensive experimental evaluation, with both synthetic graphs and real-world datasets, confirms the effectiveness of our approach achieving up to a 70% improvement in the privacy of entities compared to existing methods not specifically designed for KGs.

A linear bound on the k-rendezvous time for primitive sets of NZ matrices

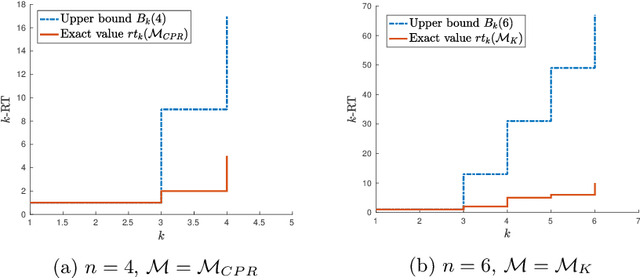
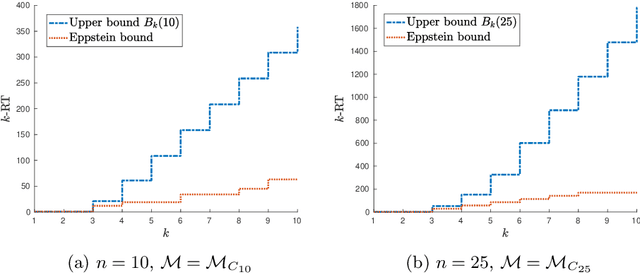
A set of nonnegative matrices is called primitive if there exists a product of these matrices that is entrywise positive. Motivated by recent results relating synchronizing automata and primitive sets, we study the length of the shortest product of a primitive set having a column or a row with k positive entries (the k-RT). We prove that this value is at most linear w.r.t. the matrix size n for small k, while the problem is still open for synchronizing automata. We then report numerical results comparing our upper bound on the k-RT with heuristic approximation methods.