Know Your Model : Increasing Trust in AI and Machine Learning

The widespread utilization of AI systems has drawn attention to the potential impacts of such systems on society. Of particular concern are the consequences that prediction errors may have on real-world scenarios, and the trust humanity places in AI systems. It is necessary to understand how we can evaluate trustworthiness in AI and how individuals and entities alike can develop trustworthy AI systems. In this paper, we analyze each element of trustworthiness and provide a set of 20 guidelines that can be leveraged to ensure optimal AI functionality while taking into account the greater ethical, technical, and practical impacts to humanity. Moreover, the guidelines help ensure that trustworthiness is provable and can be demonstrated, they are implementation agnostic, and they can be applied to any AI system in any sector.

VecHGrad for solving accurately complex tensor decomposition

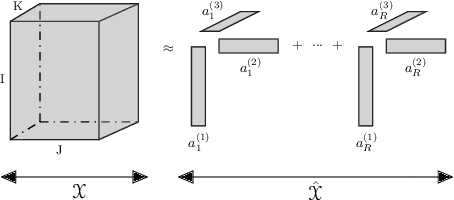
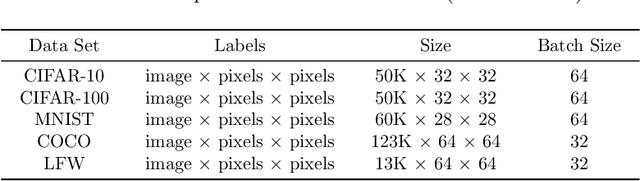
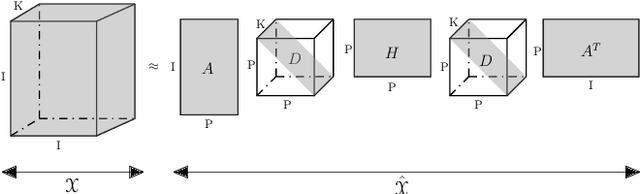
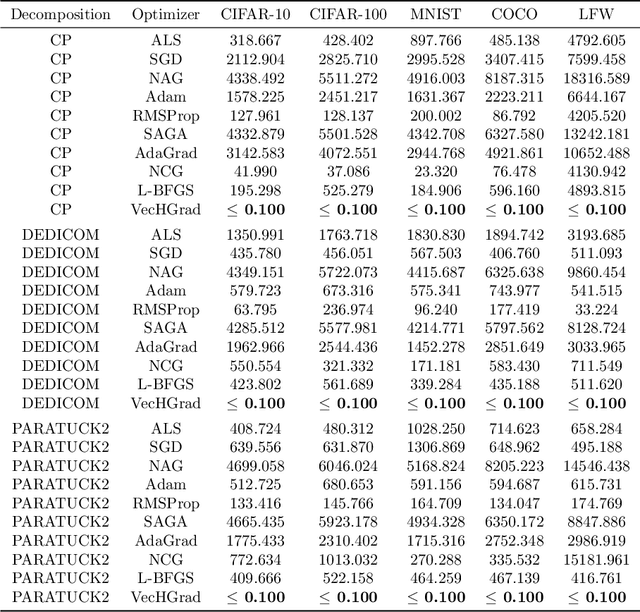
Tensor decomposition, a collection of factorization techniques for multidimensional arrays, are among the most general and powerful tools for scientific analysis. However, because of their increasing size, today's data sets require more complex tensor decomposition involving factorization with multiple matrices and diagonal tensors such as DEDICOM or PARATUCK2. Traditional tensor resolution algorithms such as Stochastic Gradient Descent (SGD), Non-linear Conjugate Gradient descent (NCG) or Alternating Least Square (ALS), cannot be easily applied to complex tensor decomposition or often lead to poor accuracy at convergence. We propose a new resolution algorithm, called VecHGrad, for accurate and efficient stochastic resolution over all existing tensor decomposition, specifically designed for complex decomposition. VecHGrad relies on gradient, Hessian-vector product and adaptive line search to ensure the convergence during optimization. Our experiments on five real-world data sets with the state-of-the-art deep learning gradient optimization models show that VecHGrad is capable of converging considerably faster because of its superior theoretical convergence rate per step. Therefore, VecHGrad targets as well deep learning optimizer algorithms. The experiments are performed for various tensor decomposition including CP, DEDICOM and PARATUCK2. Although it involves a slightly more complex update rule, VecHGrad's runtime is similar in practice to that of gradient methods such as SGD, Adam or RMSProp.

MQLV: Modified Q-Learning for Vasicek Model

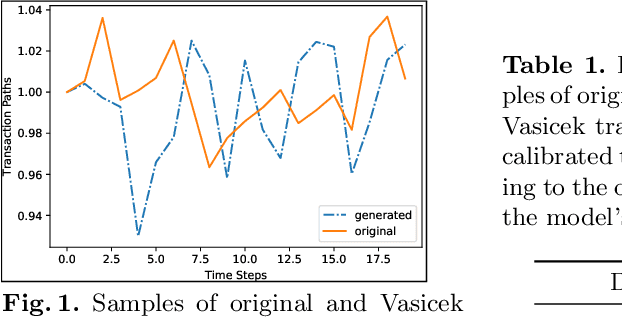
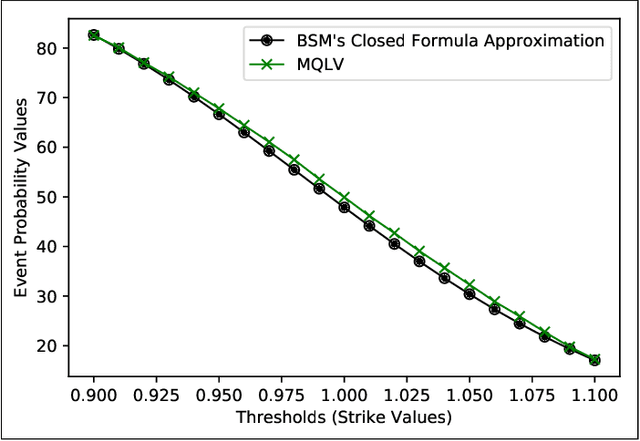
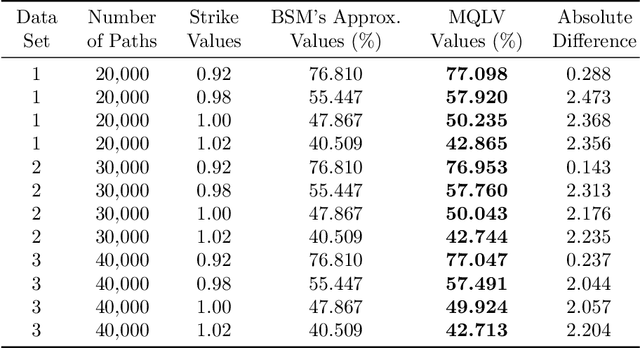
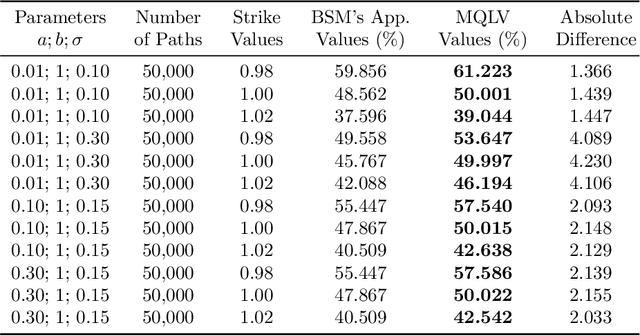
In a reinforcement learning approach, an optimal value function is learned across a set of actions, or decisions, that leads to a set of states giving different rewards, with the objective to maximize the overall reward. A policy assigns to each state-action pairs an expected return. We call an optimal policy a policy for which the value function is optimal. QLBS, Q-Learner in the Black-Scholes(-Merton) Worlds, applies the reinforcement learning concepts, and noticeably, the popular Q-learning algorithm, to the financial stochastic model described by Black, Scholes and Merton. However, QLBS is specifically optimized for the geometric Brownian motion and the pricing of vanilla options. Consequently, it suffers from the traditional over-estimation of the Q-values reflected by an over-estimation of the vanilla option prices. Furthermore, its range of application is limited to vanilla option pricing within the financial markets. We propose MQLV, Modified Q-Learner for the Vasicek model, a new reinforcement learning approach that limits the Q-values over-estimation observed in QLBS and extends the simulation to mean reverting stochastic diffusion processes. Additionally, MQLV uses a digital function to estimate the future probability of an event, thus widening the scope of the financial application to any other domain involving time series. Our experiments underline the potential of MQLV on generated Monte Carlo simulations, particularly representative of the retail banking time series. In particular, MQLV is able to determine the optimal policy of money management based on the aggregated financial transactions of the clients, unlocking new frontiers to establish personalized credit card limits or loans. Finally, MQLV is the first methodology compatible with the Vasicek model capable of an event probability estimation targeting simulation of event probabilities in retail banking.

PHom-WAE: Persitent Homology for Wasserstein Auto-Encoders

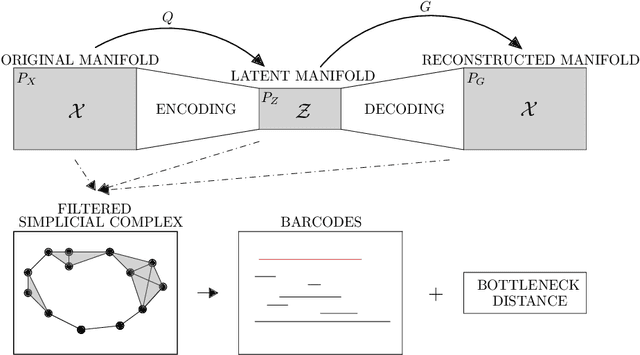
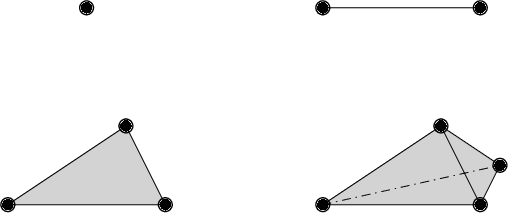
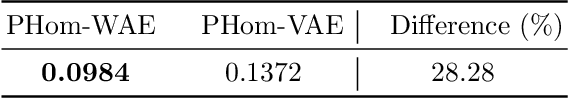
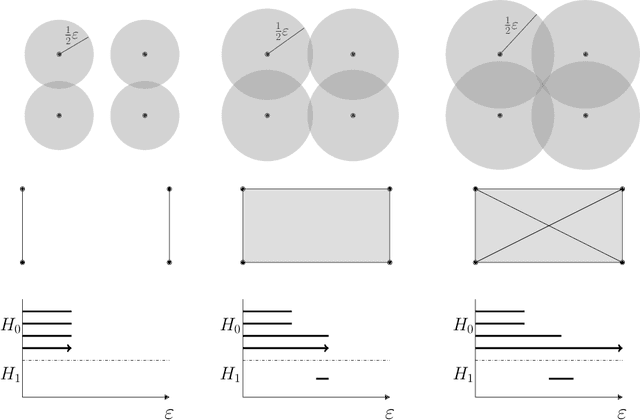
Auto-encoders are among the most popular neural network architecture for dimension reduction. They are composed of two parts: the encoder which maps the model distribution to a latent manifold and the decoder which maps the latent manifold to a reconstructed distribution. However, auto-encoders are known to provoke chaotically scattered data distribution in the latent manifold resulting in an incomplete reconstructed distribution. Current distance measures fail to detect this problem because they are not able to acknowledge the shape of the data manifolds, i.e. their topological features, and the scale at which the manifolds should be analyzed. We propose Persistent Homology for Wasserstein Auto-Encoders, called PHom-WAE, a new methodology to assess and measure the data distribution of a generative model. PHom-WAE minimizes the Wasserstein distance between the true distribution and the reconstructed distribution and uses persistent homology, the study of the topological features of a space at different spatial resolutions, to compare the nature of the latent manifold and the reconstructed distribution. Our experiments underline the potential of persistent homology for Wasserstein Auto-Encoders in comparison to Variational Auto-Encoders, another type of generative model. The experiments are conducted on a real-world data set particularly challenging for traditional distance measures and auto-encoders. PHom-WAE is the first methodology to propose a topological distance measure, the bottleneck distance, for Wasserstein Auto-Encoders used to compare decoded samples of high quality in the context of credit card transactions.

PHom-GeM: Persistent Homology for Generative Models

Generative neural network models, including Generative Adversarial Network (GAN) and Auto-Encoders (AE), are among the most popular neural network models to generate adversarial data. The GAN model is composed of a generator that produces synthetic data and of a discriminator that discriminates between the generator's output and the true data. AE consist of an encoder which maps the model distribution to a latent manifold and of a decoder which maps the latent manifold to a reconstructed distribution. However, generative models are known to provoke chaotically scattered reconstructed distribution during their training, and consequently, incomplete generated adversarial distributions. Current distance measures fail to address this problem because they are not able to acknowledge the shape of the data manifold, i.e. its topological features, and the scale at which the manifold should be analyzed. We propose Persistent Homology for Generative Models, PHom-GeM, a new methodology to assess and measure the distribution of a generative model. PHom-GeM minimizes an objective function between the true and the reconstructed distributions and uses persistent homology, the study of the topological features of a space at different spatial resolutions, to compare the nature of the true and the generated distributions. Our experiments underline the potential of persistent homology for Wasserstein GAN in comparison to Wasserstein AE and Variational AE. The experiments are conducted on a real-world data set particularly challenging for traditional distance measures and generative neural network models. PHom-GeM is the first methodology to propose a topological distance measure, the bottleneck distance, for generative models used to compare adversarial samples in the context of credit card transactions.

Predicting Sparse Clients' Actions with CPOPT-Net in the Banking Environment

The digital revolution of the banking system with evolving European regulations have pushed the major banking actors to innovate by a newly use of their clients' digital information. Given highly sparse client activities, we propose CPOPT-Net, an algorithm that combines the CP canonical tensor decomposition, a multidimensional matrix decomposition that factorizes a tensor as the sum of rank-one tensors, and neural networks. CPOPT-Net removes efficiently sparse information with a gradient-based resolution while relying on neural networks for time series predictions. Our experiments show that CPOPT-Net is capable to perform accurate predictions of the clients' actions in the context of personalized recommendation. CPOPT-Net is the first algorithm to use non-linear conjugate gradient tensor resolution with neural networks to propose predictions of financial activities on a public data set.

User-Device Authentication in Mobile Banking using APHEN for Paratuck2 Tensor Decomposition

The new financial European regulations such as PSD2 are changing the retail banking services. Noticeably, the monitoring of the personal expenses is now opened to other institutions than retail banks. Nonetheless, the retail banks are looking to leverage the user-device authentication on the mobile banking applications to enhance the personal financial advertisement. To address the profiling of the authentication, we rely on tensor decomposition, a higher dimensional analogue of matrix decomposition. We use Paratuck2, which expresses a tensor as a multiplication of matrices and diagonal tensors, because of the imbalance between the number of users and devices. We highlight why Paratuck2 is more appropriate in this case than the popular CP tensor decomposition, which decomposes a tensor as a sum of rank-one tensors. However, the computation of Paratuck2 is computational intensive. We propose a new APproximate HEssian-based Newton resolution algorithm, APHEN, capable of solving Paratuck2 more accurately and faster than the other popular approaches based on alternating least square or gradient descent. The results of Paratuck2 are used for the predictions of users' authentication with neural networks. We apply our method for the concrete case of targeting clients for financial advertising campaigns based on the authentication events generated by mobile banking applications.