MQLV: Modified Q-Learning for Vasicek Model

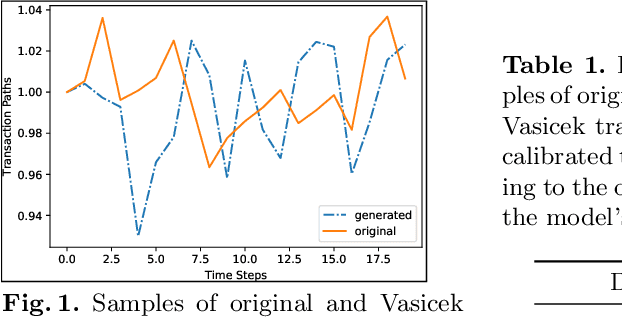
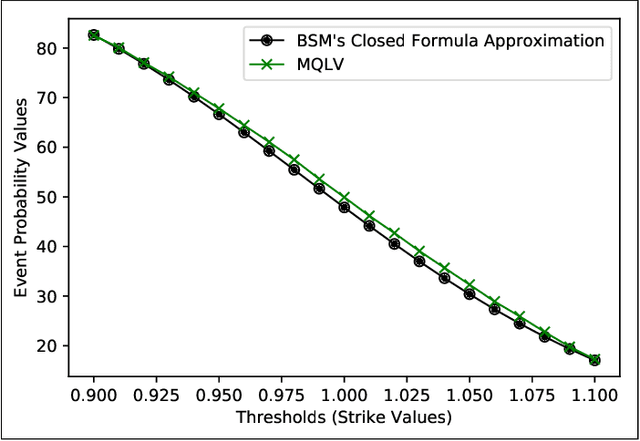
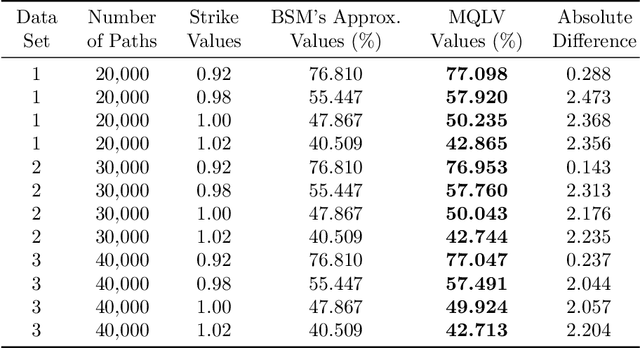
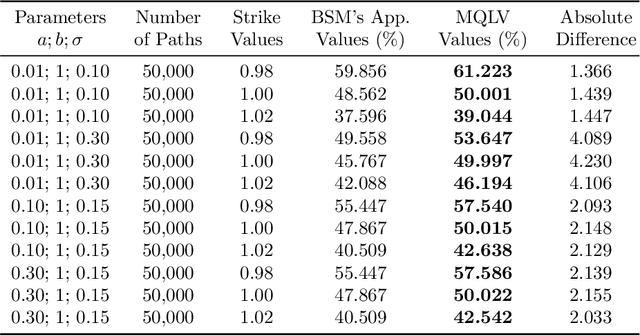
In a reinforcement learning approach, an optimal value function is learned across a set of actions, or decisions, that leads to a set of states giving different rewards, with the objective to maximize the overall reward. A policy assigns to each state-action pairs an expected return. We call an optimal policy a policy for which the value function is optimal. QLBS, Q-Learner in the Black-Scholes(-Merton) Worlds, applies the reinforcement learning concepts, and noticeably, the popular Q-learning algorithm, to the financial stochastic model described by Black, Scholes and Merton. However, QLBS is specifically optimized for the geometric Brownian motion and the pricing of vanilla options. Consequently, it suffers from the traditional over-estimation of the Q-values reflected by an over-estimation of the vanilla option prices. Furthermore, its range of application is limited to vanilla option pricing within the financial markets. We propose MQLV, Modified Q-Learner for the Vasicek model, a new reinforcement learning approach that limits the Q-values over-estimation observed in QLBS and extends the simulation to mean reverting stochastic diffusion processes. Additionally, MQLV uses a digital function to estimate the future probability of an event, thus widening the scope of the financial application to any other domain involving time series. Our experiments underline the potential of MQLV on generated Monte Carlo simulations, particularly representative of the retail banking time series. In particular, MQLV is able to determine the optimal policy of money management based on the aggregated financial transactions of the clients, unlocking new frontiers to establish personalized credit card limits or loans. Finally, MQLV is the first methodology compatible with the Vasicek model capable of an event probability estimation targeting simulation of event probabilities in retail banking.