SynGAN: Towards Generating Synthetic Network Attacks using GANs

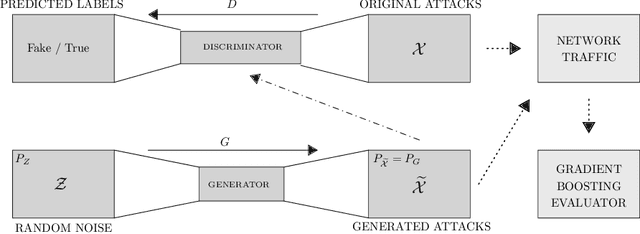
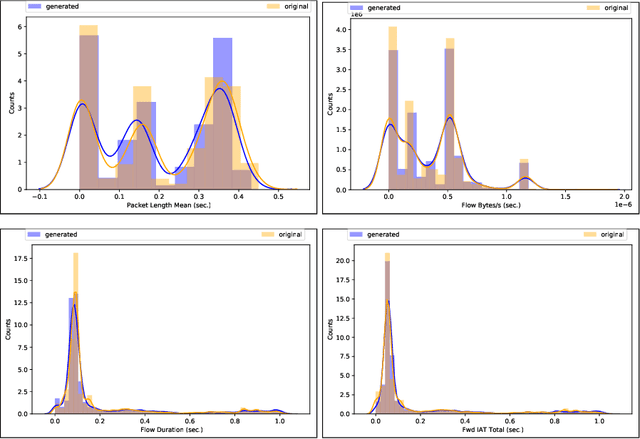
The rapid digital transformation without security considerations has resulted in the rise of global-scale cyberattacks. The first line of defense against these attacks are Network Intrusion Detection Systems (NIDS). Once deployed, however, these systems work as blackboxes with a high rate of false positives with no measurable effectiveness. There is a need to continuously test and improve these systems by emulating real-world network attack mutations. We present SynGAN, a framework that generates adversarial network attacks using the Generative Adversial Networks (GAN). SynGAN generates malicious packet flow mutations using real attack traffic, which can improve NIDS attack detection rates. As a first step, we compare two public datasets, NSL-KDD and CICIDS2017, for generating synthetic Distributed Denial of Service (DDoS) network attacks. We evaluate the attack quality (real vs. synthetic) using a gradient boosting classifier.

VecHGrad for solving accurately complex tensor decomposition

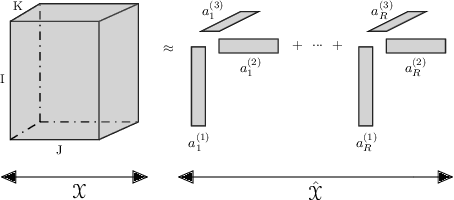
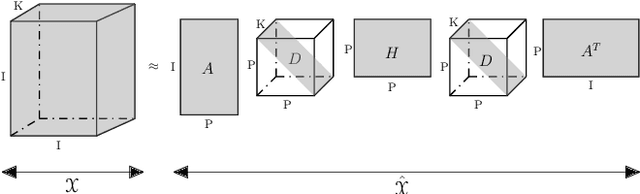
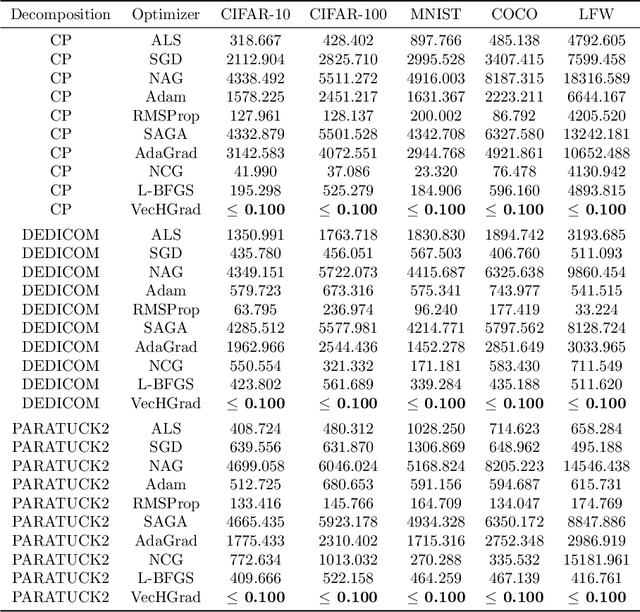
Tensor decomposition, a collection of factorization techniques for multidimensional arrays, are among the most general and powerful tools for scientific analysis. However, because of their increasing size, today's data sets require more complex tensor decomposition involving factorization with multiple matrices and diagonal tensors such as DEDICOM or PARATUCK2. Traditional tensor resolution algorithms such as Stochastic Gradient Descent (SGD), Non-linear Conjugate Gradient descent (NCG) or Alternating Least Square (ALS), cannot be easily applied to complex tensor decomposition or often lead to poor accuracy at convergence. We propose a new resolution algorithm, called VecHGrad, for accurate and efficient stochastic resolution over all existing tensor decomposition, specifically designed for complex decomposition. VecHGrad relies on gradient, Hessian-vector product and adaptive line search to ensure the convergence during optimization. Our experiments on five real-world data sets with the state-of-the-art deep learning gradient optimization models show that VecHGrad is capable of converging considerably faster because of its superior theoretical convergence rate per step. Therefore, VecHGrad targets as well deep learning optimizer algorithms. The experiments are performed for various tensor decomposition including CP, DEDICOM and PARATUCK2. Although it involves a slightly more complex update rule, VecHGrad's runtime is similar in practice to that of gradient methods such as SGD, Adam or RMSProp.

MQLV: Modified Q-Learning for Vasicek Model

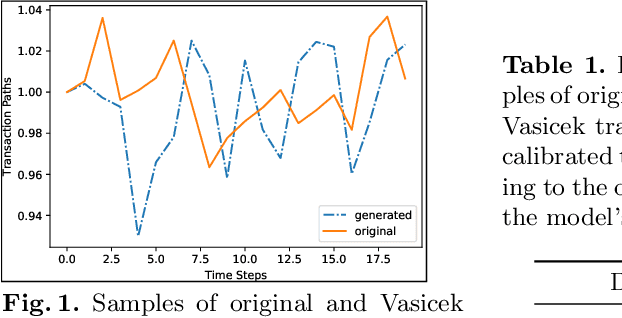
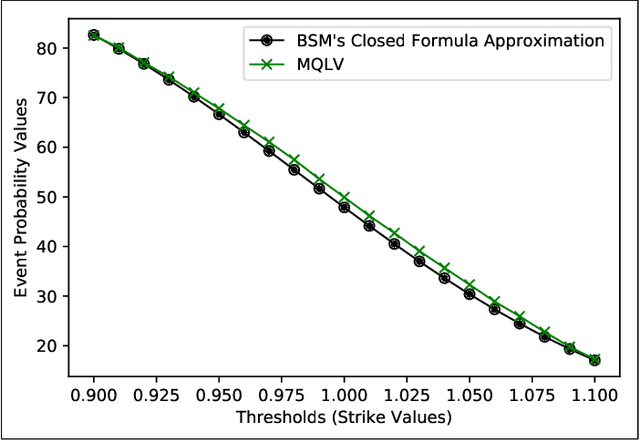
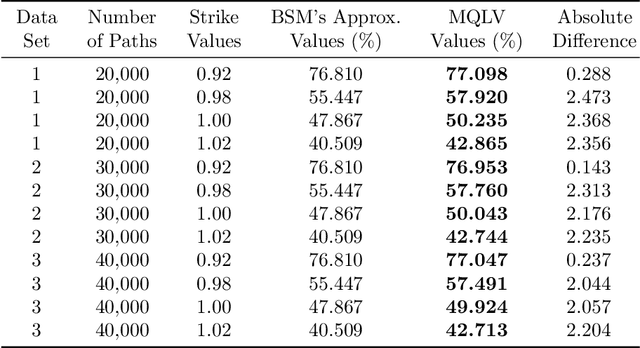
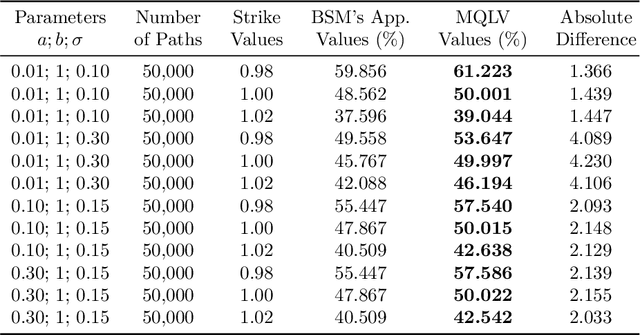
In a reinforcement learning approach, an optimal value function is learned across a set of actions, or decisions, that leads to a set of states giving different rewards, with the objective to maximize the overall reward. A policy assigns to each state-action pairs an expected return. We call an optimal policy a policy for which the value function is optimal. QLBS, Q-Learner in the Black-Scholes(-Merton) Worlds, applies the reinforcement learning concepts, and noticeably, the popular Q-learning algorithm, to the financial stochastic model described by Black, Scholes and Merton. However, QLBS is specifically optimized for the geometric Brownian motion and the pricing of vanilla options. Consequently, it suffers from the traditional over-estimation of the Q-values reflected by an over-estimation of the vanilla option prices. Furthermore, its range of application is limited to vanilla option pricing within the financial markets. We propose MQLV, Modified Q-Learner for the Vasicek model, a new reinforcement learning approach that limits the Q-values over-estimation observed in QLBS and extends the simulation to mean reverting stochastic diffusion processes. Additionally, MQLV uses a digital function to estimate the future probability of an event, thus widening the scope of the financial application to any other domain involving time series. Our experiments underline the potential of MQLV on generated Monte Carlo simulations, particularly representative of the retail banking time series. In particular, MQLV is able to determine the optimal policy of money management based on the aggregated financial transactions of the clients, unlocking new frontiers to establish personalized credit card limits or loans. Finally, MQLV is the first methodology compatible with the Vasicek model capable of an event probability estimation targeting simulation of event probabilities in retail banking.

PHom-WAE: Persitent Homology for Wasserstein Auto-Encoders

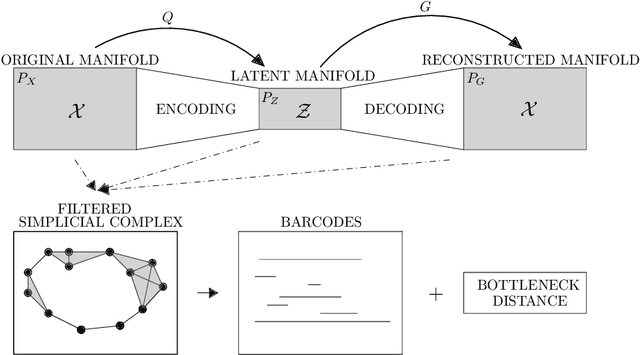
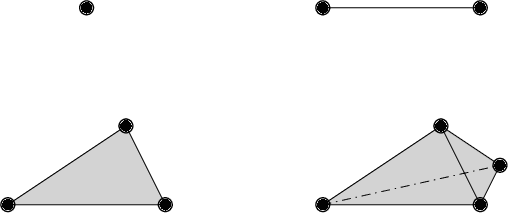
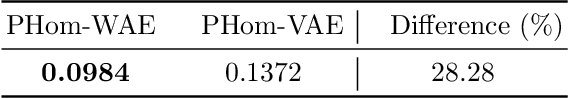
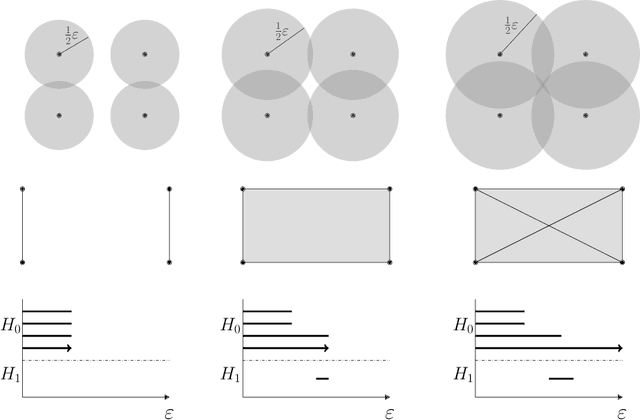
Auto-encoders are among the most popular neural network architecture for dimension reduction. They are composed of two parts: the encoder which maps the model distribution to a latent manifold and the decoder which maps the latent manifold to a reconstructed distribution. However, auto-encoders are known to provoke chaotically scattered data distribution in the latent manifold resulting in an incomplete reconstructed distribution. Current distance measures fail to detect this problem because they are not able to acknowledge the shape of the data manifolds, i.e. their topological features, and the scale at which the manifolds should be analyzed. We propose Persistent Homology for Wasserstein Auto-Encoders, called PHom-WAE, a new methodology to assess and measure the data distribution of a generative model. PHom-WAE minimizes the Wasserstein distance between the true distribution and the reconstructed distribution and uses persistent homology, the study of the topological features of a space at different spatial resolutions, to compare the nature of the latent manifold and the reconstructed distribution. Our experiments underline the potential of persistent homology for Wasserstein Auto-Encoders in comparison to Variational Auto-Encoders, another type of generative model. The experiments are conducted on a real-world data set particularly challenging for traditional distance measures and auto-encoders. PHom-WAE is the first methodology to propose a topological distance measure, the bottleneck distance, for Wasserstein Auto-Encoders used to compare decoded samples of high quality in the context of credit card transactions.