VecHGrad for solving accurately complex tensor decomposition

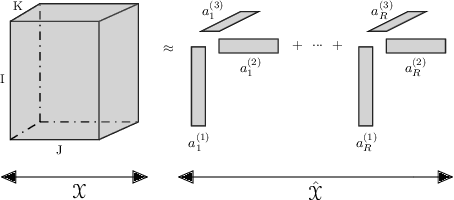
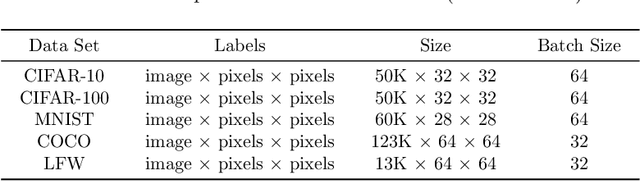
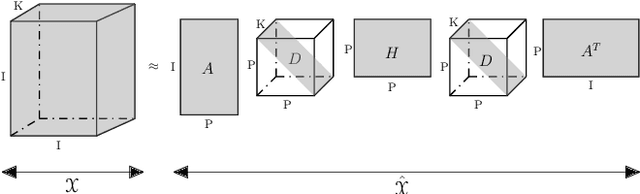
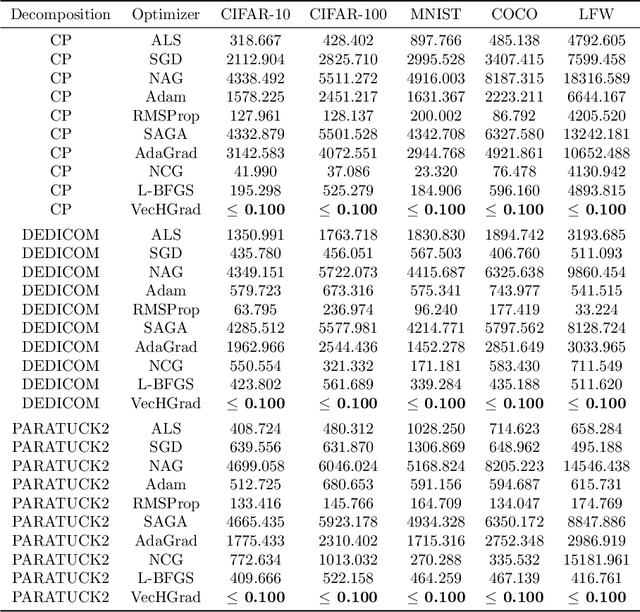
Tensor decomposition, a collection of factorization techniques for multidimensional arrays, are among the most general and powerful tools for scientific analysis. However, because of their increasing size, today's data sets require more complex tensor decomposition involving factorization with multiple matrices and diagonal tensors such as DEDICOM or PARATUCK2. Traditional tensor resolution algorithms such as Stochastic Gradient Descent (SGD), Non-linear Conjugate Gradient descent (NCG) or Alternating Least Square (ALS), cannot be easily applied to complex tensor decomposition or often lead to poor accuracy at convergence. We propose a new resolution algorithm, called VecHGrad, for accurate and efficient stochastic resolution over all existing tensor decomposition, specifically designed for complex decomposition. VecHGrad relies on gradient, Hessian-vector product and adaptive line search to ensure the convergence during optimization. Our experiments on five real-world data sets with the state-of-the-art deep learning gradient optimization models show that VecHGrad is capable of converging considerably faster because of its superior theoretical convergence rate per step. Therefore, VecHGrad targets as well deep learning optimizer algorithms. The experiments are performed for various tensor decomposition including CP, DEDICOM and PARATUCK2. Although it involves a slightly more complex update rule, VecHGrad's runtime is similar in practice to that of gradient methods such as SGD, Adam or RMSProp.