Experimental Demonstration of Online Learning-Based Concept Drift Adaptation for Failure Detection in Optical Networks

We present a novel online learning-based approach for concept drift adaptation in optical network failure detection, achieving up to a 70% improvement in performance over conventional static models while maintaining low latency.

Efficient and Robust Semantic Image Communication via Stable Cascade

Diffusion Model (DM) based Semantic Image Communication (SIC) systems face significant challenges, such as slow inference speed and generation randomness, that limit their reliability and practicality. To overcome these issues, we propose a novel SIC framework inspired by Stable Cascade, where extremely compact latent image embeddings are used as conditioning to the diffusion process. Our approach drastically reduces the data transmission overhead, compressing the transmitted embedding to just 0.29% of the original image size. It outperforms three benchmark approaches - the diffusion SIC model conditioned on segmentation maps (GESCO), the recent Stable Diffusion (SD)-based SIC framework (Img2Img-SC), and the conventional JPEG2000 + LDPC coding - by achieving superior reconstruction quality under noisy channel conditions, as validated across multiple metrics. Notably, it also delivers significant computational efficiency, enabling over 3x faster reconstruction for 512 x 512 images and more than 16x faster for 1024 x 1024 images as compared to the approach adopted in Img2Img-SC.

FPGA Implementation of Low-Power Multiplierless Pre-Processing Free Chromatic Dispersion Equalizer

We present a novel time-domain chromatic dispersion equalizer, implemented on FPGA, eliminating pre-processing and multipliers, achieving up to 54.3% energy savings over 80-1280 km with a simple, low-power design.

Geometric Clustering for Hardware-Efficient Implementation of Chromatic Dispersion Compensation

Power efficiency remains a significant challenge in modern optical fiber communication systems, driving efforts to reduce the computational complexity of digital signal processing, particularly in chromatic dispersion compensation (CDC) algorithms. While various strategies for complexity reduction have been proposed, many lack the necessary hardware implementation to validate their benefits. This paper provides a theoretical analysis of the tap overlapping effect in CDC filters for coherent receivers, introduces a novel Time-Domain Clustered Equalizer (TDCE) technique based on this concept, and presents a Field-Programmable Gate Array (FPGA) implementation for validation. We developed an innovative parallelization method for TDCE, implementing it in hardware for fiber lengths up to 640 km. A fair comparison with the state-of-the-art frequency domain equalizer (FDE) under identical conditions is also conducted. Our findings highlight that implementation strategies, including parallelization and memory management, are as crucial as computational complexity in determining hardware complexity and energy efficiency. The proposed TDCE hardware implementation achieves up to 70.7\% energy savings and 71.4\% multiplier usage savings compared to FDE, despite its higher computational complexity.

Artificial Neural Networks for Photonic Applications: From Algorithms to Implementation

This tutorial-review on applications of artificial neural networks in photonics targets a broad audience, ranging from optical research and engineering communities to computer science and applied mathematics. We focus here on the research areas at the interface between these disciplines, attempting to find the right balance between technical details specific to each domain and overall clarity. First, we briefly recall key properties and peculiarities of some core neural network types, which we believe are the most relevant to photonics, also linking the layer's theoretical design to some photonics hardware realizations. After that, we elucidate the question of how to fine-tune the selected model's design to perform the required task with optimized accuracy. Then, in the review part, we discuss recent developments and progress for several selected applications of neural networks in photonics, including multiple aspects relevant to optical communications, imaging, sensing, and the design of new materials and lasers. In the following section, we put a special emphasis on how to accurately evaluate the complexity of neural networks in the context of the transition from algorithms to hardware implementation. The introduced complexity characteristics are used to analyze the applications of neural networks in optical communications, as a specific, albeit highly important example, comparing those with some benchmark signal processing methods. We combine the description of the well-known model compression strategies used in machine learning, with some novel techniques introduced recently in optical applications of neural networks. It is important to stress that although our focus in this tutorial-review is on photonics, we believe that the methods and techniques presented here can be handy in a much wider range of scientific and engineering applications.

Multi-Task Learning to Enhance Generazability of Neural Network Equalizers in Coherent Optical Systems

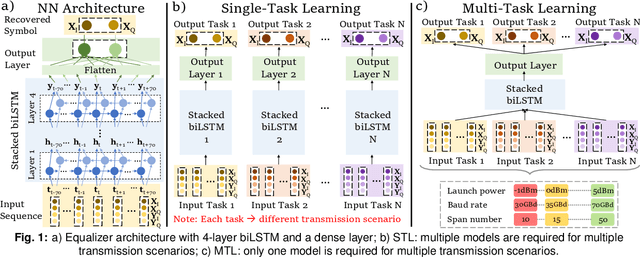
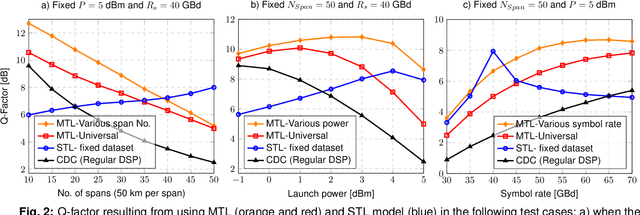
For the first time, multi-task learning is proposed to improve the flexibility of NN-based equalizers in coherent systems. A "single" NN-based equalizer improves Q-factor by up to 4 dB compared to CDC, without re-training, even with variations in launch power, symbol rate, or transmission distance.

Hardware Realization of Nonlinear Activation Functions for NN-based Optical Equalizers

To reduce the complexity of the hardware implementation of neural network-based optical channel equalizers, we demonstrate that the performance of the biLSTM equalizer with approximated activation functions is close to that of the original model.

Implementing Neural Network-Based Equalizers in a Coherent Optical Transmission System Using Field-Programmable Gate Arrays

In this work, we demonstrate the offline FPGA realization of both recurrent and feedforward neural network (NN)-based equalizers for nonlinearity compensation in coherent optical transmission systems. First, we present a realization pipeline showing the conversion of the models from Python libraries to the FPGA chip synthesis and implementation. Then, we review the main alternatives for the hardware implementation of nonlinear activation functions. The main results are divided into three parts: a performance comparison, an analysis of how activation functions are implemented, and a report on the complexity of the hardware. The performance in Q-factor is presented for the cases of bidirectional long-short-term memory coupled with convolutional NN (biLSTM + CNN) equalizer, CNN equalizer, and standard 1-StpS digital back-propagation (DBP) for the simulation and experiment propagation of a single channel dual-polarization (SC-DP) 16QAM at 34 GBd along 17x70km of LEAF. The biLSTM+CNN equalizer provides a similar result to DBP and a 1.7 dB Q-factor gain compared with the chromatic dispersion compensation baseline in the experimental dataset. After that, we assess the Q-factor and the impact of hardware utilization when approximating the activation functions of NN using Taylor series, piecewise linear, and look-up table (LUT) approximations. We also show how to mitigate the approximation errors with extra training and provide some insights into possible gradient problems in the LUT approximation. Finally, to evaluate the complexity of hardware implementation to achieve 400G throughput, fixed-point NN-based equalizers with approximated activation functions are developed and implemented in an FPGA.

Knowledge Distillation Applied to Optical Channel Equalization: Solving the Parallelization Problem of Recurrent Connection

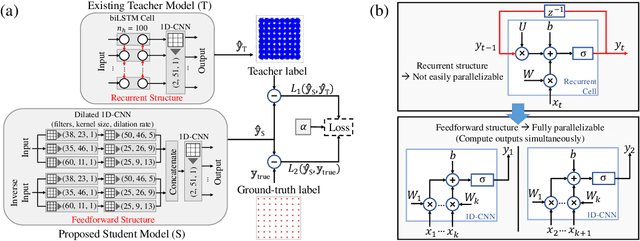
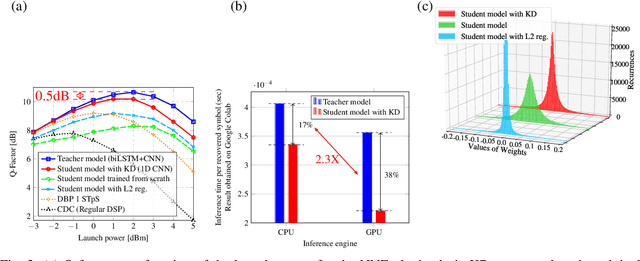
To circumvent the non-parallelizability of recurrent neural network-based equalizers, we propose knowledge distillation to recast the RNN into a parallelizable feedforward structure. The latter shows 38\% latency decrease, while impacting the Q-factor by only 0.5dB.

Reducing Computational Complexity of Neural Networks in Optical Channel Equalization: From Concepts to Implementation

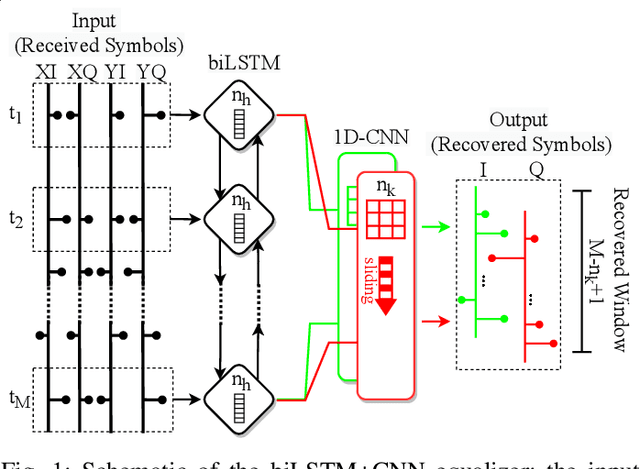
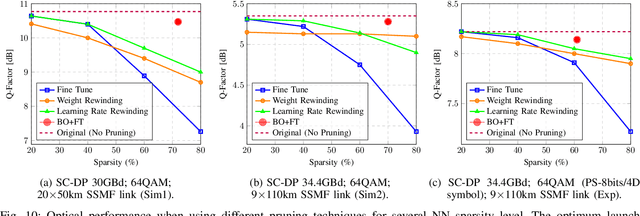
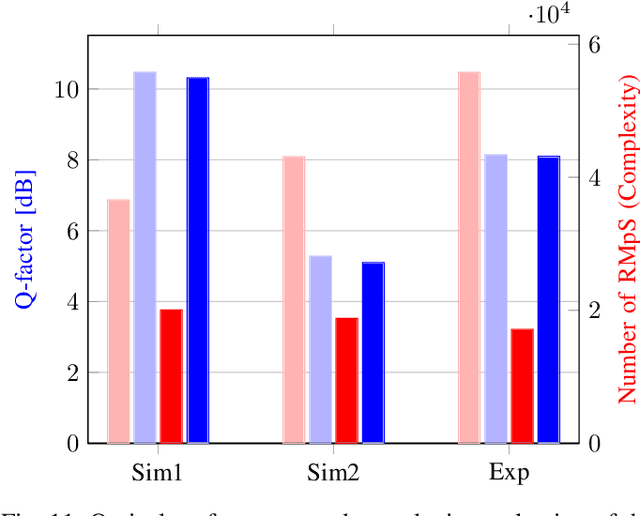
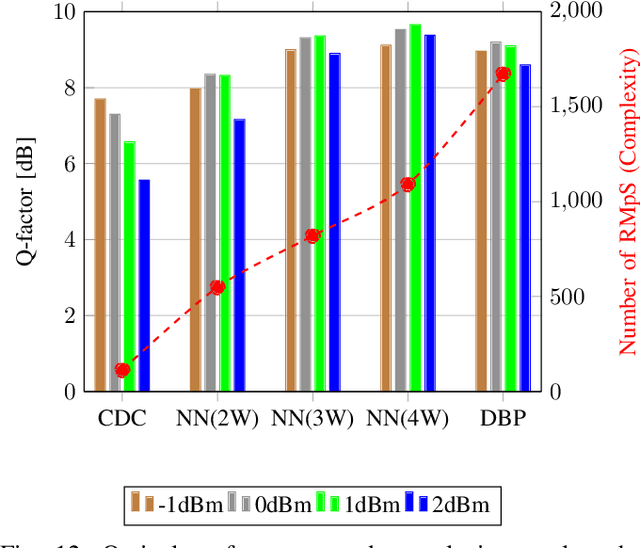
In this paper, a new methodology is proposed that allows for the low-complexity development of neural network (NN) based equalizers for the mitigation of impairments in high-speed coherent optical transmission systems. In this work, we provide a comprehensive description and comparison of various deep model compression approaches that have been applied to feed-forward and recurrent NN designs. Additionally, we evaluate the influence these strategies have on the performance of each NN equalizer. Quantization, weight clustering, pruning, and other cutting-edge strategies for model compression are taken into consideration. In this work, we propose and evaluate a Bayesian optimization-assisted compression, in which the hyperparameters of the compression are chosen to simultaneously reduce complexity and improve performance. In conclusion, the trade-off between the complexity of each compression approach and its performance is evaluated by utilizing both simulated and experimental data in order to complete the analysis. By utilizing optimal compression approaches, we show that it is possible to design an NN-based equalizer that is simpler to implement and has better performance than the conventional digital back-propagation (DBP) equalizer with only one step per span. This is accomplished by reducing the number of multipliers used in the NN equalizer after applying the weighted clustering and pruning algorithms. Furthermore, we demonstrate that an equalizer based on NN can also achieve superior performance while still maintaining the same degree of complexity as the full electronic chromatic dispersion compensation block. We conclude our analysis by highlighting open questions and existing challenges, as well as possible future research directions.