Implementing Neural Network-Based Equalizers in a Coherent Optical Transmission System Using Field-Programmable Gate Arrays

In this work, we demonstrate the offline FPGA realization of both recurrent and feedforward neural network (NN)-based equalizers for nonlinearity compensation in coherent optical transmission systems. First, we present a realization pipeline showing the conversion of the models from Python libraries to the FPGA chip synthesis and implementation. Then, we review the main alternatives for the hardware implementation of nonlinear activation functions. The main results are divided into three parts: a performance comparison, an analysis of how activation functions are implemented, and a report on the complexity of the hardware. The performance in Q-factor is presented for the cases of bidirectional long-short-term memory coupled with convolutional NN (biLSTM + CNN) equalizer, CNN equalizer, and standard 1-StpS digital back-propagation (DBP) for the simulation and experiment propagation of a single channel dual-polarization (SC-DP) 16QAM at 34 GBd along 17x70km of LEAF. The biLSTM+CNN equalizer provides a similar result to DBP and a 1.7 dB Q-factor gain compared with the chromatic dispersion compensation baseline in the experimental dataset. After that, we assess the Q-factor and the impact of hardware utilization when approximating the activation functions of NN using Taylor series, piecewise linear, and look-up table (LUT) approximations. We also show how to mitigate the approximation errors with extra training and provide some insights into possible gradient problems in the LUT approximation. Finally, to evaluate the complexity of hardware implementation to achieve 400G throughput, fixed-point NN-based equalizers with approximated activation functions are developed and implemented in an FPGA.

Reducing Computational Complexity of Neural Networks in Optical Channel Equalization: From Concepts to Implementation

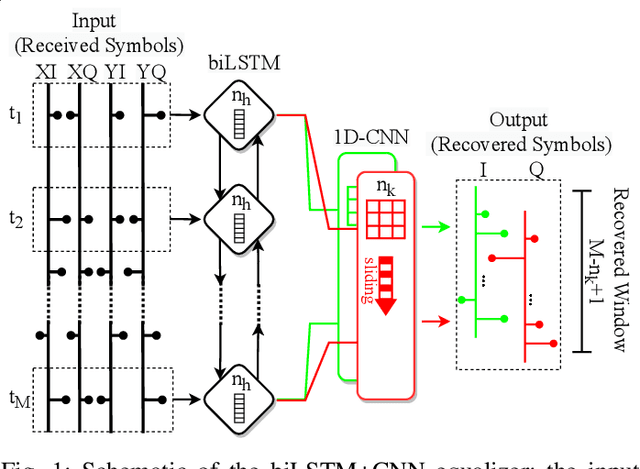
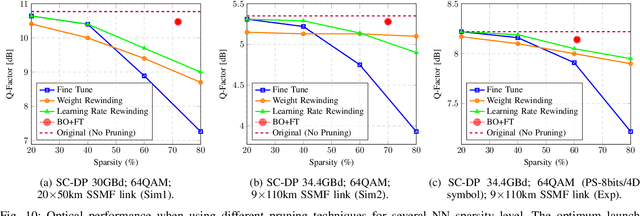
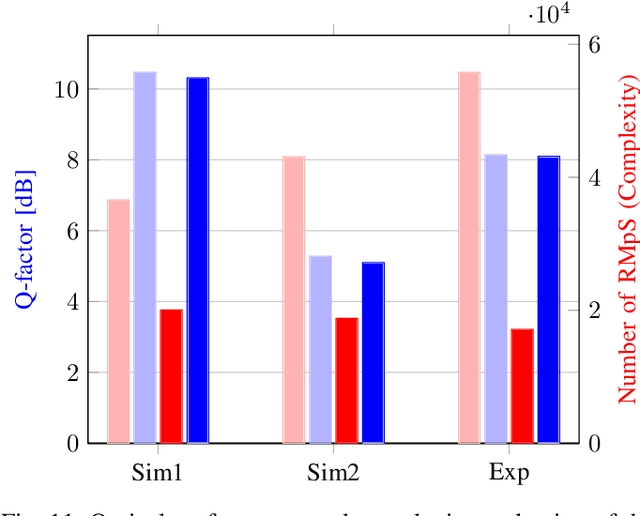
In this paper, a new methodology is proposed that allows for the low-complexity development of neural network (NN) based equalizers for the mitigation of impairments in high-speed coherent optical transmission systems. In this work, we provide a comprehensive description and comparison of various deep model compression approaches that have been applied to feed-forward and recurrent NN designs. Additionally, we evaluate the influence these strategies have on the performance of each NN equalizer. Quantization, weight clustering, pruning, and other cutting-edge strategies for model compression are taken into consideration. In this work, we propose and evaluate a Bayesian optimization-assisted compression, in which the hyperparameters of the compression are chosen to simultaneously reduce complexity and improve performance. In conclusion, the trade-off between the complexity of each compression approach and its performance is evaluated by utilizing both simulated and experimental data in order to complete the analysis. By utilizing optimal compression approaches, we show that it is possible to design an NN-based equalizer that is simpler to implement and has better performance than the conventional digital back-propagation (DBP) equalizer with only one step per span. This is accomplished by reducing the number of multipliers used in the NN equalizer after applying the weighted clustering and pruning algorithms. Furthermore, we demonstrate that an equalizer based on NN can also achieve superior performance while still maintaining the same degree of complexity as the full electronic chromatic dispersion compensation block. We conclude our analysis by highlighting open questions and existing challenges, as well as possible future research directions.

Towards FPGA Implementation of Neural Network-Based Nonlinearity Mitigation Equalizers in Coherent Optical Transmission Systems

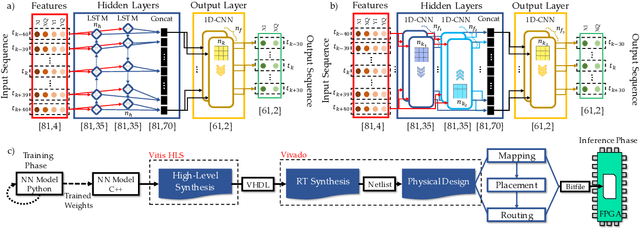
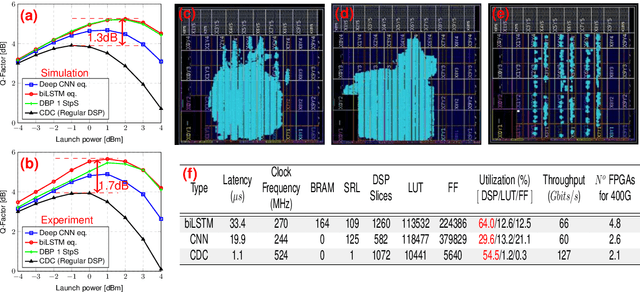
For the first time, recurrent and feedforward neural network-based equalizers for nonlinearity compensation are implemented in an FPGA, with a level of complexity comparable to that of a dispersion equalizer. We demonstrate that the NN-based equalizers can outperform a 1 step-per-span DBP.

Domain Adaptation: the Key Enabler of Neural Network Equalizers in Coherent Optical Systems

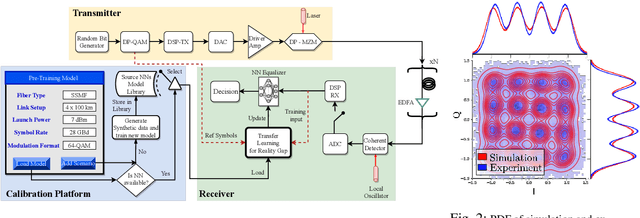
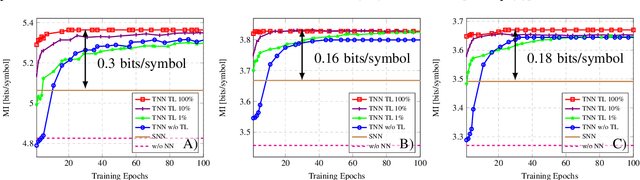
We introduce the domain adaptation and randomization approach for calibrating neural network-based equalizers for real transmissions, using synthetic data. The approach renders up to 99\% training process reduction, which we demonstrate in three experimental setups.

Experimental Evaluation of Computational Complexity for Different Neural Network Equalizers in Optical Communications

Addressing the neural network-based optical channel equalizers, we quantify the trade-off between their performance and complexity by carrying out the comparative analysis of several neural network architectures, presenting the results for TWC and SSMF set-ups.

Experimental Study of Deep Neural Network Equalizers Performance in Optical Links

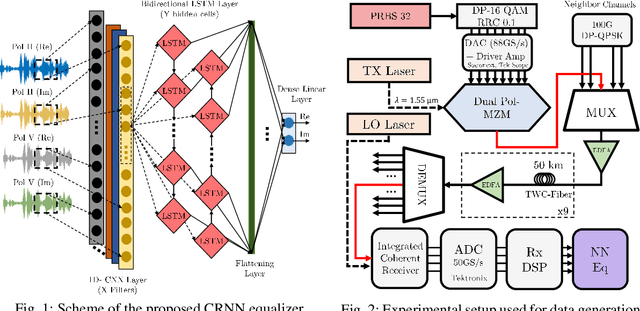
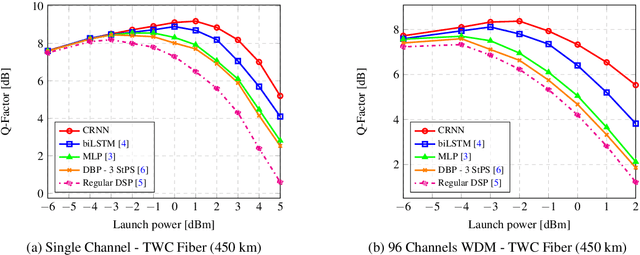
We propose a convolutional-recurrent channel equalizer and experimentally demonstrate 1dB Q-factor improvement both in single-channel and 96 x WDM, DP-16QAM transmission over 450km of TWC fiber. The new equalizer outperforms previous NN-based approaches and a 3-steps-per-span DBP.

Performance versus Complexity Study of Neural Network Equalizers in Coherent Optical Systems

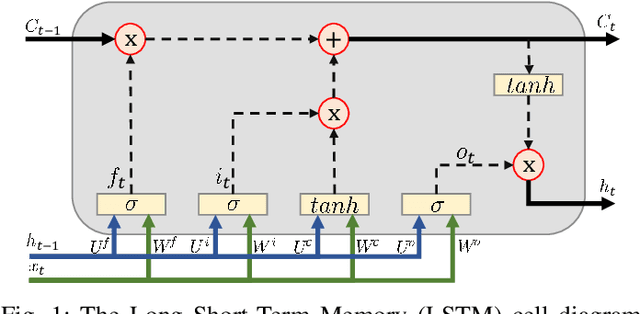
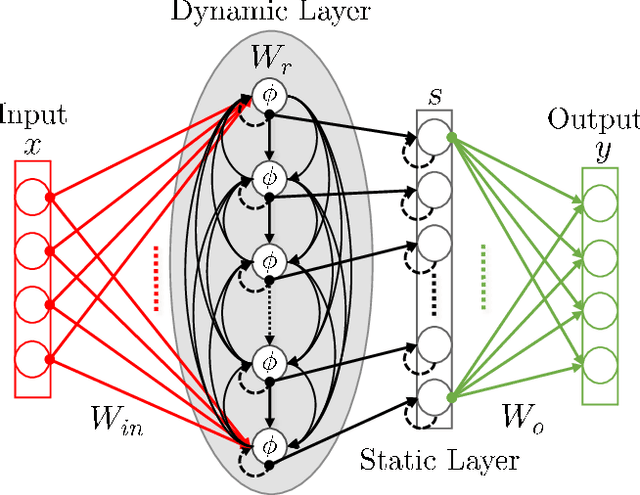
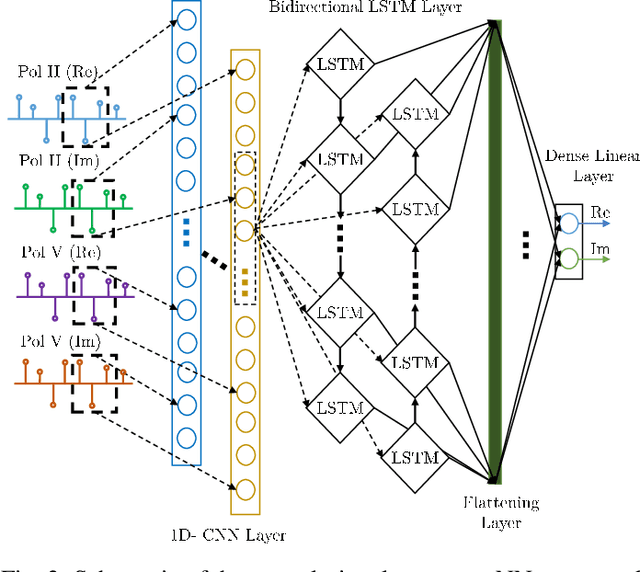
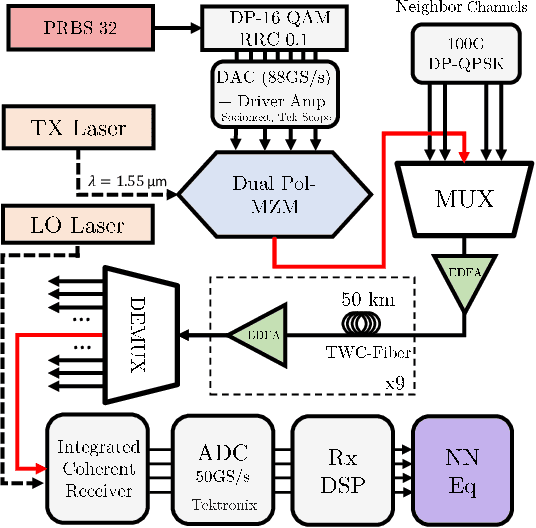
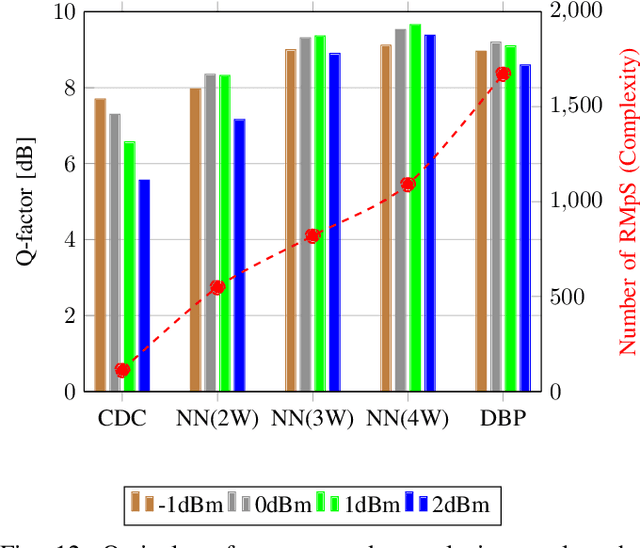
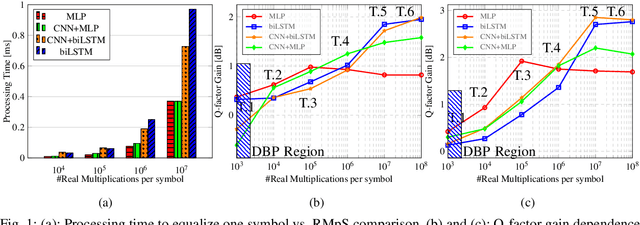
We present the results of the comparative analysis of the performance versus complexity for several types of artificial neural networks (NNs) used for nonlinear channel equalization in coherent optical communication systems. The comparison has been carried out using an experimental set-up with transmission dominated by the Kerr nonlinearity and component imperfections. For the first time, we investigate the application to the channel equalization of the convolution layer (CNN) in combination with a bidirectional long short-term memory (biLSTM) layer and the design combining CNN with a multi-layer perceptron. Their performance is compared with the one delivered by the previously proposed NN equalizer models: one biLSTM layer, three-dense-layer perceptron, and the echo state network. Importantly, all architectures have been initially optimized by a Bayesian optimizer. We present the derivation of the computational complexity associated with each NN type -- in terms of real multiplications per symbol so that these results can be applied to a large number of communication systems. We demonstrated that in the specific considered experimental system the convolutional layer coupled with the biLSTM (CNN+biLSTM) provides the highest Q-factor improvement compared to the reference linear chromatic dispersion compensation (2.9 dB improvement). We examine the trade-off between the computational complexity and performance of all equalizers and demonstrate that the CNN+biLSTM is the best option when the computational complexity is not constrained, while when we restrict the complexity to lower levels, the three-layer perceptron provides the best performance. Our complexity analysis for different NNs is generic and can be applied in a wide range of physical and engineering systems.