Low-complexity Samples versus Symbols-based Neural Network Receiver for Channel Equalization

Low-complexity neural networks (NNs) have successfully been applied for digital signal processing (DSP) in short-reach intensity-modulated directly detected optical links, where chromatic dispersion-induced impairments significantly limit the transmission distance. The NN-based equalizers are usually optimized independently from other DSP components, such as matched filtering. This approach may result in lower equalization performance. Alternatively, optimizing a NN equalizer to perform functionalities of multiple DSP blocks may increase transmission reach while keeping the complexity low. In this work, we propose a low-complexity NN that performs samples-to-symbol equalization, meaning that the NN-based equalizer includes match filtering and downsampling. We compare it to a samples-to-sample equalization approach followed by match filtering and downsampling in terms of performance and computational complexity. Both approaches are evaluated using three different types of NNs combined with optical preprocessing. We numerically and experimentally show that the proposed samples-to-symbol equalization approach applied for 32 GBd on-off keying (OOK) signals outperforms the samples-domain alternative keeping the computational complexity low. Additionally, the different types of NN-based equalizers are compared in terms of performance with respect to computational complexity.

Reservoir Computing-based Multi-Symbol Equalization for PAM 4 Short-reach Transmission

We propose spectrum-sliced reservoir computer-based (RC) multi-symbol equalization for 32-GBd PAM4 transmission. RC with 17 symbols at the output achieves an order of magnitude reduction in multiplications/symbol versus single output case while maintaining simple training.

Neural networks based post-equalization in coherent optical systems: regression versus classification

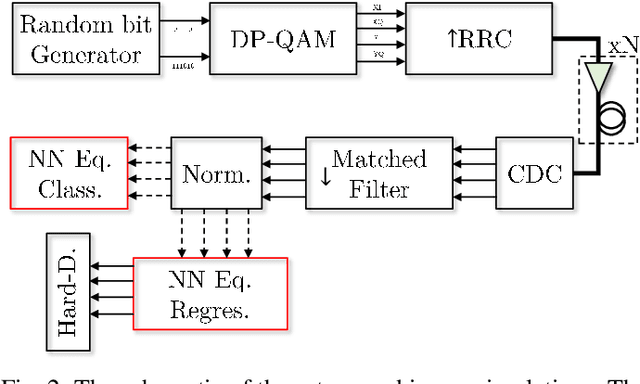
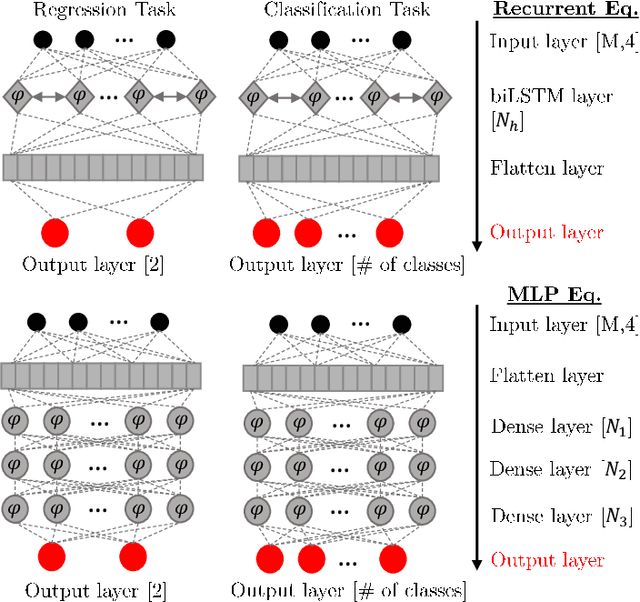
In this paper, we address the question of which type of predictive modeling, classification, or regression, fits better the task of equalization using neural networks (NN) based post-processing in coherent optical communication, where the transmission channel is nonlinear and dispersive. For the first time, we presented some possible drawbacks in using each type of predictive task in a machine learning context for the nonlinear channel equalization problem. We studied two types of equalizers based on the feed-forward and recurrent neural networks over several different transmission scenarios, in linear and nonlinear regimes of the optical channel. We observed in all those cases that the training based on regression results in faster convergence and finally a superior performance, in terms of Q-factor and achievable information rate.

Experimental Evaluation of Computational Complexity for Different Neural Network Equalizers in Optical Communications

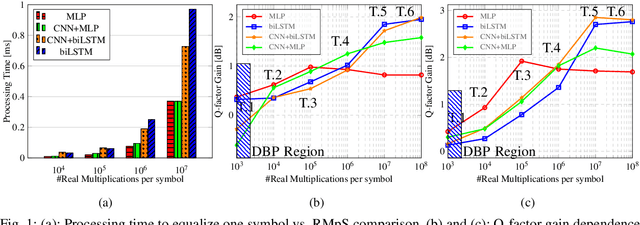
Addressing the neural network-based optical channel equalizers, we quantify the trade-off between their performance and complexity by carrying out the comparative analysis of several neural network architectures, presenting the results for TWC and SSMF set-ups.

Experimental Study of Deep Neural Network Equalizers Performance in Optical Links

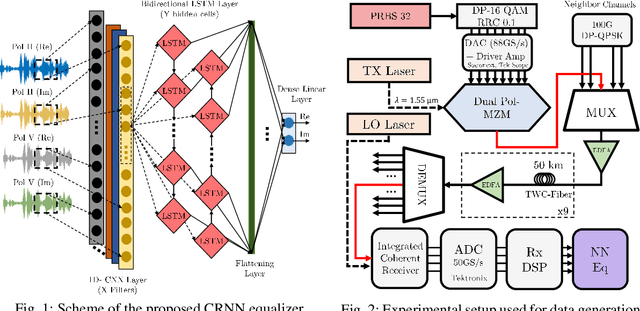
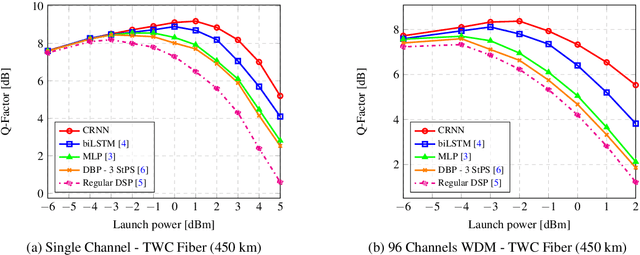
We propose a convolutional-recurrent channel equalizer and experimentally demonstrate 1dB Q-factor improvement both in single-channel and 96 x WDM, DP-16QAM transmission over 450km of TWC fiber. The new equalizer outperforms previous NN-based approaches and a 3-steps-per-span DBP.

Performance versus Complexity Study of Neural Network Equalizers in Coherent Optical Systems

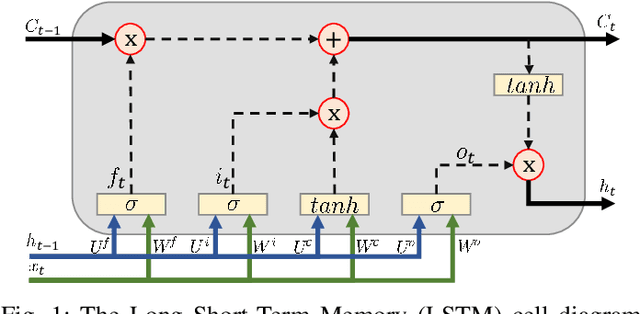
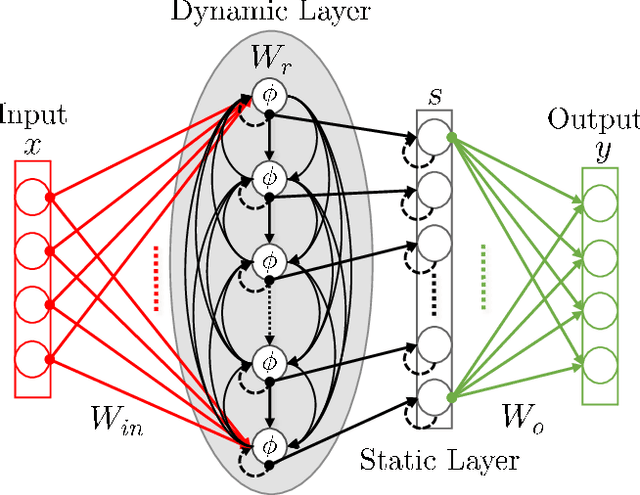
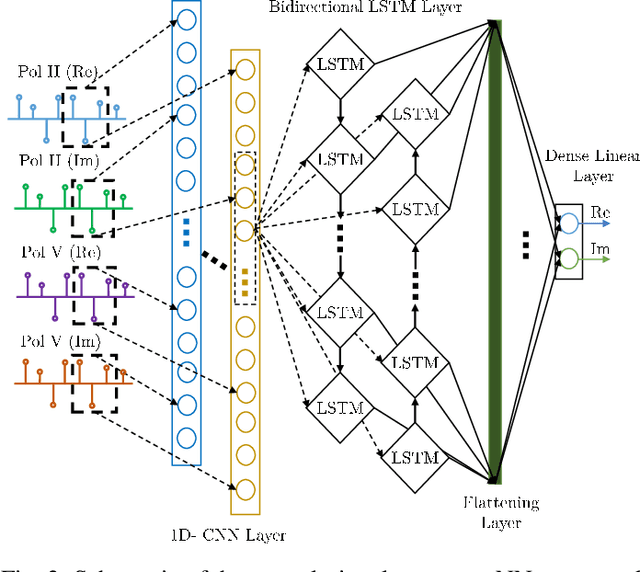
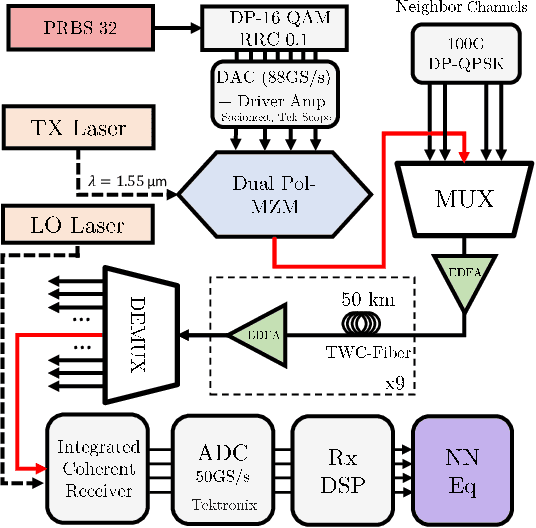
We present the results of the comparative analysis of the performance versus complexity for several types of artificial neural networks (NNs) used for nonlinear channel equalization in coherent optical communication systems. The comparison has been carried out using an experimental set-up with transmission dominated by the Kerr nonlinearity and component imperfections. For the first time, we investigate the application to the channel equalization of the convolution layer (CNN) in combination with a bidirectional long short-term memory (biLSTM) layer and the design combining CNN with a multi-layer perceptron. Their performance is compared with the one delivered by the previously proposed NN equalizer models: one biLSTM layer, three-dense-layer perceptron, and the echo state network. Importantly, all architectures have been initially optimized by a Bayesian optimizer. We present the derivation of the computational complexity associated with each NN type -- in terms of real multiplications per symbol so that these results can be applied to a large number of communication systems. We demonstrated that in the specific considered experimental system the convolutional layer coupled with the biLSTM (CNN+biLSTM) provides the highest Q-factor improvement compared to the reference linear chromatic dispersion compensation (2.9 dB improvement). We examine the trade-off between the computational complexity and performance of all equalizers and demonstrate that the CNN+biLSTM is the best option when the computational complexity is not constrained, while when we restrict the complexity to lower levels, the three-layer perceptron provides the best performance. Our complexity analysis for different NNs is generic and can be applied in a wide range of physical and engineering systems.