Calibration Strategies for Robust Causal Estimation: Theoretical and Empirical Insights on Propensity Score Based Estimators

The partitioning of data for estimation and calibration critically impacts the performance of propensity score based estimators like inverse probability weighting (IPW) and double/debiased machine learning (DML) frameworks. We extend recent advances in calibration techniques for propensity score estimation, improving the robustness of propensity scores in challenging settings such as limited overlap, small sample sizes, or unbalanced data. Our contributions are twofold: First, we provide a theoretical analysis of the properties of calibrated estimators in the context of DML. To this end, we refine existing calibration frameworks for propensity score models, with a particular emphasis on the role of sample-splitting schemes in ensuring valid causal inference. Second, through extensive simulations, we show that calibration reduces variance of inverse-based propensity score estimators while also mitigating bias in IPW, even in small-sample regimes. Notably, calibration improves stability for flexible learners (e.g., gradient boosting) while preserving the doubly robust properties of DML. A key insight is that, even when methods perform well without calibration, incorporating a calibration step does not degrade performance, provided that an appropriate sample-splitting approach is chosen.

Collusion Detection with Graph Neural Networks

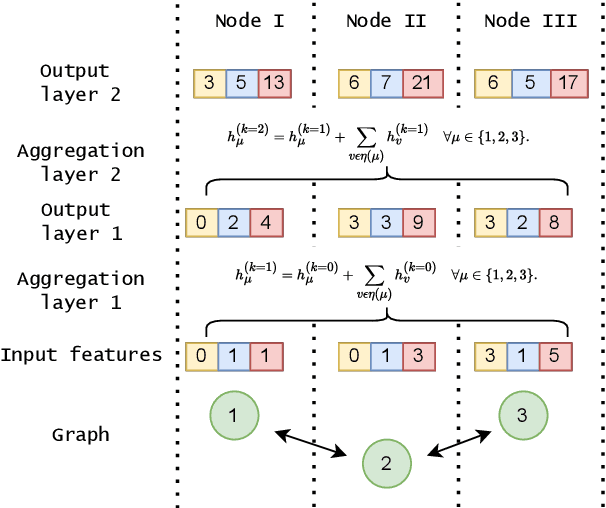
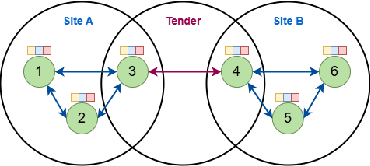
Collusion is a complex phenomenon in which companies secretly collaborate to engage in fraudulent practices. This paper presents an innovative methodology for detecting and predicting collusion patterns in different national markets using neural networks (NNs) and graph neural networks (GNNs). GNNs are particularly well suited to this task because they can exploit the inherent network structures present in collusion and many other economic problems. Our approach consists of two phases: In Phase I, we develop and train models on individual market datasets from Japan, the United States, two regions in Switzerland, Italy, and Brazil, focusing on predicting collusion in single markets. In Phase II, we extend the models' applicability through zero-shot learning, employing a transfer learning approach that can detect collusion in markets in which training data is unavailable. This phase also incorporates out-of-distribution (OOD) generalization to evaluate the models' performance on unseen datasets from other countries and regions. In our empirical study, we show that GNNs outperform NNs in detecting complex collusive patterns. This research contributes to the ongoing discourse on preventing collusion and optimizing detection methodologies, providing valuable guidance on the use of NNs and GNNs in economic applications to enhance market fairness and economic welfare.

Uniform Inference in High-Dimensional Generalized Additive Models

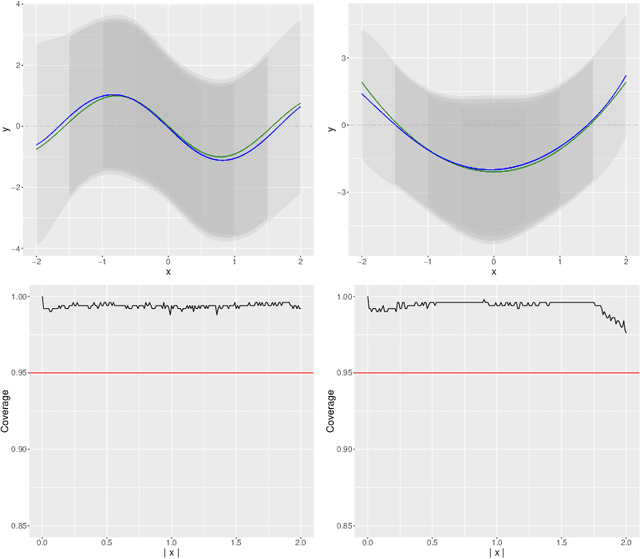
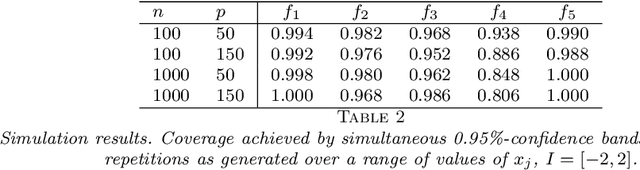
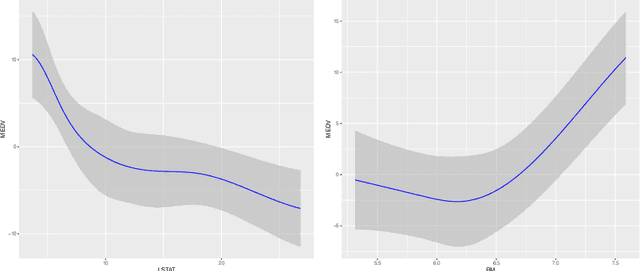
We develop a method for uniform valid confidence bands of a nonparametric component $f_1$ in the general additive model $Y=f_1(X_1)+\ldots + f_p(X_p) + \varepsilon$ in a high-dimensional setting. We employ sieve estimation and embed it in a high-dimensional Z-estimation framework allowing us to construct uniformly valid confidence bands for the first component $f_1$. As usual in high-dimensional settings where the number of regressors $p$ may increase with sample, a sparsity assumption is critical for the analysis. We also run simulations studies which show that our proposed method gives reliable results concerning the estimation properties and coverage properties even in small samples. Finally, we illustrate our procedure with an empirical application demonstrating the implementation and the use of the proposed method in practice.

Transformation Models in High-Dimensions

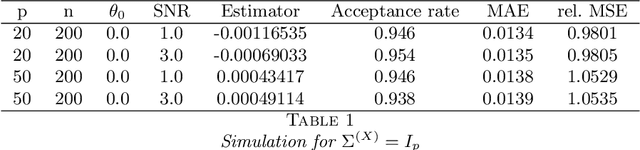
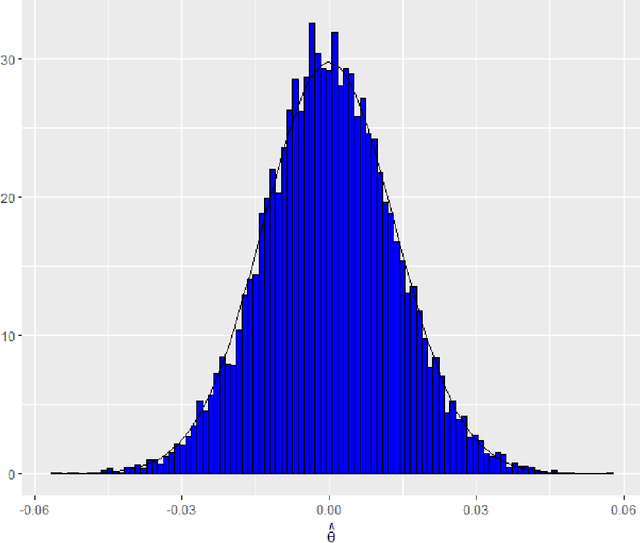
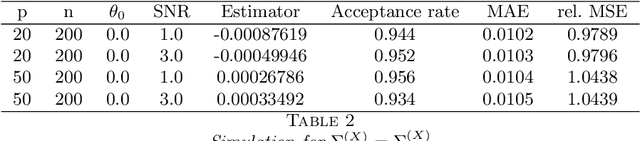
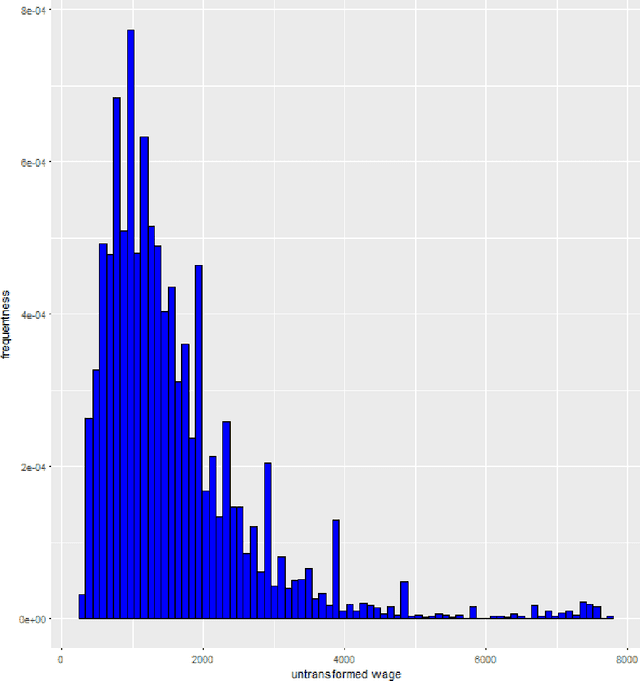
Transformation models are a very important tool for applied statisticians and econometricians. In many applications, the dependent variable is transformed so that homogeneity or normal distribution of the error holds. In this paper, we analyze transformation models in a high-dimensional setting, where the set of potential covariates is large. We propose an estimator for the transformation parameter and we show that it is asymptotically normally distributed using an orthogonalized moment condition where the nuisance functions depend on the target parameter. In a simulation study, we show that the proposed estimator works well in small samples. A common practice in labor economics is to transform wage with the log-function. In this study, we test if this transformation holds in CPS data from the United States.