Uniform Inference in High-Dimensional Generalized Additive Models

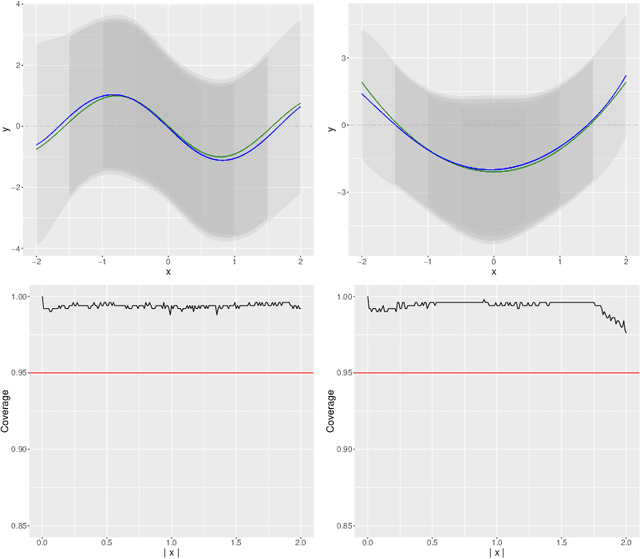
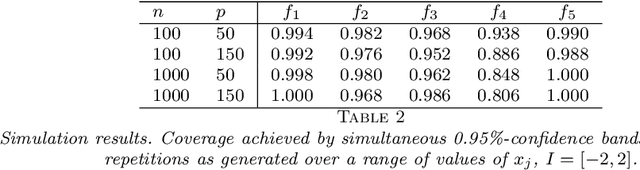
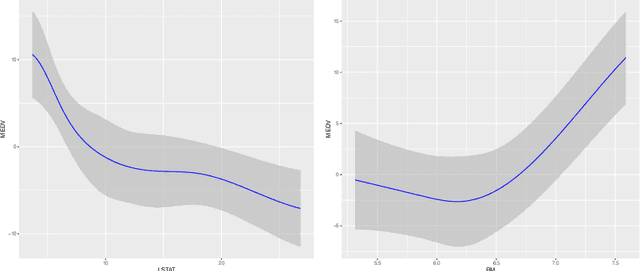
We develop a method for uniform valid confidence bands of a nonparametric component $f_1$ in the general additive model $Y=f_1(X_1)+\ldots + f_p(X_p) + \varepsilon$ in a high-dimensional setting. We employ sieve estimation and embed it in a high-dimensional Z-estimation framework allowing us to construct uniformly valid confidence bands for the first component $f_1$. As usual in high-dimensional settings where the number of regressors $p$ may increase with sample, a sparsity assumption is critical for the analysis. We also run simulations studies which show that our proposed method gives reliable results concerning the estimation properties and coverage properties even in small samples. Finally, we illustrate our procedure with an empirical application demonstrating the implementation and the use of the proposed method in practice.