Learning to Transfer: A Foliated Theory

Learning to transfer considers learning solutions to tasks in a such way that relevant knowledge can be transferred from known task solutions to new, related tasks. This is important for general learning, as well as for improving the efficiency of the learning process. While techniques for learning to transfer have been studied experimentally, we still lack a foundational description of the problem that exposes what related tasks are, and how relationships between tasks can be exploited constructively. In this work, we introduce a framework using the differential geometric theory of foliations that provides such a foundation.

GENNI: Visualising the Geometry of Equivalences for Neural Network Identifiability

We propose an efficient algorithm to visualise symmetries in neural networks. Typically, models are defined with respect to a parameter space, where non-equal parameters can produce the same input-output map. Our proposed method, GENNI, allows us to efficiently identify parameters that are functionally equivalent and then visualise the subspace of the resulting equivalence class. By doing so, we are now able to better explore questions surrounding identifiability, with applications to optimisation and generalizability, for commonly used or newly developed neural network architectures.

A Foliated View of Transfer Learning

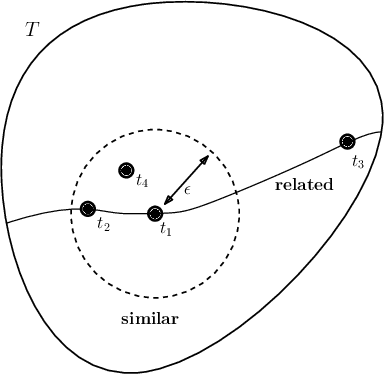
Transfer learning considers a learning process where a new task is solved by transferring relevant knowledge from known solutions to related tasks. While this has been studied experimentally, there lacks a foundational description of the transfer learning problem that exposes what related tasks are, and how they can be exploited. In this work, we present a definition for relatedness between tasks and identify foliations as a mathematical framework to represent such relationships.