Optimal Partial Graph Matching

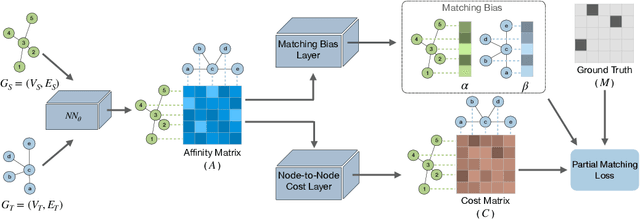
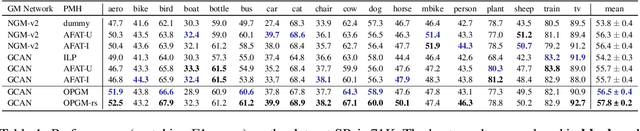
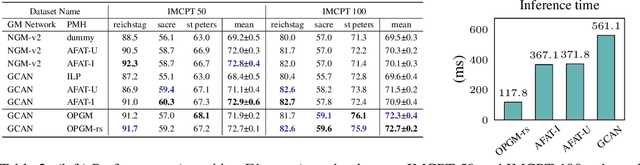
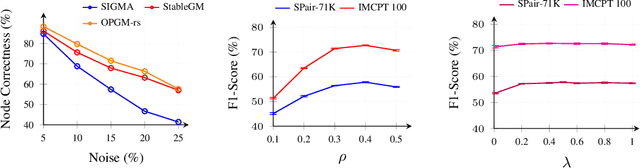
Partial graph matching addresses the limitations of traditional graph matching by allowing some nodes to remain unmatched, making it applicable to more complex scenarios. However, this flexibility introduces additional complexity, as both the subset of nodes to match and the optimal mapping must be determined. While recent studies have explored deep learning techniques for partial graph matching, a significant limitation remains: the absence of an optimization objective that fully captures the problem's intrinsic nature while enabling efficient solutions. In this paper, we propose a novel optimization framework for partial graph matching, inspired by optimal partial transport. Our approach formulates an objective that enables partial assignments while incorporating matching biases, using weighted total variation as the divergence function to guarantee optimal partial assignments. We employ the Hungarian algorithm to achieve efficient, exact solutions with cubic time complexity. Our contributions are threefold: (i) we introduce a robust optimization objective that balances matched and unmatched nodes; (ii) we establish a connection between partial graph matching and the linear sum assignment problem, enabling efficient solutions; (iii) we propose a deep graph matching architecture with a novel partial matching loss, providing an end-to-end solution. The empirical evaluations on standard graph matching benchmarks demonstrate the efficacy of the proposed approach.

Topological Deep Learning: A Review of an Emerging Paradigm

Topological data analysis (TDA) provides insight into data shape. The summaries obtained by these methods are principled global descriptions of multi-dimensional data whilst exhibiting stable properties such as robustness to deformation and noise. Such properties are desirable in deep learning pipelines but they are typically obtained using non-TDA strategies. This is partly caused by the difficulty of combining TDA constructs (e.g. barcode and persistence diagrams) with current deep learning algorithms. Fortunately, we are now witnessing a growth of deep learning applications embracing topologically-guided components. In this survey, we review the nascent field of topological deep learning by first revisiting the core concepts of TDA. We then explore how the use of TDA techniques has evolved over time to support deep learning frameworks, and how they can be integrated into different aspects of deep learning. Furthermore, we touch on TDA usage for analyzing existing deep models; deep topological analytics. Finally, we discuss the challenges and future prospects of topological deep learning.